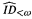Crossref Citations
This article has been cited by the following publications. This list is generated based on data provided by Crossref.
Avigad, Jeremy
and
Sommer, Richard
1997.
A Model-Theoretic Approach to Ordinal Analysis.
Bulletin of Symbolic Logic,
Vol. 3,
Issue. 1,
p.
17.
Avigad, Jeremy
1998.
Predicative functionals and an interpretation of ⌢ID<ω.
Annals of Pure and Applied Logic,
Vol. 92,
Issue. 1,
p.
1.
Avigad, Jeremy
and
Feferman, Solomon
1998.
Handbook of Proof Theory.
Vol. 137,
Issue. ,
p.
337.
Rüede, Christian
and
Strahm, Thomas
2002.
Intuitionistic Fixed Point Theories for Strictly Positive Operators.
MLQ,
Vol. 48,
Issue. 2,
p.
195.
Rüede, Christian
2003.
The proof-theoretic analysis of Σ11 transfinite dependent choice.
Annals of Pure and Applied Logic,
Vol. 122,
Issue. 1-3,
p.
195.
Jäger, Gerhard
2004.
An intensional fixed point theory over first order arithmetic.
Annals of Pure and Applied Logic,
Vol. 128,
Issue. 1-3,
p.
197.
Jäger, Gerhard
and
Probst, Dieter
2004.
Variation on a theme of Schütte.
Mathematical Logic Quarterly,
Vol. 50,
Issue. 3,
p.
258.
Probst, Dieter
2005.
On the relationship between fixed points and iteration in admissible set theory without foundation.
Archive for Mathematical Logic,
Vol. 44,
Issue. 5,
p.
561.
Rathjen, Michael
2011.
2010 European Summer Meeting of the Association for Symbolic Logic. Logic Colloquium '10.
The Bulletin of Symbolic Logic,
Vol. 17,
Issue. 2,
p.
272.
Sato, Kentaro
2014.
Forcing for hat inductive definitions in arithmetic.
Mathematical Logic Quarterly,
Vol. 60,
Issue. 4-5,
p.
314.
Sato, Kentaro
2015.
Full and hat inductive definitions are equivalent in NBG.
Archive for Mathematical Logic,
Vol. 54,
Issue. 1-2,
p.
75.
Arai, Toshiyasu
2015.
Intuitionistic fixed point theories over set theories.
Archive for Mathematical Logic,
Vol. 54,
Issue. 5-6,
p.
531.
Feferman, Solomon
2016.
Advances in Proof Theory.
Vol. 28,
Issue. ,
p.
269.
Strahm, Thomas
2017.
Logic Colloquium '98.
p.
449.
Jäger, Gerhard
2017.
Logic Colloquium 2000.
p.
272.
Sato, Kentaro
2020.
Elementary inductive dichotomy: Separation of open and clopen determinacies with infinite alternatives.
Annals of Pure and Applied Logic,
Vol. 171,
Issue. 3,
p.
102754.
Arai, Toshiyasu
2020.
Ordinal Analysis with an Introduction to Proof Theory.
p.
175.
Bärtschi, Michael
and
Jäger, Gerhard
2020.
The Legacy of Kurt Schütte.
p.
103.
Sato, Kentaro
2022.
Bounded inductive dichotomy: separation of open and clopen determinacies with finite alternatives in constructive contexts.
Archive for Mathematical Logic,
Vol. 61,
Issue. 3-4,
p.
399.
Fujimoto, Kentaro
2023.
A few more dissimilarities between second-order arithmetic and set theory.
Archive for Mathematical Logic,
Vol. 62,
Issue. 1-2,
p.
147.