Crossref Citations
This article has been cited by the following publications. This list is generated based on data provided by
Crossref.
Herrmann, Eberhard
1989.
Logic, Methodology and Philosophy of Science VIII, Proceedings of the Eighth International Congress of Logic, Methodology and Philosophy of Science.
Vol. 126,
Issue. ,
p.
179.
Cholak, P.
Downey, R.
and
Stob, M.
1992.
Automorphisms of the lattice of recursively enumerable sets: promptly simple sets.
Transactions of the American Mathematical Society,
Vol. 332,
Issue. 2,
p.
555.
Cholak, Peter
1994.
The translation theorem.
Archive for Mathematical Logic,
Vol. 33,
Issue. 2,
p.
87.
Harrington, Leo
and
Soare, Robert
1996.
The Δ₃⁰-automorphism method and noninvariant classes of degrees.
Journal of the American Mathematical Society,
Vol. 9,
Issue. 3,
p.
617.
Harrington, Leo
and
Soare, Robert I.
1998.
Definable properties of the computably enumerable sets.
Annals of Pure and Applied Logic,
Vol. 94,
Issue. 1-3,
p.
97.
Soare, Robert I.
1999.
Handbook of Computability Theory.
Vol. 140,
Issue. ,
p.
199.
Cholak, Peter
and
Harrington, Leo
2007.
Extension theorems, orbits, and automorphisms of the computably enumerable sets.
Transactions of the American Mathematical Society,
Vol. 360,
Issue. 4,
p.
1759.
Cholak, Peter A.
Downey, Rodney
and
Harrington, Leo A.
2008.
The Complexity of Orbits of Computably Enumerable Sets.
Bulletin of Symbolic Logic,
Vol. 14,
Issue. 1,
p.
69.
Cholak, Peter
Downey, Rodney
and
Harrington, Leo
2008.
On the orbits of computably enumerable sets.
Journal of the American Mathematical Society,
Vol. 21,
Issue. 4,
p.
1105.
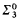 -definable isomorphism between their lattices of supersets. Lerman, Shore and Soare have shown that this is not true if one replaces
-definable isomorphism between their lattices of supersets. Lerman, Shore and Soare have shown that this is not true if one replaces 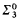 by
by 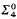 .
.

