Hostname: page-component-745bb68f8f-g4j75 Total loading time: 0 Render date: 2025-01-22T07:40:31.189Z Has data issue: false hasContentIssue false
  • English
  • Français

On the Hanf number of Souslin logic1

Published online by Cambridge University Press:  12 March 2014

John P. Burgess
John P. Burgess*
Affiliation:
Princeton University, Princeton, NJ 08540
Get access Rights & Permissions [Opens in a new window]

Abstract

We show it is consistent with ZFC that the Hanf number of Ellentuck's Souslin logic should be exactly .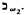

Type
Research Article
Information
The Journal of Symbolic Logic , Volume 43 , Issue 3 , September 1978 , pp. 568 - 571
Copyright
Copyright © Association for Symbolic Logic 1978

Access options

Get access to the full version of this content by using one of the access options below. (Log in options will check for institutional or personal access. Content may require purchase if you do not have access.)

Footnotes

1

Research supported by NSF MCS 76-10224.

References

BIBLIOGRAPHY

[1]Barwise, K. J., Absolute logics and L∞,ω, Annals of Mathematical Logic, vol. 4 (1972), pp. 309–349.CrossRefGoogle Scholar
[2]Burgess, J. P., Infinitary languages and descriptive set theory, Doctoral dissertation, University of California, Berkeley, 1974.Google Scholar
[3]Burgess, J. P., Descriptive set theory and infinitary languages, Proceedings of the Belgrade Symposium on Set Theory and Foundations of Mathematics (to appear).Google Scholar
[4]Ellentuck, E., Foundations of Souslin logic, this Journal, vol. 40 (1975), pp. 567–575.Google Scholar
[5]Keisler, H. J., Model theory for infinitary logic, North Holland, Amsterdam, 1971.Google Scholar
[6]Martin, D. A. and Solovay, R. M., Internal Cohen extensions, Annals of Mathematical Logic, vol. 2 (1970), pp. 143–178.CrossRefGoogle Scholar
[7]Vaught, R. L., Invariant sets in topology and logic, Fundamenta Mathematicae, vol. 82 (1974), pp. 270–294.CrossRefGoogle Scholar