Hostname: page-component-586b7cd67f-2plfb Total loading time: 0 Render date: 2024-11-25T07:10:48.446Z Has data issue: false hasContentIssue false
  • English
  • Français

On the degrees of unsolvability of modal predicate logics of provability

Published online by Cambridge University Press:  12 March 2014

Vann McGee
Vann McGee*
Affiliation:
Department of Philosophy, Rutgers University, New Brunswick, New Jersey 08903, E-mail: [email protected]
Get access Rights & Permissions [Opens in a new window]

Extract

The modal predicate logic of provability identifies the “□” of modal logic with the “Bew” of proof theory, so that, where “Bew” is a 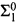formula representing, in the usual way, provability in a consistent, recursively axiomatized theory Γ extending Peano arithmetic (PA), an interpretation of a language for the modal predicate calculus is a map * which associates with each modal formula an arithmetical formula with the same free variables which commutes with the Boolean connectives and the quantifiers and which sets (□ϕ)* equal to Bew(⌈ϕ*⌉). Where Δ is an extension of PA (all the theories we discuss will be extensions of PA), MPL(Δ) will be the set of modal formulas ϕ such that, for every interpretation *, ϕ* is a theorem of Δ. Most of what is currently known about the modal predicate logic of provability consists in demonstrations that MPL(Δ) must be computationally highly complex. Thus Vardanyan [11] shows that, provided that Δ is 1-consistent and recursively axiomatizable, MPL(Δ) will be complete 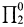, and Boolos and McGee [5] show that MPL({true arithmetical sentences}) is complete 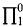in {true arithmetical sentences}. All of these results take as their starting point Artemov's demonstration in [1] that {true arithmetical sentences} is 1-reducible to MPL({true arithmetical sentences}).

The aim here is to consolidate these results by providing a general theorem which yields all the other results as special cases. These results provide a striking contrast with the situation in modal sentential logic (MSL); according to fundamental results of Solovay [8], provided Γ does not entail any 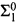falsehoods, MSL({true arithmetical sentences}) and MSL(PA) (which is the same as MSL(Γ)) are both decidable.

Type
Research Article
Information
The Journal of Symbolic Logic , Volume 59 , Issue 1 , March 1994 , pp. 253 - 261
Copyright
Copyright © Association for Symbolic Logic 1994

Access options

Get access to the full version of this content by using one of the access options below. (Log in options will check for institutional or personal access. Content may require purchase if you do not have access.)

References

REFERENCES

[1]Artemov, Sergei, Néarifmétičnost′ istinnostnyh prédkatnyh logik dokazuémosti, Doklady Académii Nauk SSSR, vol. 284 (1985), pp. 270–271; English translation by Elliott Mendelson, Nonarithmeticity of truth predicate logics of provability, Soviet Mathematics Doklady, vol. 32 (1986), pp. 403–405.Google Scholar
[2]Artemov, Sergei, Numéričéski korréktyné logiki dokazuémosti, Doklady Akadémii Nauk SSSR, vol. 290 (1986), pp. 1289–1292; English translation by Elliott Mendelson, Numerically Correct Provability Logics, Soviet Mathematics Doklady, vol. 34 (1987), pp. 384–387.Google Scholar
[3]Artemov, Sergei and Dzhaparidze, Giorgie, Finite Kripke models and predicate logics of provability, this Journal, vol. 55 (1990), pp. 1990–1998.Google Scholar
[4]Boolos, George, The logic of provability, Cambridge University Press (to appear).CrossRefGoogle Scholar
[5]Boolos, George and McGee, Vann, The degree of the set of sentences of predicate provability logic that are true under every interpretation, this Journal, vol. 52 (1987), pp. 165–171.Google Scholar
[6]Rosser, John Barkley, Extensions of some theorems of Gödel and Church, this Journal, vol. 1 (1936), pp. 87–91.Google Scholar
[7]Soare, Robert I., Recursively enumerable sets and degrees, Springer-Verlag, Berlin, 1987.CrossRefGoogle Scholar
[8]Solovay, Robert M., Provability interpretations of modal logic, Israel Journal of Mathematics, vol. 25 (1976), pp. 287–304.CrossRefGoogle Scholar
[9]Tarski, Alfred, Der Warheitsbegriff in den Formalisierten Sprachen, Studia Logica, vol. 1 (1935), pp. 261–405; English translation by J. H. Woodger, The concept of truth in formalized languages, in Tarski's, Logic, semantics, metamathematics, 2nd edition, Alfred Tarski, Hackett, Indianapolis, 1983, pp. 152–278.Google Scholar
[10]Tennenbaum, Stanley, Non-archimedean models for arithmetic, Notices of the American Mathematical Society, vol. 6 (1959), p. 207.Google Scholar
[11]Vardanyan, V. A., Arifmétiˇéskaá solžnost′ prédikatnyh logik dokazuémosti i ih fragméntov, Doklady Akadémii Nauk SSSR, vol. 288 (1986), pp. 11–14; English translation by Elliott Mendelson, Arithmetic complexity of predicate logics of provability and their fragments, Soviet Mathematics Doklady, vol. 33 (1987), pp. 569–572.Google Scholar
[12]Vaught, Robert L., Axiomatizability by a schema, this Journal, vol. 32 (1967), pp. 473–479.Google Scholar