No CrossRef data available.
Article contents
ON THE DECIDABILITY OF THE 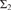 ${{\rm{\Sigma }}_2}$ THEORIES OF THE ARITHMETIC AND HYPERARITHMETIC DEGREES AS UPPERSEMILATTICES
${{\rm{\Sigma }}_2}$ THEORIES OF THE ARITHMETIC AND HYPERARITHMETIC DEGREES AS UPPERSEMILATTICES
Published online by Cambridge University Press: 09 January 2018
Abstract
We establish the decidability of the  ${{\rm{\Sigma }}_2}$ theory of both the arithmetic and hyperarithmetic degrees in the language of uppersemilattices, i.e., the language with ≤, 0 , and
${{\rm{\Sigma }}_2}$ theory of both the arithmetic and hyperarithmetic degrees in the language of uppersemilattices, i.e., the language with ≤, 0 , and  $\sqcup$. This is achieved by using Kumabe-Slaman forcing, along with other known results, to show given finite uppersemilattices
$\sqcup$. This is achieved by using Kumabe-Slaman forcing, along with other known results, to show given finite uppersemilattices 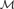 ${\cal M}$ and
${\cal M}$ and 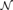 ${\cal N}$, where
${\cal N}$, where 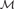 ${\cal M}$ is a subuppersemilattice of
${\cal M}$ is a subuppersemilattice of 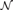 ${\cal N}$, that every embedding of
${\cal N}$, that every embedding of 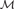 ${\cal M}$ into either degree structure extends to one of
${\cal M}$ into either degree structure extends to one of 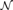 ${\cal N}$ iff
${\cal N}$ iff 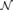 ${\cal N}$ is an end-extension of
${\cal N}$ is an end-extension of 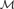 ${\cal M}$.
${\cal M}$.
- Type
- Articles
- Information
- Copyright
- Copyright © The Association for Symbolic Logic 2017


