Hostname: page-component-cd9895bd7-lnqnp Total loading time: 0 Render date: 2024-12-22T20:37:46.311Z Has data issue: false hasContentIssue false
  • English
  • Français

On the angular component map modulo P

Published online by Cambridge University Press:  12 March 2014

Johan Pas
Johan Pas*
Affiliation:
Wiskundig Instituut, Katholieke Universiteit Leuven, 3030 Heverlee, Belgium
Get access Rights & Permissions [Opens in a new window]

Extract

In [10] we introduced a new first order language 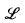for valued fields. This language 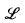has three sorts of variables, namely variables for elements of the valued field, variables for elements of the residue field and variables for elements of the value group. 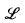contains symbols for the standard field, residue field, and value group operations and a function symbol for the valuation. Essential in our language 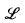is a function symbol for an angular component map modulo P, which is a map from the field to the residue field (see Definition 1.2).

For this language 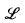we proved a quantifier elimination theorem for Henselian valued fields of equicharacteristic zero which possess such an angular component map modulo P [10, Theorem 4.1]. In the first section of this paper we give some partial results on the existence of an angular component map modulo P on an arbitrary valued field.

By applying the above quantifier elimination theorem to ultraproducts ΠQp/D, we obtained a quantifier elimination, in the language 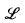, for the p-adic field Qp; and this elimination is uniform for almost all primes p [10, Corollary 4.3]. In §2 we prove that our language 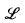is essentially stronger than the natural language for p-adic fields in the sense that the angular component map modulo P cannot be defined, uniformly for almost all p, in terms of the natural language for p-adic fields.

Type
Research Article
Information
The Journal of Symbolic Logic , Volume 55 , Issue 3 , September 1990 , pp. 1125 - 1129
Copyright
Copyright © Association for Symbolic Logic 1990

Access options

Get access to the full version of this content by using one of the access options below. (Log in options will check for institutional or personal access. Content may require purchase if you do not have access.)

References

REFERENCES

[1]Ax, J., A metamathematical approach to some problems in number theory, 1969 number theory institute, Proceedings of Symposia in Pure Mathematics, vol. 20, American Mathematical Society, Providence, Rhode Island, 1971, pp. 161–190.CrossRefGoogle Scholar
[2]Ax, J. and Kochen, S., Diophantine problems over local fields. I, II, III, American Journal of Mathematics, vol. 87 (1965), pp. 605–630, 631–648; Annals of Mathematics, ser. 2, vol. 83 (1966), pp. 437–456.CrossRefGoogle Scholar
[3]Chang, C. C. and Keisler, H. J., Model theory, North-Holland, Amsterdam, 1973.Google Scholar
[4]Cherlin, G., Model-theoretic algebra: selected topics, Lecture Notes in Mathematics, vol. 521, Springer-Verlag, Berlin, 1976.CrossRefGoogle Scholar
[5]Denef, J., p-adic semi-algebraic sets and cell decomposition, Journal für die Reine und Angewandte Mathematik, vol. 369 (1986), pp. 154–166.Google Scholar
[6]Enderton, H. B., A mathematical introduction to logic, Academic Press, New York, 1972.Google Scholar
[7]Fuchs, L., Infinite abelian groups, Academic Press, New York, 1970.Google Scholar
[8]Kochen, S., The model theory of local fields, Logic conference, Kiel 1974, Lecture Notes in Mathematics, vol. 499, Springer-Verlag, Berlin, 1975, pp. 384–425.Google Scholar
[9]Kopperman, R., Model theory audits applications, Allyn and Bacon, Boston, Massachusetts, 1972.Google Scholar
[10]Pas, J., Uniform p-adic cell decomposition and local zeta functions, Journal für die Reine und Angewandte Mathematik, vol. 399 (1989), pp. 137–172.Google Scholar