No CrossRef data available.
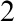 $_2$ SETS
$_2$ SETSPublished online by Cambridge University Press: 13 September 2021
We solve a longstanding question of Soare by showing that if 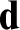 ${\mathbf d}$
is a non-low
${\mathbf d}$
is a non-low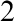 $_2$
computably enumerable degree then
$_2$
computably enumerable degree then 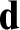 ${\mathbf d}$
contains a c.e. set with no r-maximal c.e. superset.
${\mathbf d}$
contains a c.e. set with no r-maximal c.e. superset.