Hostname: page-component-cd9895bd7-p9bg8 Total loading time: 0 Render date: 2024-12-23T11:31:38.248Z Has data issue: false hasContentIssue false
  • English
  • Français

On sets not belonging to algebras

Published online by Cambridge University Press:  12 March 2014

L. Š. Grinblat
L. Š. Grinblat*
Affiliation:
Department of Mathematics, The College of Judeaand Samaria P.O. Box 3, Ariel 44837, Israel, E-mail: [email protected]
Get access Rights & Permissions [Opens in a new window]

Abstract

Let 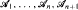be a finite sequence of algebras of sets given on a set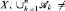 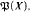with more than 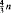pairwise disjoint sets not belonging to 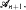It was shown in [4] and [5] that in this case 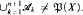Let us consider, instead 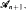a finite sequence of algebras 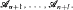It turns out that if for each natural i ≤ l there exist no less than 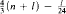pairwise disjoint sets not belonging to 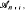then 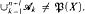But if l ≥ 195 and if for each natural i ≤ l there exist no less than 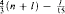pairwise disjoint sets not belonging to 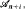then 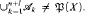After consideration of finite sequences of algebras, it is natural to consider countable sequences of algebras. We obtained two essentially important theorems on a countable sequence of almost σ-algebras (the concept of almost σ-algebra was introduced in [4]).

Keywords

Algebra of setsalmost σ-algebraultrafilterpairwise disjoint sets
Type
Research Article
Information
The Journal of Symbolic Logic , Volume 72 , Issue 2 , June 2007 , pp. 483 - 500
Copyright
Copyright © Association for Symbolic Logic 2007

Access options

Get access to the full version of this content by using one of the access options below. (Log in options will check for institutional or personal access. Content may require purchase if you do not have access.)

References

REFERENCES

[1]Fremlin, D. H., The Gitik-Shelah theorem on real-valued measurable cardinals, Circulated notes, 11 7, 1988.Google Scholar
[2]Fremlin, D. H., Real-valued measurable cardinals, Set theory of the reals (Ramat Gan, 1991), Israel Mathematical Conference Proceedings, vol. 6, 1993, pp. 151–304.Google Scholar
[3]Gitik, M. and Shelah, S., Forcing with ideals and simple forcing notions, Israel Journal of Mathematics, vol. 68 (1989), pp. 129–160.CrossRefGoogle Scholar
[4]Grinblat, L. Š., On sets not belonging to algebras of subsets, Memoirs of the American Mathematical Society, vol. 480(1992).Google Scholar
[5]Grinblat, L. Š., Algebras of sets and combinatorics, Translations of Mathematical Monographs, vol. 214. American Mathematical Society, Providence, RI, 2002.CrossRefGoogle Scholar
[6]Grinblat, L. Š., Theorems on sets not belonging to algebras, Electronic Research Announcements of the American Mathematical Society, vol. 10 (2004), pp. 51–57.CrossRefGoogle Scholar
[7]Kamburelis, A., A new proof of the Gitik–Shelah theorem, Israel Journal of Mathematics, vol. 72 (1990), pp. 373–380.CrossRefGoogle Scholar