Hostname: page-component-586b7cd67f-r5fsc Total loading time: 0 Render date: 2024-11-26T20:25:23.264Z Has data issue: false hasContentIssue false
  • English
  • Français

On regular reduced products*

Published online by Cambridge University Press:  12 March 2014

Juliette Kennedy  and
Saharon Shelah
Juliette Kennedy
Affiliation:
Department of Mathematics, University of Helsinki, Helsinki, Finland, E-mail: [email protected]
Saharon Shelah
Affiliation:
Institute of Mathematics, Hebrew University, Jerusalem, Israel, E-mail: [email protected]
Get access Rights & Permissions [Opens in a new window]

Abstract

Assume (ℵ0, ℵ1) → (λ, λ+). Assume M is a model of a first order theory T of cardinality at most λ+ in a language 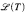of cardinality ≤ λ. Let N be a model with the same language. Let Δ be a set of first order formulas in 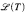and let D be a regular filter on λ. Then M is Δ-embeddable into the reduced power Nλ/D, provided that every Δ-existential formula true in M is true also in N. We obtain the following corollary: for M as above and D a regular ultrafilter over λ, Mλ/D is λ++-universal. Our second result is as follows: For i < μ let Mi, and Ni, be elementarily equivalent models of a language which has cardinality ≤ λ. Suppose D is a regular filter on λ and (ℵ0, ℵ1) → (λ, λ+) holds. We show that then the second player has a winning strategy in the Ehrenfeucht-Fraïssé game of length λ+ on ΠiMi/D and ΠiNi/D. This yields the following corollary: Assume GCH and λ regular (or just (ℵ0, ℵ1) → (λ, λ+) and 2λ = λ+. For L, Mi and Ni be as above, if D is a regular filter on λ, then ΠiMi/D ≅ ΠiNi/D.

Type
Research Article
Information
The Journal of Symbolic Logic , Volume 67 , Issue 3 , September 2002 , pp. 1169 - 1177
Copyright
Copyright © Association for Symbolic Logic 2002

Access options

Get access to the full version of this content by using one of the access options below. (Log in options will check for institutional or personal access. Content may require purchase if you do not have access.)

Footnotes

*

This paper was written while the authors were guests of the Mittag-Leffler Institute, Djursholm, Sweden. The authors are grateful to the Institute for its support.

References

REFERENCES

[1]Benda, M., On reduced products and filters, Ann. Math. Logic, vol. 4 (1972), pp. 1–29.CrossRefGoogle Scholar
[2]Chang, C. C., A note on the two cardinal problem, Proceedings of the American Mathematical Society, vol. 16 (1965), pp. 1148–1155.CrossRefGoogle Scholar
[3]Chang, C.C. and Keisler, J., Model theory, North-Holland.Google Scholar
[4]Hyttinen, T., On κ-complete reduced products, Archive for Mathematical Logic, vol. 31 (1992), no. 3, pp. 193–199.CrossRefGoogle Scholar
[5]Jensen, R., The fine structure of the constructible hierarchy, with a section by Jack Silver, Ann. Math. Logic, vol. 4 (1972), pp. 229–308.CrossRefGoogle Scholar
[6]Jónsson, B. and Olin, P., Almost direct products and saturation, Compositio Mathematica, vol. 20 (1968), pp. 125–132.Google Scholar
[7]Keisler, J., Ultraproducts and saturated models, Koninkttjke Nederlandse Akademie van Weten-schappen. Proceedings. Ser. A 67 (=Indagationes Mathematicae 26), (1964), pp. 178–186.Google Scholar
[8]Kennedy, J. and Shelah, S., On embedding models of arithmetic of cardinality ℵ1 into reduced powers, to appear.Google Scholar
[9]Mitchell, W., Aronszajn trees and the independence of the transfer property, Ann. Math. Logic, vol. 5 (1972/1973), pp. 21–46.CrossRefGoogle Scholar
[10]Shelah, S., For what filters is every reduced product saturated?, Israel Journal of Mathematics, vol. 12 (1972), pp. 23–31.CrossRefGoogle Scholar
[11]Shelah, S., “Gap I” two-cardinal principles and the omitting types theorem for L(Q), Israel Journal of Mathematics, vol. 65 (1989), no. 2, pp. 133–152.CrossRefGoogle Scholar
[12]Shelah, S., Classification theory and the number of non-isomorphic models, second ed., North-Holland Publishing Co., Amsterdam, 1990.Google Scholar