No CrossRef data available.
Published online by Cambridge University Press: 12 March 2014
It is an open problem within the study of recursively enumerable classes of recursively enumerable sets to characterize those recursively enumerable classes which can be recursively enumerated without repetitions. This paper is concerned with a weaker property of r.e. classes, namely that of being recursively enumerable with at most finite repetitions.
This property is shown to behave more naturally: First we prove an extension theorem for classes satisfying this property. Then the analogous theorem for the property of recursively enumerable classes of being recursively enumerable with a bounded number of repetitions is shown not to hold. The index set of the property of recursively enumerable classes “having an enumeration with finite repetitions” is shown to be 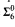 -complete.
-complete.