Hostname: page-component-7479d7b7d-rvbq7 Total loading time: 0 Render date: 2024-07-15T20:22:16.997Z Has data issue: false hasContentIssue false
  • English
  • Français

On projective ordinals1

Published online by Cambridge University Press:  12 March 2014

Alexander S. Kechris
Alexander S. Kechris*
Affiliation:
University of California, Los Angeles, California 90024 Massachusetts Institute of Technology, Cambridge, Massachusetts 02139
Get access Rights & Permissions [Opens in a new window]

Extract

We study in this paper the projective ordinals 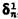, where 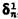= sup{ξ: ξis the length of a Δn1prewellordering of the continuum}. These ordinals were introduced by Moschovakis in [8] to serve as a measure of the “definable length” of the continuum. We prove first in §2 that projective determinacy implies 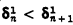, for all even n > 0 (the same result for odd n is due to Moschovakis). Next, in the context of full determinacy, we partly generalize (in §3) the classical fact that δ11 = ℵ1 and the result of Martin that δ31 = ℵω+1 by proving that 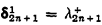, where λ2n+1 is a cardinal of cofinality ω. Finally we discuss in §4 the connection between the projective ordinals and Solovay's uniform indiscernibles. We prove among other things that ∀α(α# exists) implies that every δn1 with n ≥ 3 is a fixed point of the increasing enumeration of the uniform indiscernibles.

Type
Research Article
Information
The Journal of Symbolic Logic , Volume 39 , Issue 2 , June 1974 , pp. 269 - 282
Copyright
Copyright © Association for Symbolic Logic 1974

Access options

Get access to the full version of this content by using one of the access options below. (Log in options will check for institutional or personal access. Content may require purchase if you do not have access.)

Footnotes

1

The results in this paper are included in the author's doctoral dissertation submitted to the University of California, Los Angeles, in June 1972. The author would like to express his sincerest thanks to his thesis advisor, Professor Yiannis N. Moschovakis, both for creating his interest in descriptive set theory and for his guidance and encouragement. The preparation of the paper was partially supported by NSF grant GP-27964.

References

REFERENCES

[1] Addison, J. W. and Moschovakis, Y. N., Some consequences of the axiom of definable determinateness, Proceedings of the National Academy of Sciences, U.S.A., vol. 59 (1968), pp. 708–712.CrossRefGoogle ScholarPubMed
[2] Fenstad, J. E., The axiom of determinateness, Proceedings of the Second Scandinavian Logic Symposium (Fenstad, J. E., Editor), North-Holland, Amsterdam, 1971, pp. 41–61.CrossRefGoogle Scholar
[3] Kechris, A. S. and Moschovakis, Y. N., Two theorems about projective sets, Israel Journal of Mathematics, vol. 12 (1972), pp. 391–399.CrossRefGoogle Scholar
[4] Kechris, A. S. and Moschovakis, Y. N., Notes on the theory of scales, multilithed circulated manuscript.Google Scholar
[5] Kuratowski, K., Topology, vol. 1, Academic Press, New York and London, 1966.Google Scholar
[6] Martin, D. A., The axiom of determinateness and reduction principles in the analytical hierarchy, Bulletin of the American Mathematical Society, vol. 74 (1968), pp. 687–689.CrossRefGoogle Scholar
[7] Martin, D. A., Projective sets and cardinal numbers: some questions related to the continuum problem (to appear).Google Scholar
[8] Moschovakis, Y. N., Determinacy and prewellorderings of the continuum, Mathematical logic and foundations of set theory (Bar-Hillel, Y., Editor), North-Holland, Amsterdam and London, 1970, pp. 24–62.Google Scholar
[9] Moschovakis, Y. N., Uniformization in a playful universe, Bulletin of the American Mathematical Society, vol. 77 (1970), pp. 731–736.CrossRefGoogle Scholar
[10] Mycielski, J., On the axiom of determinateness, Fundamenta Mathematicae, vol. 53 (1964), pp. 205–224.CrossRefGoogle Scholar
[11] Silver, J. H., Some applications of model theory to set theory, Annals of Mathematical Logic, vol. 3 (1971), pp. 45–110.CrossRefGoogle Scholar
[12] Shoenfield, J. R., Mathematical logic, Addison-Wesley, Reading, Massachusetts, 1967.Google Scholar
[13] Solovay, R. M., A nonconstructible Δ3 1 set of integers, Transactions of the American Mathematical Society, vol. 127 (1967), pp. 50–75.Google Scholar