Article contents
On predicates in algebraically closed fields
Published online by Cambridge University Press: 12 March 2014
Extract
Many properties of curves, surfaces, or other varieties in Algebraic Geometry can be formulated in the lower functional calculus as predicates of the coefficients of the polynomial or polynomials which define the variety (curve, surface) in question. For example, the property of a plane curve of order n to possess exactly m double points, or the property to be of genus p — where m and p are specified integers — can be formulated in this way. Similarly many statements on the relation between two or more varieties, e.g., concerning the number and type of their intersection points, can be expressed in the lower functional calculus. It is usual to study the properties of a variety in an algebraically closed field. Accordingly, it is of considerable interest to investigate the general structure of the class of predicates mentioned above in relation to algebraically closed fields. The following result will be proved in the present paper.
Main Theorem. Let F be a commutative algebraic field of arbitrary characteristic, and let F′ = F[x1, …, xn] be the ring of polynomials of n variables with coefficients in F. With every predicate Q{x1, …, xn) which is formulated in the lower functional calculus in terms of the relations of equality, addition, and multiplication and (possibly) in terms of some of the elements of F, there can be associated an ascending chain of ideals in F′,
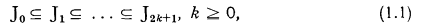
such that
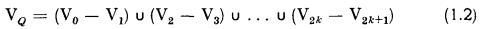
for every extension F* of F which is algebraically closed. In this formula, V0, …, V2k+ 1 are the varieties of the ideals J1, …, J2k+i in the coordinate space Sn: (x1, … xn) over F*, and VQ is the set of points of Sn which satisfy Q.
- Type
- Research Article
- Information
- Copyright
- Copyright © Association for Symbolic Logic 1954
References
REFERENCES
- 5
- Cited by


