Published online by Cambridge University Press: 22 June 2020
In 2004 Atserias, Kolaitis, and Vardi proposed 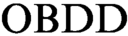 $\text {OBDD}$
-based propositional proof systems that prove unsatisfiability of a CNF formula by deduction of an identically false
$\text {OBDD}$
-based propositional proof systems that prove unsatisfiability of a CNF formula by deduction of an identically false 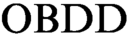 $\text {OBDD}$
from
$\text {OBDD}$
from 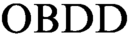 $\text {OBDD}$
s representing clauses of the initial formula. All
$\text {OBDD}$
s representing clauses of the initial formula. All 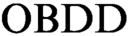 $\text {OBDD}$
s in such proofs have the same order of variables. We initiate the study of
$\text {OBDD}$
s in such proofs have the same order of variables. We initiate the study of 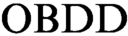 $\text {OBDD}$
based proof systems that additionally contain a rule that allows changing the order in
$\text {OBDD}$
based proof systems that additionally contain a rule that allows changing the order in 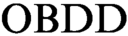 $\text {OBDD}$
s. At first we consider a proof system
$\text {OBDD}$
s. At first we consider a proof system 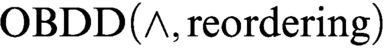 $\text {OBDD}(\land , \text{reordering})$
that uses the conjunction (join) rule and the rule that allows changing the order. We exponentially separate this proof system from
$\text {OBDD}(\land , \text{reordering})$
that uses the conjunction (join) rule and the rule that allows changing the order. We exponentially separate this proof system from 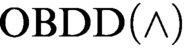 $\text {OBDD}(\land )$
proof system that uses only the conjunction rule. We prove exponential lower bounds on the size of
$\text {OBDD}(\land )$
proof system that uses only the conjunction rule. We prove exponential lower bounds on the size of 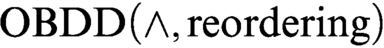 $\text {OBDD}(\land , \text{reordering})$
refutations of Tseitin formulas and the pigeonhole principle. The first lower bound was previously unknown even for
$\text {OBDD}(\land , \text{reordering})$
refutations of Tseitin formulas and the pigeonhole principle. The first lower bound was previously unknown even for 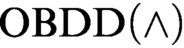 $\text {OBDD}(\land )$
proofs and the second one extends the result of Tveretina et al. from
$\text {OBDD}(\land )$
proofs and the second one extends the result of Tveretina et al. from 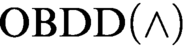 $\text {OBDD}(\land )$
to
$\text {OBDD}(\land )$
to 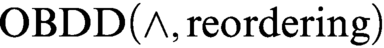 $\text {OBDD}(\land , \text{reordering})$
.
$\text {OBDD}(\land , \text{reordering})$
.
In 2001 Aguirre and Vardi proposed an approach to the propositional satisfiability problem based on 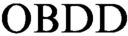 $\text {OBDD}$
s and symbolic quantifier elimination (we denote algorithms based on this approach as
$\text {OBDD}$
s and symbolic quantifier elimination (we denote algorithms based on this approach as 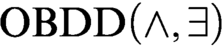 $\text {OBDD}(\land , \exists )$
algorithms). We augment these algorithms with the operation of reordering of variables and call the new scheme
$\text {OBDD}(\land , \exists )$
algorithms). We augment these algorithms with the operation of reordering of variables and call the new scheme 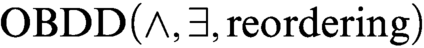 $\text {OBDD}(\land , \exists , \text{reordering})$
algorithms. We notice that there exists an
$\text {OBDD}(\land , \exists , \text{reordering})$
algorithms. We notice that there exists an 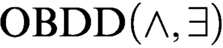 $\text {OBDD}(\land , \exists )$
algorithm that solves satisfiable and unsatisfiable Tseitin formulas in polynomial time (a standard example of a hard system of linear equations over
$\text {OBDD}(\land , \exists )$
algorithm that solves satisfiable and unsatisfiable Tseitin formulas in polynomial time (a standard example of a hard system of linear equations over 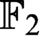 $\mathbb {F}_2$
), but we show that there are formulas representing systems of linear equations over
$\mathbb {F}_2$
), but we show that there are formulas representing systems of linear equations over 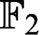 $\mathbb {F}_2$
that are hard for
$\mathbb {F}_2$
that are hard for 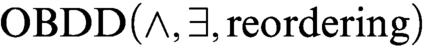 $\text {OBDD}(\land , \exists , \text{reordering})$
algorithms. Our hard instances are satisfiable formulas representing systems of linear equations over
$\text {OBDD}(\land , \exists , \text{reordering})$
algorithms. Our hard instances are satisfiable formulas representing systems of linear equations over 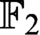 $\mathbb {F}_2$
that correspond to checksum matrices of error correcting codes.
$\mathbb {F}_2$
that correspond to checksum matrices of error correcting codes.
The present paper is an expansion of an earlier conference paper [17]. It includes the contents of [17] augmented with all the proofs that were omitted in the conference version. In addition, the paper contains a new deterministic construction of a hard example for  $\text {OBDD}(\land , \exists )$
algorithms.
$\text {OBDD}(\land , \exists )$
algorithms.