Hostname: page-component-cd9895bd7-hc48f Total loading time: 0 Render date: 2024-12-22T21:04:50.017Z Has data issue: false hasContentIssue false
  • English
  • Français

ON ISOMORPHISM CLASSES OF COMPUTABLY ENUMERABLE EQUIVALENCE RELATIONS

Published online by Cambridge University Press:  13 June 2019

URI ANDREWS  and
SERIKZHAN A. BADAEV
URI ANDREWS
Affiliation:
DEPARTMENT OF MATHEMATICS UNIVERSITY OF WISCONSIN MADISON, WI53706-1388, USA E-mail: [email protected]: http://www.math.wisc.edu/∼andrews/ and
SERIKZHAN A. BADAEV
Affiliation:
DEPARTMENT OF FUNDAMENTAL MATHEMATICS AL-FARABI KAZAKH NATIONAL UNIVERSITY ALMATY050040, KAZAKHSTAN E-mail: [email protected]
Get access Rights & Permissions [Opens in a new window]

Abstract

We examine how degrees of computably enumerable equivalence relations (ceers) under computable reduction break down into isomorphism classes. Two ceers are isomorphic if there is a computable permutation of ω which reduces one to the other. As a method of focusing on nontrivial differences in isomorphism classes, we give special attention to weakly precomplete ceers. For any degree, we consider the number of isomorphism types contained in the degree and the number of isomorphism types of weakly precomplete ceers contained in the degree. We show that the number of isomorphism types must be 1 or ω, and it is 1 if and only if the ceer is self-full and has no computable classes. On the other hand, we show that the number of isomorphism types of weakly precomplete ceers contained in the degree can be any member of 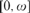$[0,\omega ]$. In fact, for any 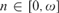$n \in [0,\omega ]$, there is a degree d and weakly precomplete ceers 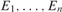${E_1}, \ldots ,{E_n}$ in d so that any ceer R in d is isomorphic to 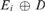${E_i} \oplus D$ for some 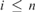$i \le n$ and D a ceer with domain either finite or ω comprised of finitely many computable classes. Thus, up to a trivial equivalence, the degree d splits into exactly n classes.

We conclude by answering some lingering open questions from the literature: Gao and Gerdes [11] define the collection of essentially FC ceers to be those which are reducible to a ceer all of whose classes are finite. They show that the index set of essentially FC ceers is 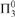${\rm{\Pi }}_3^0$-hard, though the definition is 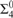${\rm{\Sigma }}_4^0$. We close the gap by showing that the index set is 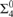${\rm{\Sigma }}_4^0$-complete. They also use index sets to show that there is a ceer all of whose classes are computable, but which is not essentially FC, and they ask for an explicit construction, which we provide.

Andrews and Sorbi [4] examined strong minimal covers of downwards-closed sets of degrees of ceers. We show that if 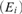$\left( {{E_i}} \right)$ is a uniform c.e. sequence of non universal ceers, then 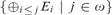$\left\{ {{ \oplus _{i \le j}}{E_i}|j \in \omega } \right\}$ has infinitely many incomparable strong minimal covers, which we use to answer some open questions from [4].

Lastly, we show that there exists an infinite antichain of weakly precomplete ceers.

Keywords

03D25computably enumerable equivalence relationcomputable reducibility on equivalence relationshalting jump
Type
Articles
Information
The Journal of Symbolic Logic , Volume 85 , Issue 1 , March 2020 , pp. 61 - 86
Copyright
Copyright © The Association for Symbolic Logic 2019 

Access options

Get access to the full version of this content by using one of the access options below. (Log in options will check for institutional or personal access. Content may require purchase if you do not have access.)

References

Andrews, U., Badaev, S., and Sorbi, A., A survey on universal computably enumerable equivalence relations. Computability and Complexity: Essays Dedicated to Rodney G. Downey on the Occasion of His 60th Birthday (Day, A., Fellows, M., Greenberg, N., Khoussainov, B., Melnikov, A., and Rosamond, F., editors), Lecture Notes in Computer Science, vol. 10010, Springer, Berlin, 2017, pp. 418–451.CrossRefGoogle Scholar
Andrews, U., Lempp, S., Miller, J. S., Ng, K. M., San Mauro, L., and Sorbi, A., Universal computably enumerable equivalence relations, this Journal, vol. 79 (2014), no. 1, pp. 60–88.Google Scholar
Andrews, U. and Sorbi, A., The complexity of index sets of classes of computably enumerable equivalence relations, this Journal, vol. 81 (2016), no. 4, pp. 1–21.Google Scholar
Andrews, U. and Sorbi, A., Jumps of computably enumerable equivalence relations. Annals of Pure and Applied Logic, vol. 169 (2018), no. 3, pp. 243–259.CrossRefGoogle Scholar
Andrews, U. and Sorbi, A., Joins and meets in the structure of ceers. Computability, vol. 8 (2019), no. 3–4, pp. 193–241.CrossRefGoogle Scholar
Badaev, S. and Sorbi, A., Weakly precomplete computably enumerable equivalence relations. Mathematical Logic Quarterly, vol. 62 (2016), pp. 111–127.CrossRefGoogle Scholar
Ershov, Y. L., Positive equivalences. Algebra and Logic, vol. 10 (1973), no. 6, pp. 378–394.CrossRefGoogle Scholar
Badaev, S. and Sorbi, A., Theory of Numberings, Nauka, Moscow, 1977. (Russian).Google Scholar
Badaev, S. and Sorbi, A., Theory of numberings, Handbook of Computability Theory (Griffor, E. G., editor), Studies in Logic and the Foundations of Mathematics, vol. 140, North-Holland, Amsterdam, 1999, pp. 473–503.Google Scholar
Fokina, E., Khoussainov, B., Semukhin, P., and Turesky, D.. Linear orders realised by c.e. equivalence relations, this Journal, vo. 81 (2016), no. 2, pp. 463–482.Google Scholar
Gao, S. and Gerdes, P., Computably enumerable equivalence realations. Studia Logica, vol. 67 (2001), pp. 27–59.Google Scholar
Gavryushkin, A., Khoussainov, B., and Stephan, F., Reducibilities among equivalence relations induced by recursively enumerable structures. Theoretical Computer Science, vol. 612 (2016), pp. 137–152.CrossRefGoogle Scholar
Gavryushkin, A., Jain, S., Khoussainov, B., and Stephan, F., Graphs realised by r.e. equivalence relations. Annals of Pure and Applied Logic, vol.165 (2014), no. (7–8), pp. 1263–1290.CrossRefGoogle Scholar
Khoussainov, B., A journey to computably enumerable structures (Tutorial Lectures), Sailing Routes in the World of Computation (Manea, F., Miller, R. G., and Nowotka, D., editors), Springer, New York, 2018, pp. 1–19.Google Scholar
Khoussainov, B. and Miasnikov, A., Finitely presented expansions of groups, semigroups, and algebras. Transactions of the American Mathematical Society, vol. 366 (2014), no. 3, pp. 1455–1474.CrossRefGoogle Scholar
Lachlan, A. H., A note on positive equivalence relations. Zeitschrift für Mathematische Logik und Grundlagen der Mathematik, vol. 33 (1987), pp. 43–46.CrossRefGoogle Scholar
Rogers, H. Jr.,Theory of Recursive Functions and Effective Computability, McGraw-Hill, New York, 1967.Google Scholar
Soare, R. I., Recursively Enumerable Sets and Degrees, Perspectives in Mathematical Logic, Omega Series, Springer-Verlag, Heidelberg, 1987.CrossRefGoogle Scholar