Hostname: page-component-6587cd75c8-vfwnz Total loading time: 0 Render date: 2025-04-24T04:59:08.231Z Has data issue: false hasContentIssue false
  • English
  • Français

ON INDESTRUCTIBLE STRONGLY GUESSING MODELS

Part of: Set theory

Published online by Cambridge University Press:  06 January 2025

RAHMAN MOHAMMADPOUR  and
BOBAN VELIČKOVIĆ
RAHMAN MOHAMMADPOUR*
Affiliation:
MATHEMATICAL INSTITUTE OF THE POLISH ACADEMY OF SCIENCES (GDANSK BRANCH) ANTONIEGO ABRAHAMA 18, 81-825, SOPOT POLAND URL: https://sites.google.com/site/rahmanmohammadpour
BOBAN VELIČKOVIĆ
Affiliation:
INSTITUT DE MATHÉMATIQUES DE JUSSIEU - PARIS RIVE GAUCHE UNIVERSITÉ PARIS CITÉ 8 PLACE AURÉLIE NEMOURS 75205 PARIS CEDEX 13 FRANCEE-mail:[email protected] URL: http://www.logique.jussieu.fr/~boban
*
E-mail: [email protected]
Get access Rights & Permissions [Opens in a new window]

Abstract

In [15] we defined and proved the consistency of the principle 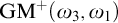$\mathrm {GM}^+(\omega _3,\omega _1)$ which implies that many consequences of strong forcing axioms hold simultaneously at 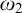$\omega _2$ and 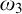$\omega _3$. In this paper we formulate a strengthening of 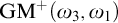$\mathrm {GM}^+(\omega _3,\omega _1)$ that we call 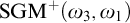$\mathrm {SGM}^+(\omega _3,\omega _1)$. We also prove, modulo the consistency of two supercompact cardinals, that 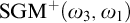$\mathrm {SGM}^+(\omega _3,\omega _1)$ is consistent with ZFC. In addition to all the consequences of 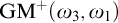$\mathrm {GM}^+(\omega _3,\omega _1)$, the principle 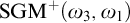$\mathrm {SGM}^+(\omega _3,\omega _1)$, together with some mild cardinal arithmetic assumptions that hold in our model, implies that any forcing that adds a new subset of 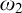$\omega _2$ either adds a real or collapses some cardinal. This gives a partial answer to a question of Abraham [1] and extends a previous result of Todorčević [16] in this direction.

Keywords

guessing modelindestructible guessing modelMagidor modelvirtual modelside conditions

MSC classification

Primary: 03E35: Consistency and independence results 03E55: Large cardinals 03E57: Generic absoluteness and forcing axioms 03E65: Other hypotheses and axioms
Type
Article
Information
The Journal of Symbolic Logic , First View , pp. 1 - 27
Check for updates
Copyright
© The Author(s), 2025. Published by Cambridge University Press on behalf of The Association for Symbolic Logic

Access options

Get access to the full version of this content by using one of the access options below. (Log in options will check for institutional or personal access. Content may require purchase if you do not have access.)

Article purchase

Temporarily unavailable

References

Abraham, U., The isomorphism types of Aronszajn trees and the forcing without the generalized continuum hypothesis , Ph.D. thesis, Hebrew University of Jerusalem, Jerusalem, 1979.Google Scholar
Baumgartner, J., Malitz, J., and Reinhardt, W., Embedding trees in the rationals . Proceedings of the National Academy of Sciences of the United States of America , vol. 67 (1970), pp. 1748–1753.Google Scholar
Baumgartner, J. E., Iterated forcing , Surveys in Set Theory (Mathias, A. R. D., editor), volume 87 of London Mathematical Society Lecture Note Series, Cambridge University Press, Cambridge, 1983, pp. 1–59.Google Scholar
Chodounský, D. and Zapletal, J., Why Y-c.c . Annals of Pure and Applied Logic , vol. 166 (2015), no. 11, pp. 1123–1149,.Google Scholar
Cox, S. and Krueger, J., Quotients of strongly proper forcings and guessing models . The Journal of Symbolic Logic , vol. 81 2016, no. 1, pp. 264–283.Google Scholar
Cox, S. and Krueger, J., Indestructible guessing models and the continuum . Fundamenta Mathematicae , vol. 239 (2017), no. 3, pp. 221–258.Google Scholar
Gilton, T. and Neeman, I., Side conditions and iteration theorems . Appalachian Set Theory , 2016, https://www.math.ucla.edu/~ineeman/scit.pdf/.Google Scholar
Golshani, M. and Shelah, S., Specializing trees and answer to a question of Williams . Journal of Mathematical Logic , vol. 21 (2021), no. 1, Paper No. 2050023, 20.Google Scholar
Hamkins, J. D., Gap forcing . Israel Journal of Mathematics , vol. 125 (2001), no. 1, pp. 237–252.Google Scholar
Krueger, J., Guessing models imply the singular cardinal hypothesis . Proceedings of the American Mathematical Society , vol. 147 (2019), no. 12, pp. 5427–5434.Google Scholar
Laver, R., Certain very large cardinals are not created in small forcing extensions . Annals of Pure and Applied Logic , vol. 149 (2007), no. (1-3), pp. 1–6.Google Scholar
Magidor, M., On the role of supercompact and extendible cardinals in logic . Israel Journal of Mathematics , vol. 10 (1971), no. 2, pp. 147–157,Google Scholar
Mitchell, W. J., Adding closed unbounded subsets of ${\omega}_2$ with finite forcing . Notre Dame Journal of Formal Logic , vol. 46 (2005), no. 3, pp. 357–371, 07.Google Scholar
Mitchell, W. J., $I\left[{\omega}_2\right]$ can be the nonstationary ideal on . Transactions of the American Mathematical Society , vol. 361 (2009), no. 2, pp. 561–601.Google Scholar
Mohammadpour, R. and Velicković, B., Guessing models and the approachability ideal . Journal of Mathematical Logic , vol. 21 (2021), no. 2, Paper No. 2150003, 35.Google Scholar
Todorčević, S., Some combinatorial properties of trees . Bulletin of the London Mathematical Society , vol. 14 (1982), no. 3, pp. 213–217.Google Scholar
Velickovic, B., Iteration of Semiproper Forcing Revisited , 2014, https://arxiv.org/abs/1410.5095.Google Scholar
Viale, M., Guessing models and generalized Laver diamond . Annals of Pure and Applied Logic , vol. 163 (2012), no. 11, pp. 1660–1678.Google Scholar
Viale, M. and Weiß, C., On the consistency strength of the proper forcing axiom . Advances in Mathematics , vol. 228 (2011), no. 5, pp. 2672–2687.Google Scholar
Woodin, W. H., The continuum hypothesis, the generic-multiverse of sets, and the $\varOmega$ conjecture , Set Theory, Arithmetic, and Foundations of Mathematics: Theorems, Philosophies (Kennedy, J. and Kossak, R., editors), volume 36 of Lecture Notes in Logic, Association for Symbolic Logic, La Jolla, 2011, pp. 13–42.Google Scholar