Hostname: page-component-cd9895bd7-fscjk Total loading time: 0 Render date: 2025-01-05T14:34:15.652Z Has data issue: false hasContentIssue false
  • English
  • Français

On homogeneity and definability in the first-order theory of the Turing degrees1

Published online by Cambridge University Press:  12 March 2014

Richard A. Shore
Richard A. Shore*
Affiliation:
Cornell University, Ithaca, New York 14853
Get access Rights & Permissions [Opens in a new window]

Extract

Relativization—the principle that says one can carry over proofs and theorems about partial recursive functions and Turing degrees to functions partial recursive in any given set A and the Turing degrees of sets in which A is recursive—is a pervasive phenomenon in recursion theory. It led H. Rogers, Jr. [15] to ask if, for every degree d, 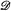(≥ d), the partial ordering of Turing degrees above d, is isomorphic to all the degrees 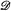. We showed in Shore [17] that this homogeneity conjecture is false. More specifically we proved that if, for some n, the degree of Kleene's 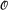(the complete 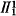set) is recursive in d(n) then 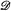≇ 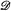(≤ d). The key ingredient of the proof was a new version of a result from Nerode and Shore [13] (hereafter NS I) that any isomorphism φ: 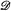→ 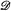(≥ d) must be the identity on some cone, i.e., there is an a called the base of the cone such that b ≥ a ⇒ φ(b) = b. This result was combined with information about minimal covers from Jockusch and Soare [8] and Harrington and Kechris [3] to derive a contradiction from the existence of such an isomorphism if deg(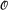) ≤ d(n).

Type
Research Article
Information
The Journal of Symbolic Logic , Volume 47 , Issue 1 , March 1982 , pp. 8 - 16
Copyright
Copyright © Association for Symbolic Logic 1982

Access options

Get access to the full version of this content by using one of the access options below. (Log in options will check for institutional or personal access. Content may require purchase if you do not have access.)

Footnotes

1

Preparation of this paper was partially supported by NSF Grant MCS 77–04013.

References

REFERENCES

[1]Epstein, R., Analysis and degrees ≤ 0′, Notices of the American Mathematical Society, vol. 25 (1978), A–441.Google Scholar
[2]Epstein, R., Degrees of unsohability: Structure and theory, Lecture Notes in Mathematics, vol. 759, Springer-Verlag, Berlin and New York, 1979.Google Scholar
[3]Harrington, L. and Kechris, A., A basis result for Σ30 sets of reals with an application to minimal covers, Proceedings of the American Mathematical Society, vol. 53(1975), pp. 445–448.Google Scholar
[4]Hodes, H., Uniform upper bounds on ideals of Turing degrees, this Journal, vol. 43 (1978), pp. 601–612.Google Scholar
[5]Jockusch, C. G. Jr, Review of Selman [16], Mathematical Reviews, vol. 47 (1974), #3155.Google Scholar
[6]Jockusch, C. G. Jr. and Posner, D., Double jumps of minimal degrees, this Journal, vol. 43 (1978), pp. 715–724.Google Scholar
[7]Jockusch, C. G. Jr. and Simpson, S. G., A degree theoretic definition of the ramified analytical hierarchy, Annals of Mathematical Logic, vol. 10 (1976), pp. 1–32.CrossRefGoogle Scholar
[8]Jockusch, C. G. Jr. and Soare, R. I., Minimal covers and arithmetical sets, Proceedings of the American Mathematical Society, vol. 25 (1970), pp. 856–859.CrossRefGoogle Scholar
[9]Jockusch, C. G. Jr. and Solovay, R. M., Fixed points of jump preserving automorphisms of degrees, Israel Journal of Mathematics, vol. 26 (1977), pp. 91–94.CrossRefGoogle Scholar
[10]Lachlan, A. H. and Lebeuf, R., Countable initial segments of the degrees of unsolvability, this Journal, vol. 41 (1976), pp. 289–300.Google Scholar
[11]Lerman, M., Initial segments of the degrees below 0′, Notices of the American Mathematical Society, vol. 25 (1978), A–506.Google Scholar
[12]Lerman, M., The degrees of unsolvability, Springer-Verlag, Berlin and New York, 1982.Google Scholar
[13]Nerode, A. and Shore, R. A., Second order logic and first order theories of reducibility orderings, Proceedings of the Kleene Symposium (Barwise, J., Keisler, J. and Kunen, K., Editors), North-Holland, Amsterdam, 1979.Google Scholar
[14]Nerode, A. and Shore, R. A., Reducibility orderings: theories, definability and automorphisms, Annals of Mathematical Logic vol. 18 (1980), pp. 61–89.CrossRefGoogle Scholar
[15]Rogers, H. Jr., Theory of recursive functions and effective computability, McGraw-Hill, New York, 1967.Google Scholar
[16]Selman, A. L., Applications of forcing to the degree theory of the arithmetic hierarchy, Proceedings of the London Mathematical Society (3), vol. 25 (1972), pp. 586–602.CrossRefGoogle Scholar
[17]Shore, R. A., The homogeneity conjecture, Proceedings of the National Academy of Sciences USA, vol. 76, no. 9, pp. 4218–4219.CrossRefGoogle Scholar
[18]Simpson, S. G., First order theory of the degrees of recursive unsolvability, Annals of Mathematics (2), vol. 105 (1977), pp. 121–139.CrossRefGoogle Scholar