Published online by Cambridge University Press: 12 March 2014
If one regards an ordinal number as a generalization of a counting number, then it is natural to begin thinking in terms of computations on sets of ordinal numbers. This is precisely what Takeuti [22] had in mind when he initiated the study of recursive functions on ordinals. Kreisel and Sacks [9] too developed an ordinal recursion theory, called metarecursion theory, which specialized to the initial segment of the ordinals bounded by 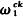 (the first nonconstructive ordinal).
(the first nonconstructive ordinal).
The notion of admissibility was introduced by Kripke [11] and Platek [14] and served to generalize metarecursion theory. Kripke called ordinal α admissible if it satisfied certain closure properties of infinitary computations. It was shown that admissibility could be equivalently formulated in terms of the replacement schema of ZF set theory and that α = 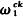 is an admissible ordinal. The study of a recursion theory on an initial segment of the ordinals bounded by some arbitrary admissible α became known as α-recursion theory.
is an admissible ordinal. The study of a recursion theory on an initial segment of the ordinals bounded by some arbitrary admissible α became known as α-recursion theory.
Kripke [10] employed a Gödel numbering scheme to perform an arithmetiza-tion of α -recursion theory and created an analogue to Kleene's T-predicate (cf. [8]) of ordinary recursion theory (o.r.t.). The T-predicate then served as the basis for showing that analogues of the major results of unrelativized o.r.t. held in α-recursion theory; namely, the α-Enumeration Theorem, 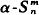 T Theorem, α-Recursion Theorem, and α-Universal Function Theorem.
T Theorem, α-Recursion Theorem, and α-Universal Function Theorem.
The results in this paper appear in the author's Ph.D. dissertation supervised by Martin D. Davis at the Courant Institute, New York University.