Crossref Citations
This article has been cited by the following publications. This list is generated based on data provided by Crossref.
Ebbinghaus, Heinz-Dieter
and
Flum, Jörg
1995.
Finite Model Theory.
p.
307.
Otto, Martin
1997.
Canonization for two variables and puzzles on the square.
Annals of Pure and Applied Logic,
Vol. 85,
Issue. 3,
p.
243.
Hella, Lauri
Kolaitis, Phokion G.
and
Luosto, Kerkko
1997.
How to define a linear order on finite models.
Annals of Pure and Applied Logic,
Vol. 87,
Issue. 3,
p.
241.
Shelah, Saharon
2000.
Computer Science Logic.
Vol. 1862,
Issue. ,
p.
72.
Suppes, P.
2001.
International Encyclopedia of the Social & Behavioral Sciences.
p.
1026.
Niemisto, H.
2005.
On Locality and Uniform Reduction.
p.
41.
Dawar, Anuj
2008.
Logic, Language, Information and Computation.
Vol. 5110,
Issue. ,
p.
17.
Ferreira, Francicleber Martins
and
Martins, Ana Teresa
2009.
Recursive Definitions and Fixed-Points.
Electronic Notes in Theoretical Computer Science,
Vol. 247,
Issue. ,
p.
19.
Dawar, Anuj
Grohe, Martin
Holm, Bjarki
and
Laubner, Bastian
2009.
Logics with Rank Operators.
p.
113.
Grosso, Alejandro L.
and
Turull-Torres, Jose M.
2010.
A Second-Order Logic in Which Variables Range over Relations with Complete First-Order Types.
p.
270.
Ferreira, Francicleber Martins
and
Martins, Ana Teresa
2011.
Recursive definitions and fixed-points on well-founded structures.
Theoretical Computer Science,
Vol. 412,
Issue. 37,
p.
4893.
Grosso, Alejandro L.
and
Torres, José M. Turull
2012.
Conceptual Modelling and Its Theoretical Foundations.
Vol. 7260,
Issue. ,
p.
116.
Hurlbert, Glenn
2013.
Handbook of Graph Theory, Second Edition.
Vol. 20134658,
Issue. ,
p.
1428.
Ferrarotti, Flavio A.
Grosso, Alejandro L.
and
Turull-Torres, José M.
2013.
Semantics in Data and Knowledge Bases.
Vol. 7693,
Issue. ,
p.
174.
Alcón, Liliana
Gutierrez, Marisa
and
Hurlbert, Glenn
2014.
Pebbling in Split Graphs.
SIAM Journal on Discrete Mathematics,
Vol. 28,
Issue. 3,
p.
1449.
Andréka, Hajnal
and
Németi, István
2015.
The Road to Universal Logic.
p.
125.
Suppes, Patrick
2015.
International Encyclopedia of the Social & Behavioral Sciences.
p.
338.
Grädel, Erich
and
Grohe, Martin
2015.
Fields of Logic and Computation II.
Vol. 9300,
Issue. ,
p.
193.
Berkholz, Christoph
and
Nordström, Jakob
2016.
Near-Optimal Lower Bounds on Quantifier Depth and Weisfeiler--Leman Refinement Steps.
p.
267.
Turull-Torres, José Maria
2016.
Foundations of Information and Knowledge Systems.
Vol. 9616,
Issue. ,
p.
311.


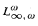 formula with counting quantifiers defines a linear order.
formula with counting quantifiers defines a linear order.