Hostname: page-component-586b7cd67f-gb8f7 Total loading time: 0 Render date: 2024-11-28T22:10:15.658Z Has data issue: false hasContentIssue false
  • English
  • Français

On existence proofs of Hanf numbers1

Published online by Cambridge University Press:  12 March 2014

Harvey Friedman
Harvey Friedman*
Affiliation:
Suny at Buffalo, Amherst, New York 14226
Get access Rights & Permissions [Opens in a new window]

Extract

This paper refines some results of Barwise [1] as well as answering the open question posed at the end of [1] about the Hanf number of 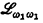positively. We conclude by showing that the existence of a Hanf bound for 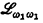cannot be proved in the natural formally intuitionistic set theories with bounded predicates decidable of [3], [4] and [5].

All notation not explained below is taken from [1]. In the Appendix, we give the axioms of ZF0, ZF1, and T in full. We remark that an important point about the axiom of foundation was not emphasized in [1]. This axiom was intended to be the axiom scheme (∀x)((∀y ∈ x)(A(y)) → A(x)) → (∀x)(A(x)), where y does not occur in A = A(x), instead of the more customary (∀x)(∀y)(y ∈ x → (∃z ∈ x)(∀w ∈ z) (w ∉ x)). This is of no consequence in the presence of full separation, but is vital when considering ZF0 and the T below, for with the customary form of foundation, these cannot even prove the existence of Rω+ω .

In [1], a proof of the following is sketched.

Type
Research Article
Information
The Journal of Symbolic Logic , Volume 39 , Issue 2 , June 1974 , pp. 318 - 324
Copyright
Copyright © Association for Symbolic Logic 1974

Access options

Get access to the full version of this content by using one of the access options below. (Log in options will check for institutional or personal access. Content may require purchase if you do not have access.)

Footnotes

1

This research partially supported by NSF grants GP-34091X and GP-038823.

References

REFERENCES

[1] Barwise, J., The Hanf number of second order logic, this Journal, vol. 37 (1972), pp. 588–594.Google Scholar
[2] Friedman, H., Iterated inductive definitions and AC, Proceedings of the 1968 Buffalo Conference on Intuitionism and Proof Theory, North-Holland, Amsterdam, 1969.Google Scholar
[3] Friedman, H., Some applications of Kleen's methods for intuitionistic systems, Proceedings of the 1971 NATO Logic Conference, Springer-Verlag, Berlin and New York, 1973.Google Scholar
[4] Tharp, L., A quasi-intuitionistic set theory, this Journal, vol. 36 (1971), pp. 456–460.Google Scholar
[5] Wolf, R., Formally intuitionistic set theories with bounded predicates decidable, Ph.D Dissertation, Stanford University, 1973.Google Scholar