Hostname: page-component-766f47fc8c-njngn Total loading time: 0 Render date: 2025-03-03T09:24:19.738Z Has data issue: false hasContentIssue false
  • English
  • Français

ON EQUIVALENCE RELATIONS INDUCED BY LOCALLY COMPACT ABELIAN POLISH GROUPS

Part of: Set theory Locally compact abelian groups Abelian groups

Published online by Cambridge University Press:  07 June 2023

LONGYUN DING Open the ORCID record for LONGYUN DING [Opens in a new window]  and
YANG ZHENG
LONGYUN DING
Affiliation:
SCHOOL OF MATHEMATICAL SCIENCES AND LPMC NANKAI UNIVERSITY TIANJIN 300071, P.R. CHINA E-mail: [email protected] E-mail: [email protected]
YANG ZHENG
Affiliation:
SCHOOL OF MATHEMATICAL SCIENCES AND LPMC NANKAI UNIVERSITY TIANJIN 300071, P.R. CHINA E-mail: [email protected] E-mail: [email protected]
Get access Rights & Permissions [Opens in a new window]

Abstract

Given a Polish group G, let 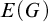$E(G)$ be the right coset equivalence relation $G^{\omega }/c(G)$, where $c(G)$ is the group of all convergent sequences in G. The connected component of the identity of a Polish group G is denoted by 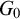$G_0$.

Let 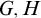$G,H$ be locally compact abelian Polish groups. If $E(G)\leq _B E(H)$, then there is a continuous homomorphism $S:G_0\rightarrow H_0$ such that $\ker (S)$ is non-archimedean. The converse is also true when G is connected and compact.

For 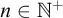$n\in {\mathbb {N}}^+$, the partially ordered set $P(\omega )/\mbox {Fin}$ can be embedded into Borel equivalence relations between $E({\mathbb {R}}^n)$ and $E({\mathbb {T}}^n)$.

Keywords

Borel reductionlocally compact abelian Polish groupequivalence relation

MSC classification

Primary: 03E15: Descriptive set theory
Secondary: 22B05: General properties and structure of LCA groups 20K45: Topological methods
Type
Article
Information
The Journal of Symbolic Logic , First View , pp. 1 - 16
Check for updates
Copyright
© The Author(s), 2023. Published by Cambridge University Press on behalf of The Association for Symbolic Logic

Access options

Get access to the full version of this content by using one of the access options below. (Log in options will check for institutional or personal access. Content may require purchase if you do not have access.)

References

Armacost, D. L., The Structure of Locally Compact Abelian Groups , Monographs and Textbooks in Pure and Applied Mathematics, vol. 68, Marcel Dekker, New York, 1981.Google Scholar
Bella, A., Dow, A., Hart, K. P., Hrusak, M., van Mill, J., and Ursino, P., Embeddings into $P(\mathbb{N})/ \mathit{fin}$ and extension of automorphism . Fundamenta Mathematicae , vol. 174 (2002), pp. 271–284.CrossRefGoogle Scholar
Bondy, J. A. and Murty, U. S. R., Graph Theory , Graduate Texts in Mathematics, vol. 244, Springer-Verlag, Berlin, 2008.CrossRefGoogle Scholar
Ding, L., Borel reducibility and Hölder $\left(\alpha \right)$ embeddability between Banach spaces, this Journal, vol. 77 (2012), pp. 224–244.Google Scholar
Ding, L. and Zheng, Y., On equivalence relations induced by Polish groups, preprint, 2022, arXiv:2204.04594.CrossRefGoogle Scholar
Engelking, R., Dimension Theory , North Holland, New York, 1978.Google Scholar
Gao, S., Invariant Descriptive Set Theory , Monographs and Textbooks in Pure and Applied Mathematics, vol. 293, CRC Press, Boca Raton, FL, 2009.Google Scholar
Gumerov, R. N., On finite-sheeted covering mappings onto solenoids . Proceedings of the American Mathematical Society , vol. 133 (2005), pp. 2771–2778.CrossRefGoogle Scholar
Gutek, A., Solenoids and homeomorphisms on the cantor set . Annales Societatis Mahtematicae Polonae, Series I: Commentationes Mathematicae , vol. XXI (1979), pp. 299–302.Google Scholar
Hewitt, E. and Ross, K. A., Abstract Harmonic Analysis, Volume I: Structure of Topological Groups Integration Theory Group Representations , Springer-Verlag, Berlin, 1963.Google Scholar
Hofmann, K. H. and Morris, S. A., The Structure of Compact Groups , De Gruyter Studies in Mathematics, vol. 25, De Gruyter, Berlin, 2013.CrossRefGoogle Scholar
Kadri, B., Characterization of locally compact groups by closed totally disconnected subgroups . Monatshefte für Mathematik , vol. 199 (2022), pp. 301–313.CrossRefGoogle Scholar
Kechris, A. S., Classical Descriptive Set Theory , Graduate Texts in Mathematics, vol. 156, Springer-Verlag, Berlin, 1995.CrossRefGoogle Scholar
Louveau, A. and Velickovic, B., A note on Borel equivalence relations . Proceedings of the American Mathematical Society , vol. 120 (1994), pp. 255–259.CrossRefGoogle Scholar
Pontrjagin, L., The theory of topological commutative groups . Annals of Mathematics , vol. 35 (1934), pp. 361–388.CrossRefGoogle Scholar
Prajs, J. R., Mutual aposyndesis and products of solenoids . Topology Proceedings , vol. 32 (2008), pp. 339–349.Google Scholar
Scheffer, W., Maps between topological groups that are homotopic to homomorphisms . Proceedings of the American Mathematical Society , vol. 33 (1972), pp. 562–567.CrossRefGoogle Scholar
Yin, Z., Embeddings of $P(\omega )/ \mathsf{Fin}$ into Borel equivalence relations between ${\ell}_p$ and ${\ell}_q$ , this Journal, vol. 80 (2015), pp. 917–939.Google Scholar