Hostname: page-component-78c5997874-94fs2 Total loading time: 0 Render date: 2024-11-16T15:18:13.497Z Has data issue: false hasContentIssue false
  • English
  • Français

On decidable varieties of Heyting algebras

Published online by Cambridge University Press:  12 March 2014

Devdatt P. Dubhashi
Devdatt P. Dubhashi*
Affiliation:
Department of Computer Science, Cornell University, Ithaca, New York 14850, E-mail: [email protected]
Get access Rights & Permissions [Opens in a new window]

Extract

In this paper we present a new proof of a decidability result for the firstorder theories of certain subvarieties of Heyting algebras. By a famous result of Grzegorczyk, the full first-order theory of Heyting algebras is undecidable. In contrast, the first-order theory of Boolean algebras and of many interesting subvarieties of Boolean algebras is decidable by a result of Tarski [8]. In fact, Kozen [6] gives a comprehensive quantitative classification of the complexities of the first-order theories of various subclasses of Boolean algebras (including the full variety).

This stark contrast may be reconciled from the standpoint of universal algebra as arising out of the byplay between structure and decidability: A good structure theory entails positive decidability results. Boolean algebras have a well-developed structure theory [5], while the corresponding theory for Heyting algebras is quite meagre. Viewed in this way, we may hope to obtain decidability results if we focus attention on subclasses of Heyting algebras with good structural properties.

K. Idziak and P. M. Idziak [4] have considered an interesting subvariety of Heyting algebras, 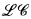, which is the variety generated by all linearly-ordered Heyting algebras. This variety is shown to be the largest subvariety of Heyting algebras with a decidable theory of its finite members. However their proof is rather indirect, proceeding via semantic interpretation into the monadic second order theory of trees. The latter is a powerful theory—it interprets many other theories—but is computationally highly infeasible. In fact, by a celebrated theorem of Rabin, its complexity is not bounded by any elementary recursive function. Consequently, the proof of [4], besides being indirect, also gives no information on the quantitative computational complexity of the theory of .

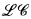Here we pursue the theme of structure and decidability. We isolate the indecomposable algebras in 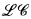and use this to prove a theorem on the structure of if 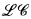-algebras. This theorem relates the 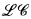-algebras structurally to Boolean algebras. This enables us to bootstrap the known decidability results for Boolean algebras to the variety if .

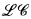Type
Research Article
Information
The Journal of Symbolic Logic , Volume 57 , Issue 3 , September 1992 , pp. 988 - 991
Copyright
Copyright © Association for Symbolic Logic 1992

Access options

Get access to the full version of this content by using one of the access options below. (Log in options will check for institutional or personal access. Content may require purchase if you do not have access.)

References

REFERENCES

[1]Burris, S. and Sankappannavar, H. P., A course in universal algebra, Springer-Verlag, Berlin, 1981.CrossRefGoogle Scholar
[2]Feferman, S. and Vaught, R. L., The first order properties of products of algebraic systems, Fundamenta Mathematicae, vol. 47 (1959), pp. 57–103.CrossRefGoogle Scholar
[3]Ferrante, J. and Rackoff, C. W., The computational complexity of logical theories, Lecture Notes in Mathematics, vol. 718, Springer-Verlag, Berlin, 1979.CrossRefGoogle Scholar
[4]Idziak, K. and Idziak, P. M., Decidability problem for finite Heyting algebras, this Journal, vol. 53 (1988), pp. 729–735.Google Scholar
[5]Koppelberg, S., General theory of Boolean algebras, Handbook of Boolean algebras (Monk, J. D. and Bonnet, R., editors), Vol. I, North-Holland, Amsterdam, 1989.Google Scholar
[6]Kozen, D., Complexity of Boolean algebras, Theoretical Computer Science, vol. 10 (1980), pp. 221–249.CrossRefGoogle Scholar
[7]Rasiowa, H. and Sikorski, R., The mathematics of metamathematics, PWN, Warsaw, 1969.Google Scholar
[8]Tarski, A., Arithmetical classes and types of Boolean algebras, Bulletin of the American Mathematical Society, vol. 55 (1949), pp. 64, 1192 (abstract).Google Scholar