Hostname: page-component-586b7cd67f-dlnhk Total loading time: 0 Render date: 2024-11-28T17:15:22.585Z Has data issue: false hasContentIssue false
  • English
  • Français

On axiomatizing fragments

Published online by Cambridge University Press:  12 March 2014

C. Smorynski
C. Smorynski*
Affiliation:
429 South Warwick Avenue, Westmont, Illinois 60559
Get access Rights & Permissions [Opens in a new window]

Extract

The main purpose of this note is to present new semi-model-theoretic proofs of some axiomatization results. Principally, we prove the result of [van Dalen and Statman] on the axiomatization of the equality fragment of the intuitionistic theory of apartness by ω-fold stability axioms. Further examples are also discussed.

The intuitionistic theories of equality and apartness are given by the following nonlogical axioms:

EQ .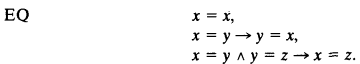

AP .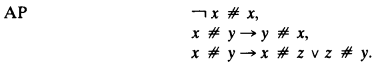

In AP, one can define a notion of equality by means of the abbreviation:

.

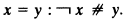The corresponding interpretation of E Q in AP is not faithful — since equality is a negation, we have stability of equality:

.

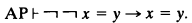The equality fragment of AP is axiomatized by a suitable generalization of the stability of equality. To state it, one first defines a sequence of partial apartness relations:

.

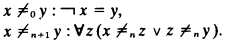A simple induction shows, for all n,

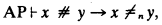
whence

.

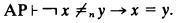Type
Research Article
Information
The Journal of Symbolic Logic , Volume 42 , Issue 4 , December 1977 , pp. 530 - 544
Copyright
Copyright © Association for Symbolic Logic 1977

Access options

Get access to the full version of this content by using one of the access options below. (Log in options will check for institutional or personal access. Content may require purchase if you do not have access.)

References

REFERENCES

van Dalen, D., Lectures on intuitionism, Cambridge Summer School in Mathematical Logic (Mathias, A.R.D. and Rogers, H., Editors), Springer-Verlag, Heidelberg, 1973.Google Scholar
van Dalen, D. and Statman, R., Equality in the presence of apartness (to appear).Google Scholar
Gabbay, D., Semantic proof of Craig's interpolation theorem for intuitionistic logic and extensions. I, II, Logic Colloquium '69 (Gandy, R. and Yates, C.E.M., Editors), North-Holland, Amsterdam, 1971.Google Scholar
Kleene, S.C. and Vesley, R., The foundations of intuitionistic mathematics, North-Holland, Amsterdam, 1965.Google Scholar
Minc, G., Skolem's method of elimination of positive quantifiers in sequential calculi, Doklady Akademii Nauk SSSR, vol. 169 (1966), pp. 861–864.Google Scholar
Osswald, H., Über Skolemerweiterungen in der intuitionistischen Logik mit Gleichheit, Proof Theory Symposium, Kiel 1974 (Diller, J. and Müller, G.H., Editors), Springer-Verlag, Heidelberg, 1975.Google Scholar
Smorynski, C., Applications of Kripke models, Metamathematical investigation of intuitionistic arithmetic and analysis (Troelstra, A.S., Editor), Springer-Verlag, Heidelberg, 1973.Google Scholar