Hostname: page-component-78c5997874-dh8gc Total loading time: 0 Render date: 2024-11-17T10:20:35.014Z Has data issue: false hasContentIssue false
  • English
  • Français

On a question of G. E. Sacks1

Published online by Cambridge University Press:  12 March 2014

Donald A. Martin
Donald A. Martin*
Affiliation:
University of Chicago
Get access Rights & Permissions [Opens in a new window]

Extract

In [1], p. 171, Sacks asks (question (Q5)) whether there is a recursively enumerable degree of unsolvability d such that 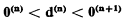for all n ≧ 0. Sacks points out that the set of conditions which d must satisfy is not arithmetical. For this reason he suggests that a proof of (Q5) might require some new combinatorial device. The purpose of this note is to show how (Q5) may be proved simply by extending the methods of [l].2

Type
Research Article
Information
The Journal of Symbolic Logic , Volume 31 , Issue 1 , March 1966 , pp. 66 - 69
Copyright
Copyright © Association for Symbolic Logic 1996

Access options

Get access to the full version of this content by using one of the access options below. (Log in options will check for institutional or personal access. Content may require purchase if you do not have access.)

Footnotes

1

This paper was written while the author was a National Science Foundation Cooperative Fellow.

References

[1]Sacks, G. E., Degrees of unsolvability, Annals of Mathematics Study Number 55, Princeton, 1963.Google Scholar