Hostname: page-component-586b7cd67f-dlnhk Total loading time: 0 Render date: 2024-11-22T22:12:20.573Z Has data issue: false hasContentIssue false
  • English
  • Français

On a conjecture of Dobrinen and Simpson concerning almost everywhere domination

Published online by Cambridge University Press:  12 March 2014

Stephen Binns ,
Bjørn Kjos-Hanssen ,
Manuel Lerman  and
Reed Solomon
Stephen Binns
Affiliation:
Department of Mathematics, University of Connecticut, U-3009, 196 Auditorium Road, Storrs, Ct 06269, USA. E-mail: [email protected]
Bjørn Kjos-Hanssen
Affiliation:
Department of Mathematics, University of Connecticut, U-3009, 196 Auditorium Road, Storrs, Ct 06269, USA. E-mail: [email protected]
Manuel Lerman
Affiliation:
Department of Mathematics, University of Connecticut, U-3009, 196 Auditorium Road, Storrs, Ct 06269, USA. E-mail: [email protected]
Reed Solomon
Affiliation:
Department of Mathematics, University of Connecticut, U-3009, 196 Auditorium Road, Storrs, Ct 06269, USA. E-mail: [email protected]
Get access Rights & Permissions [Opens in a new window]

Extract

Dobrinen and Simpson [4] introduced the notions of almost everywhere domination and uniform almost everywhere domination to study recursion theoretic analogues of results in set theory concerning domination in generic extensions of transitive models of ZFC and to study regularity properties of the Lebesgue measure on 2ω in reverse mathematics. In this article, we examine one of their conjectures concerning these notions.

Throughout this article, ≤T denotes Turing reducibility and μ denotes the Lebesgue (or “fair coin”) probability measure on 2ω given by

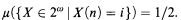
A property holds almost everywhere or for almost all X ∈ 2ω if it holds on a set of measure 1. For f, g ∈ ωω, f dominatesg if ∃m∀n < m(f(n) > g(n)).

(Dobrinen, Simpson). A set A ∈ 2ωis almost everywhere (a.e.) dominating if for almost all X ∈ 2ω and all functions g ≤TX, there is a function f ≤TA such that f dominates g. A is uniformly almost everywhere (u.a.e.) dominating if there is a function f ≤TA such that for almost all X ∈ 2ω and all functions g ≤TX, f dominates g.

There are several trivial but useful observations to make about these definitions. First, although these properties are stated for sets, they are also properties of Turing degrees. That is, a set is (u.)a.e. dominating if and only if every other set of the same degree is (u.)a.e. dominating. Second, both properties are closed upwards in the Turing degrees. Third, u.a.e. domination implies a.e. domination. Finally, if A is u.a.e. dominating, then there is a function f ≤TA which dominates every computable function.

Type
Research Article
Information
The Journal of Symbolic Logic , Volume 71 , Issue 1 , March 2006 , pp. 119 - 136
Copyright
Copyright © Association for Symbolic Logic 2006

Access options

Get access to the full version of this content by using one of the access options below. (Log in options will check for institutional or personal access. Content may require purchase if you do not have access.)

References

REFERENCES

[1]Chaitin, G.J., Algorithmic information theory, Cambridge University Press, Cambridge, 1987.CrossRefGoogle Scholar
[2]Cholak, P., Greenberg, N., and Miller, J.S.. Uniform almost everywhere domination, to appear.Google Scholar
[3]Cholak, P., Jockusch, C.G., and Slaman, T.A., On the strength of Ramsey's Theorem for pairs, this Journal, vol. 66 (2001), pp. 1–55.Google Scholar
[4]Dobrinen, N.L. and Simpson, S.G., Almost everywhere domination, this Journal, vol. 69 (2004), pp. 914–922.Google Scholar
[5]Downey, R. and Hirschfeldt, D.R., Algorithmic randomness and complexity, online manuscript available at www.mcs.vuw.ac.nz/~downey.Google Scholar
[6]Downey, R., Hirschfeldt, D.R., Miller, J., and Nies, A., Relativizing Chaitin's halting probability, submitted.Google Scholar
[7]Jockusch, C.G. Jr. and Soare, R.I., Degrees of members Π10 classes, Pacific Journal of Mathematics, vol. 40 (1972), pp. 605–616.CrossRefGoogle Scholar
[8]Kautz, S., Degrees of random sets, Ph.D. thesis, Cornell University, 1991.Google Scholar
[9]Kučera, A., Measure, Π01-classes and complete extensions of PA, Recursion theory week (Oberwolfach, 1984), Lecture Notes in Mathematics, vol. 1141, Springer, Berlin, 1985, pp. 245–259.CrossRefGoogle Scholar
[10]Kurtz, S., Randomness and genericity in the degrees of unsolvability, Ph.D. thesis. University of Illinois at Urbana-Champaign, 1981.Google Scholar
[11]van Lambalgen, M., Random sequences, Ph.D. thesis, University of Amsterdam, 1987.Google Scholar
[12]Lerman, M., Degrees of unsolvability, Springer, Berlin, 1983.CrossRefGoogle Scholar
[13]Martin, D.A., Classes of recursively enumerable sets and degrees of unsolvability, Zeitschrift für Mathematische Logik und Grundlagen der Mathematik, vol. 12 (1966), pp. 295–310.CrossRefGoogle Scholar
[14]Martin-Löf, P., The definition of random sequences, Information and Control, vol. 9 (1966), pp. 602–619.CrossRefGoogle Scholar
[15]Nies, A., Lowness properties and randomness, Advances in Mathematics, vol. 197 (2005), pp. 274–305.CrossRefGoogle Scholar
[16]Nies, A., Stephan, F., and Terwijn, S., Randomness, relativization and Turing degrees, this Journal, vol. 70 (2005), no. 2, pp. 515–535.Google Scholar
[17]Schwarz, S., Index sets of recursively enumerable sets, quotient lattices, and recursive linear orderings, Ph.D. thesis, University of Chicago, 1982.Google Scholar
[18]Simpson, S.G., Subsystems of second order arithmetic, Springer, Berlin, 1999.CrossRefGoogle Scholar
[19]Soare, R.I., Recursively enumerable sets and degrees, Springer, Berlin, 1987.CrossRefGoogle Scholar
[20]Stillwell, J., Decidability of the “almost all” theory of degrees, this Journal, vol. 37 (1972), pp. 501–506.Google Scholar