Hostname: page-component-586b7cd67f-2plfb Total loading time: 0 Render date: 2024-11-25T22:45:24.786Z Has data issue: false hasContentIssue false
  • English
  • Français

The number of proofs for a BCK-formula

Published online by Cambridge University Press:  12 March 2014

Yuichi Komori  and
Sachio Hirokawa
Yuichi Komori
Affiliation:
Department of Mathematics, Shizuoka University, Shizuoka 422, Japan
Sachio Hirokawa
Affiliation:
Department of Computer Science, College of General Education, Kyushu University, Fukuoka 810, Japan, E-mail: [email protected]
Get access Rights & Permissions [Opens in a new window]

Extract

In this note, we give a necessary and sufficient condition for a BCK-formula to have the unique normal form proof.

We call implicational propositional formulas formulas for short. BCK-formulas are the formulas which are derivable from axioms B = (a → b) → (c → a) → c → b, C = (a→b→c)→b→a→c, and K = a→b→a by substitution and modus ponens. It is known that the property of being a BCK-formula is decidable (Jaskowski [11, Theorem 6.5], Ben-Yelles [3, Chapter 3, Theorem 3.22], Komori [12, Corollary 6]). The set of BCK-formulas is identical to the set of provable formulas in the natural deduction system with the following two inference rules.

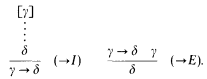
Here γ occurs at most once in (→I). By the formulae-as-types correspondence [10], this set is identical to the set of type-schemes of closed BCK-λ-terms. (See [5].) A BCK-λ-term is a λ-term in which no variable occurs twice. Basic notion concerning the type assignment system can be found [4]. Uniqueness of normal form proofs has been known for balanced formulas. (See [2,14].) It is related to the coherence theorem in cartesian closed categories. A formula is balanced when no variable occurs more than twice in it. It was shown in [8] that the proofs of balanced formulas are BCK-proofs. Relevantly balanced formulas were defined in [9], and it was proved that such formulas have unique normal form proofs. Balanced formulas are included in the set of relevantly balanced formulas.

Type
Research Article
Information
The Journal of Symbolic Logic , Volume 58 , Issue 2 , June 1993 , pp. 626 - 628
Copyright
Copyright © Association for Symbolic Logic 1993

Access options

Get access to the full version of this content by using one of the access options below. (Log in options will check for institutional or personal access. Content may require purchase if you do not have access.)

References

REFERENCES

[1]Akama, Y., The number of proofs and tree automaton. II, manuscript, 10. 1991.Google Scholar
[2]Babaev, A. A. and Soloviev, S. V., A coherence theorem for canonical morphism in cartesian closed categories, Zapiski nauchnykh Seminarov Lenigratlskogo Otdeleniya matematichskogo Instituta imeni V. A. Steklova Akademii Nauk SSSR, vol. 88 (1979), pp. 3–29.Google Scholar
[3]Ben-Yelles, C.-B., Type-assignment in the lambda-calculus, Ph.D. thesis, University College, Swansea, 1979.Google Scholar
[4]Hindley, J. R. and Seldin, J. P., Introduction to Combinators and Lambda-Calculus, Cambridge University Press, London, 1986.Google Scholar
[5]Hindley, J. R., BCK-combinators and linear lambda-terms have types, Theoretical Computer Science, vol. 64 (1989), pp. 97–105.CrossRefGoogle Scholar
[6]Hindley, J. R., BCK and BCI logics, condensed detachment and the 2-property, Notre Dame Journal of Formal Logic, to appear.Google Scholar
[7]Hirokawa, S., Principal types of BCK-lambda terms, Theoretical Computer Science, (to appear).Google Scholar
[8]Hirokawa, S., Balanced formulas, BCK-minimal formulas and their proofs, Proceedings of Symposium on Logical Foundations of Computer Science, (Nerode, and Taitslin, , editors), Lecture Notes in Computer Science, vol. 620, Springer-Verlag, Berlin, and New York, 1992, pp. 198–208.Google Scholar
[9]Hirokawa, S., BCK-formulas having unique proofs, Proceedings of category theory and computer science (Pitt, et al., editors), Lecture Notes in Computer Science, vol. 530, Springer-Verlag, Berlin and New York, 1991, pp. 106–120.CrossRefGoogle Scholar
[10]Howard, W. A., The formulae-as-types notion of construction, To H. B. Curry, Essays on Combinatory Logic, Lambda Calculus and Formalism (Hindley, and Seldin, , editors), Academic Press, Cambridge, Massachusetts, 1980, pp. 479–490.Google Scholar
[11]Jaskowski, S., Uber Tautologien, in welchen keine Variable merh Als zweimal vorkommt, Zeitschrift für Mathematische Logik und Grundlagen der Mathematik, vol. 9 (1963), pp. 219–228.CrossRefGoogle Scholar
[12]Komori, Y., The class of BCC-algebras is not a variety, Mathematica Japonica, vol. 29 (1984), pp. 391–394.Google Scholar
[13]Komori, Y., BCK algebras and lambda calculus, Proceedings of the 10th Symposium on Semigroups, Sakado 1986, Josai University, Sakado, 1987, pp. 5–11.Google Scholar
[14]Mints, G. E., A simple proof of the coherence theorem for cartesian closed categories, manuscript, 1982.Google Scholar