No CrossRef data available.
Published online by Cambridge University Press: 08 February 2018
We show there exists a complete theory in a language of size continuum possessing a unique atomic model which is not constructible. We also show it is consistent with 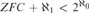 $ZFC + {\aleph _1} < {2^{{\aleph _0}}}$ that there is a complete theory in a language of size
$ZFC + {\aleph _1} < {2^{{\aleph _0}}}$ that there is a complete theory in a language of size 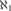 ${\aleph _1}$ possessing a unique atomic model which is not constructible. Finally we show it is consistent with
${\aleph _1}$ possessing a unique atomic model which is not constructible. Finally we show it is consistent with 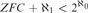 $ZFC + {\aleph _1} < {2^{{\aleph _0}}}$ that for every complete theory T in a language of size
$ZFC + {\aleph _1} < {2^{{\aleph _0}}}$ that for every complete theory T in a language of size 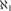 ${\aleph _1}$, if T has uncountable atomic models but no constructible models, then T has
${\aleph _1}$, if T has uncountable atomic models but no constructible models, then T has 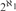 ${2^{{\aleph _1}}}$ atomic models of size
${2^{{\aleph _1}}}$ atomic models of size 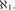 ${\aleph _1}$.
${\aleph _1}$.