Article contents
A note on two-place predicates and fitting sequences of measure functions
Published online by Cambridge University Press: 12 March 2014
Extract
Carnap (in [1], p. 566) has remarked that his measure function m* is fitting for finite languages using a fixed number of one-place predicates, i.e., for any sentence i, m*(i) is the same in all such restricted finite languages in which i occurs. The main purpose of this brief note is to show by means of a counter-example that m* does not have the intuitively desirable property of fittingness when we consider languages using two-place predicates.
We first state for finite languages a general theorem (related to the results in [2]) which guides the construction of large numbers of counter-examples.
Theorem. Let 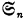 be the symmetric group of n letters. In a language which consists of a finite number of predicates and n individual names, the number of state descriptions in a structure description is equal to the index of some subgroup G in
be the symmetric group of n letters. In a language which consists of a finite number of predicates and n individual names, the number of state descriptions in a structure description is equal to the index of some subgroup G in 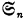 .
.
Proof. Let Σ be a structure description (of a language 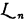 satisfying our hypothesis) and let S be an arbitrary state description in Σ. Let π be a permutation in
satisfying our hypothesis) and let S be an arbitrary state description in Σ. Let π be a permutation in 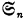 , and let π*S be the state description which results from S by applying the permutation π to the individual names of
, and let π*S be the state description which results from S by applying the permutation π to the individual names of 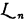 . It is easily verified that for every π in
. It is easily verified that for every π in 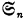 π*S ∊ Σ. Also, for π, ψ in
π*S ∊ Σ. Also, for π, ψ in 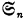 ,
,

We define the set G of permutations as follows :
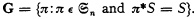 .
.
- Type
- Research Article
- Information
- Copyright
- Copyright © Association for Symbolic Logic 1955
References
REFERENCES
- 1
- Cited by


