Published online by Cambridge University Press: 12 March 2014
The present note is conceived as a sequel to Mostowki's paper, Über die Unabhängigkeit des Wohlordnungssatzes vom Ordnungsprinzip (which will be quoted as “M.”).
In that paper Mostowski considers a system of axioms 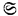 , very close to the system of axiomatic set theory of Bernays, but where the axiom of choice is not supposed to hold. Mostowski proves that the well-ordering theorem (Wohlordnungssatz) cannot be derived from the system
, very close to the system of axiomatic set theory of Bernays, but where the axiom of choice is not supposed to hold. Mostowski proves that the well-ordering theorem (Wohlordnungssatz) cannot be derived from the system 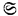 plus the principle of simple ordering (Ordnungsprinzip).
plus the principle of simple ordering (Ordnungsprinzip).
1 Fundamenta mathematicae, vol. 32 (1939), pp. 201–252.
2 Bernays, P., A system of axiomatic set theory, Part I, this Journal, vol. 2 (1937), pp. 65–77Google Scholar, and Part II, ibid., vol. 6 (1941), pp. 1–17.
3 Neumann, J. v., Die Axiomatisierung der Mengenlehre, Mathematische Zeitschrift, vol. 27 (1928), pp. 669–752.Google Scholar
4 In order to avoid conflict with the terminology for one-to-one correspondences, we here translate von Neumann's “Bereich” by “aggregate” rather than by “domain.”
5 See the appropriate definitions below.
6 Cf. Mostowski, A., Über den Begriff einer endlichen Menge, Comptes rendus des séances de la Société des Sciences et des Lettres de Varsovie, Classe III, vol. 31 (1938), pp. 13–20Google Scholar; and A. Lindenbaum and A. Mostowski, Über die Unabhängigkeit des Auswahlaxioms und einiger seiner Folgerungen, ibid., pp. 27–32. The remark is made in the latter paper that the proof may be adapted to various logical and set-theoretic systems—including presumably the system ![]() .
.
7 Tarski, A., Einige Betrachtungen über die Begriffe der ω-Widerspruchsfreiheit und der ω-Vollständigkeit, Monatshefte für Mathematik und Physik, vol. 40 (1933), pp. 97–112.Google Scholar
8 Fraenkel, A., Einleitung in die Mengenlehre, 3rd edn., Berlin 1928.Google Scholar
9 Cf. Tarski, A., Sur les ensembles finis, Fundamenta mathematicae, vol. 6 (1924), pp. 45–95Google Scholar, or J. v. Neumann, loc. cit., Kap. VIII.
10 Cf., e.g., Sierpiński, W., Leçons sur les nombres transfinis, Paris 1928, p. 51.Google Scholar