No CrossRef data available.
Published online by Cambridge University Press: 12 March 2014
In the paper On the logic of quantification Prof. W. V. Quine showed that for the theory of quantification we have a mechanical process to determine whether or not a monadic expression is a valid logical formula, and that to deduce the polyadic theory from the monadic theory we need only the generalized modus ponens, which reads:
If a conditional is valid, and its antecedent consists of zero or more quantifiers followed by a valid schema, then its consequent is valid, i.e.:
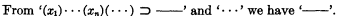
That we have a mechanical process to determine the validity of a monadic expression was pointed out by Löwenheim long ago; Quine's method, however, has the merit that it is very simple and hence practical. The present paper is to show that we may deduce the polyadic theory by means of only a mechanical process and the ordinary modus ponens alone, i.e., the schema,
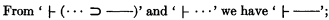
or even by means of only the weakened modus ponens, i.e., the schema,
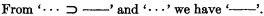
For, if an expression becomes monadic when we omit the initial all-quantifiers (i.e., those preceding every existence-quantifier) and regard the corresponding variables as constants, then evidently we may determine by a mechanical process whether or not it is a valid formula by examining the resulting monadic expression. For example, the expression
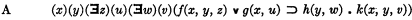
is of the same validity as the expression
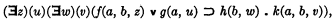
and hence as the expression
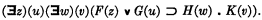
1 Quine, W. V., On the logic of quantification, this Journal, vol. 10 (1945), pp. 1–12 Google Scholar.
2 See, for example, Hilbert, D. and Ackermann, W., Grundzüge der theoretischen Logik, 3rd edn., Springer-Verlag, Berlin-Göttingen-Heidelberg, p. 78 Google Scholar.
3 Berry, G. D. W., On Quine's axioms of quantification, this Journal, vol. 6 (1941), pp. 23–27 Google Scholar.
4 See Quine, W. V., Mathematical logic, Second printing, Harvard University Press, Cambridge, Mass., 1947 Google Scholar. (In the revised edition of 1951, these axioms have the numbers 100, 101, 102, 103. Editor.)