Published online by Cambridge University Press: 12 March 2014
The negative solution of Hilbert's Tenth Problem brought with it a number of unsolvable Diophantine problems. Moreover, by actually providing a Diophantine characterization of recursive enumerability, the proof of the negative solution opened the door to the techniques of recursion theory. In this note, we wish to apply several recursion-theoretic facts and an improvement on the exponential Diophantine representation to refine the exponential case of a result of Davis [1972] regarding the difficulty of determining the number of zeros of a polynomial.
P, Q, etc. will denote polynomials or exponential polynomials–exactly which will be clear from the context. Let # (P) denote the number of distinct nonnegative zeros of P. Further, let C = {0,1, …,ℵ0} be the set of possible values of # (P). For A ⊆ C, we define A * to be
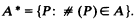
With this notation, Davis' result reads:
Theorem 0.1 (DAVIS). A* is recursive iff A = ∅ or A = C.
The refinement we will prove is:
Theorem 0.2 (Exponential Case). A * is r.e. iff A = ∅ or A = {c: c ≥ a: m} for some finite m.