Hostname: page-component-cd9895bd7-7cvxr Total loading time: 0 Render date: 2024-12-22T20:32:58.400Z Has data issue: false hasContentIssue false
  • English
  • Français

A note on some intermediate propositional calculi

Published online by Cambridge University Press:  12 March 2014

Branislav R. Boričić
Branislav R. Boričić*
Affiliation:
University of Beograd, Kamenička 6, 11000 Beograd, Yugoslavia
Get access Rights & Permissions [Opens in a new window]

Extract

This note is written in reply to López-Escobar's paper [L-E] where a “sequence” of intermediate propositional systems NLCn (n ≥ 1) and corresponding implicative propositional systems NLICn (n ≥ 1) is given. We will show that the “sequence” NLCn contains three different systems only. These are the classical propositional calculus NLC1, Dummett's system NLC2 and the system NLC3. Accordingly (see [C], [Hs2], [Hs3], [B 1], [B2], [Hs4], [L-E]), the problem posed in the paper [L-E] can be formulated as follows: is NLC3a conservative extension of NLIC3? Having in mind investigations of intermediate propositional calculi that give more general results of this type (see V. I. Homič [H1], [H2], C. G. McKay [Mc], T. Hosoi [Hs 1]), in this note, using a result of Homič (Theorem 2, [H1]), we will give a positive solution to this problem.

NLICnand NLCn. If X and Y are propositional logical systems, by X ⊆ Y we mean that the set of all provable formulas of X is included in that of Y. And X = Y means that X ⊆ Y and Y ⊆ X. A(P1/B1, …, Pn/Bn) is the formula (or the sequent) obtained from the formula (or the sequent) A by substituting simultaneously B1, …, Bn for the distinct propositional variables P1, …, Pn in A.

Let Cn(n ≥ 1) be the string of the following sequents:

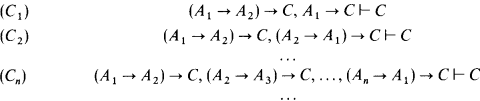
Having in mind that the calculi of sequents can be understood as meta-calculi for the deducibility relation in the corresponding systems of natural deduction (see [P]), the systems of natural deductions NLCn and NLICn (n ≥ 1), introduced in [L-E], can be identified with the calculi of sequents obtained by adding the sequents Cn as axioms to a sequential formulation of the Heyting propositional calculus and to a system of positive implication, respectively (see [C], [Ch], [K], [P]).

Type
Research Article
Information
The Journal of Symbolic Logic , Volume 49 , Issue 2 , June 1984 , pp. 329 - 333
Copyright
Copyright © Association for Symbolic Logic 1984

Access options

Get access to the full version of this content by using one of the access options below. (Log in options will check for institutional or personal access. Content may require purchase if you do not have access.)

References

REFERENCES

[B1]Bull, R. A., The implicational fragment of Dummett's LC, this Journal, vol. 27 (1962), pp. 189–192.Google Scholar
[B2]Bull, R. A., Some results for implicational calculi, this Journal, vol. 29 (1964), pp. 33–39.Google Scholar
[Ch]Church, A., Introduction to mathematical logic. Vol. I, Princeton University Press, Princeton, New Jersey, 1956.Google Scholar
[C]Curry, H. B., Foundations of mathematical logic, McGraw-Hill, New York, 1963.Google Scholar
[D]Dummett, M., A propositional calculus with denumerable matrix, this Journal, vol. 24 (1959), pp. 96–107.Google Scholar
[H1]Homič, V. I., A separability theorem for superinluilionistic propositional calculi, Soviet Mathematics—Doklady, vol. 17 (1976), pp. 1214–1216.Google Scholar
[H2]Homič, V. I., On the problem of separability for superintuitionistic propositional logics, Soviet Mathematics—Doklady, vol. 22 (1980), pp. 476–479.Google Scholar
[Hr]Horn, A., The separation theorem of intuitionist propositional logics, this Journal, vol. 27 (1962), pp. 391–399.Google Scholar
[Hs 1]Hosoi, T., On the separation theorem of intermediate propositional calculi, Proceedings of the Japan Academy, vol. 42 (1966), pp. 535–538.Google Scholar
[Hs2]Hosoi, T., The separation theorem on the classical system, Journal of the Faculty of Science, University of Tokyo, vol. 12 (1966), pp. 223–230.Google Scholar
[Hs 3]Hosoi, T., Algebraic proof of the separation theorem on classical propositional calculus, Proceedings of the Japan Academy, vol. 42 (1966), pp. 67–69.Google Scholar
[Hs4]Hosoi, T., Algebraic proof of the separation theorem on Dummett's LC, Proceedings of the Japan Academy, vol. 42 (1966), pp. 693–695.Google Scholar
[K]Kleene, S. C., Introduction to metamathematics, North-Holland, Amsterdam, 1952.Google Scholar
[L-E]López-Escobar, E. G. K., Implicational logics in natural deduction systems, this Journal, vol. 47 (1982), pp. 184–186.Google Scholar
[Mc]McKay, C. G., The non-separability of a certain finite extension of Heyting's propositional logic, Koninklijke Nederlandse Akademie van Wetenschappen. Proceedings, Series A, vol. 71 (1968), pp. 312–315.Google Scholar
[Pr]Prawitz, D., Natural deduction, Almqvist & Wiksell, Stockholm, 1965.Google Scholar
[W]Wajsberg, M., Untersuchungen über den Aussagenkalkül von A. Heyting, Wiadomości Matematyczne, vol. 46 (1938), pp. 45–101. (See also the Review by B. Rosser in this Journal, vol. 3 (1938), p. 169.)Google Scholar