In this note two independent comments are offered concerning nominalistic syntax.

If one has a nominalistic theory of natural numbers (or positive integers) at one's disposal, one can of course readily formulate a nominalistic syntax by the familiar method of arithmetization. A nominalistic theory of natural numbers is formulated in a previous paper by the author, and thus a basis for a nominalistic syntax is already provided. (The objection that this theory is infinitistic would appear without force, because it provides the only known nominalistic basis for the theory of general recursive functions. On a finitistic basis one merely throws out this vital domain of mathematical theory.)

The second comment is concerned with nominalistic syntax as formulated by Goodman and Quine. The nominalistic construction of natural numbers alluded to above owes much of its power to a primitive device of ancestral quantification. This device is somewhat more powerful than the notions Goodman and Quine allow themselves. Now nominalistic syntax in their somewhat narrower sense can be formulated by utilizing a relation akin to the relation L of the theory of ordered individuals developed elsewhere by the author. ‘L’ here is to designate the relation between inscriptions of being wholly to the left of.

The Goodman-Quine primitive ‘C’, designating a relation of concatenation, and their primitive ‘Part’ with its field confined to inscriptions, can be defined in terms of ‘L’. Thus:

.

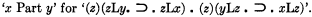(This definition is essentially that of ‘P’ in O.I.)