Consider modal propositional formulae, constructed using proposition-letters, connectives and the modal operators □ and ⋄. The semantic structures are frames, i.e., pairs <W, R> with R ⊆ W2. Let F, V be variables ranging respectively over frames and functions from the set of proposition-letters into the powerset of W. Then the relation

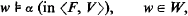
may be defined, for arbitrary formulae α, following the Kripke truth-definition. From this relation we may further define

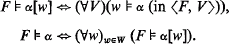
Now, to every modal formula α there corresponds some property Pα of R. A particular example is obtained by considering the well-known translation of modal formulae into formulae of monadic second-order logic with a single binary first-order predicate. For these particular Pα we have

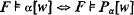
for all F and w ∈ W. These formulae Pα are, however, rather intractable and more convenient ones can often be found. An especially interesting case occurs when Pα may be taken to be some first-order formula. For example, it can be seen that

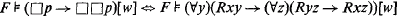
for all F and w ∈ W. It is customary to talk about a related correspondence, namely when for all F we have

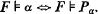
Note that this correspondence holds whenever the first one above holds.