This note arose out of my efforts to understand results of van den Dries, Denef, and Weispfenning on definable Skolem functions in the elementary theory of Qp. The first person to prove their existence was van den Dries, who devised and applied a model-theoretic criterion for theories, admitting elimination of quantifiers, which also admit definable Skolem functions [3]. The proof, though elegant, does not describe how one defines the Skolem functions. In the particular case of Qp, Denef found an ingenious, easily described method for writing out the definitions [2, pp. 14–15]. Unfortunately, his argument directly applies only in the following special case: if

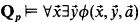
and there is a fixed m ≥ 1 such that

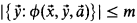
for all 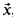, then 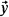can be given as a definable function of 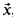. While this special case includes many of interest, van den Dries' theorem seems more general. Weispfenning suggested how his results on primitive-recursive quantifier elimination could produce algorithms yielding definitions of Skolem functions in the specific theories van den Dries considered [10, pp. 470–471]. Though these algorithms provide a more concrete version of van den Dries' theorem, and do not suffer the lack of generality of Denef's result, Weispfenning's argument is extremely subtle and applies only to certain theories of valued fields.