Hostname: page-component-586b7cd67f-l7hp2 Total loading time: 0 Render date: 2024-11-29T09:25:47.309Z Has data issue: false hasContentIssue false
  • English
  • Français

Nonuniformization results for the projective hierarchy

Published online by Cambridge University Press:  12 March 2014

Steve Jackson  and
R. Daniel Mauldin
Steve Jackson
Affiliation:
Department of Mathematics, University of North Texas, Denton, Texas 76203
R. Daniel Mauldin
Affiliation:
Department of Mathematics, University of North Texas, Denton, Texas 76203
Get access Rights & Permissions [Opens in a new window]

Abstract

Let X and Y be uncountable Polish spaces. We show in ZF that there is a coanalytic subset P of X × Y with countable sections which cannot be expressed as the union of countably many partial coanalytic, or even PCA = 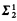, graphs. If X = Y = ωω, P may be taken to be 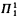. Assuming stronger set theoretic axioms, we identify the least pointclass such that any such coanalytic P can be expressed as the union of countably many graphs in this pointclass. This last result is extended (under suitable hypotheses) to all levels of the projective hierarchy.

Type
Research Article
Information
The Journal of Symbolic Logic , Volume 56 , Issue 2 , June 1991 , pp. 742 - 748
Copyright
Copyright © Association for Symbolic Logic 1991

Access options

Get access to the full version of this content by using one of the access options below. (Log in options will check for institutional or personal access. Content may require purchase if you do not have access.)

References

REFERENCES

[KMS]Kechris, A. S., Martin, D. A. and Solovay, R. M., Introduction to Q-theory, Cabal seminar 79–81, Lecture Notes in Mathematics, vol. 1019, Springer-Verlag, Berlin, 1983, pp. 199–282.CrossRefGoogle Scholar
[Le]Levy, A., Definability in axiomatic set theory, Logic, methodology and philosophy of science (Bar-Hillel, Y., editor), North-Holland, Amsterdam, 1965, pp. 127–151.Google Scholar
[Lu]Lusin, N., Lecons sue les ensembles analytiques et leurs applications, 2nd ed., Chelsea, New York, 1972.Google Scholar
[Ma]Martin, D. A., The largest countable this, that, and the other, Cabal seminar 79–81, Lecture Notes in Mathematics, vol. 1019, Springer-Verlag, Berlin, 1983, pp. 97–106.CrossRefGoogle Scholar
[Mau]Mauldin, R. D., The boundedness of the Cantor-Bendixson order of some analytic sets, Pacific Journal of Mathematics, vol. 74 (1978), pp. 167–177.CrossRefGoogle Scholar
[Mo]Moschovakis, Y. N., Descriptive set theory, North-Holland, Amsterdam, 1980.Google Scholar
[No]Novikov, P. S., Sur les fonctions implicites mesurables B, Fundamenta Mathematicae, vol. 17 (1931), pp. 8–25.CrossRefGoogle Scholar
[W]Woodin, W. H., Private communication, 03 8, 1990.Google Scholar