Published online by Cambridge University Press: 12 March 2014
Let {Wk }k ≥ 0 be a standard enumeration of all recursively enumerable (r.e.) sets. If A is any class of r.e. sets, let θ A denote the index set of A, i.e., θA = {k ∣ Wk ∈ A}. The one-one degrees of index sets form a partial order ℐ which is a proper subordering of the partial order of all one-one degrees. Denote by ⌀ the one-one degree of the empty set, and, if b is the one-one degree of θB, denote by 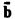 the one-one degree of
the one-one degree of 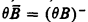 . Let
. Let 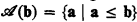 . Let {Ym }m≥0 be the sequence of index sets of nonempty finite classes of finite sets (classified in [5] and independently, in [2]) and denote by a m the one-one degree of Ym . As shown in [2], these degrees are complete at each level of the difference hierarchy generated by the r.e. sets. It was proved in [3] that, for each m ≥ 0,
. Let {Ym }m≥0 be the sequence of index sets of nonempty finite classes of finite sets (classified in [5] and independently, in [2]) and denote by a m the one-one degree of Ym . As shown in [2], these degrees are complete at each level of the difference hierarchy generated by the r.e. sets. It was proved in [3] that, for each m ≥ 0,
(a) a m+1 and ā m+1 are incomparable immediate successors of a m and ā m, and
(b) 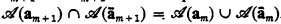 .
.
For m = 0, since Y 0 = θ{⌀}, it follows from (a) that
(c) 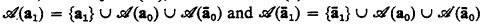 .
.
Hence it follows that
(d) {⌀, 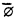 , a o, ā 0, a 1, ā 1 is an initial segment of ℐ.
, a o, ā 0, a 1, ā 1 is an initial segment of ℐ.