Hostname: page-component-6bf8c574d5-7jkgd Total loading time: 0 Render date: 2025-02-17T00:32:24.319Z Has data issue: false hasContentIssue false
  • English
  • Français

Nondiversity in substructures

Published online by Cambridge University Press:  12 March 2014

James H. Schmerl
James H. Schmerl*
Affiliation:
Department of Mathematics, University of Connecticut, Storrs, Connecticut 06269, USA, E-mail: [email protected]
Get access Rights & Permissions [Opens in a new window]

Abstract

For a model 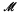of Peano Arithmetic, let Lt(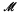) be the lattice of its elementary substructures, and let Lt+ (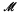) be the equivalenced lattice (Lt(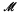),≅),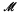 where ≅ 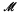is the equivalence relation of isomorphism on Lt(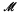). It is known that Lt+(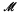) is always a reasonable equivalenced lattice.

Theorem. Let L be a finite distributive lattice and let (L, E) be reasonable. If 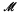0 is a nonstandard prime model of PA, then 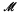0 has a cofinal extension 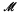such that Lt+(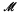) ≅ (L,E).

A general method for proving such theorems is developed which, hopefully, will be able to be applied to some nondistributive lattices.

Type
Research Article
Information
The Journal of Symbolic Logic , Volume 73 , Issue 1 , March 2008 , pp. 193 - 211
Copyright
Copyright © Association for Symbolic Logic 2008

Access options

Get access to the full version of this content by using one of the access options below. (Log in options will check for institutional or personal access. Content may require purchase if you do not have access.)

References

REFERENCES

[1]Abramson, F. G. and Harrington, L. A., Models without indiscernibles, this Journal, vol. 43 (1978), pp. 572–600.Google Scholar
[2]Erdős, P. and Rado, R., A combinatorial theorem, Journal of the London Mathematical Society, vol. 25 (1950), pp. 249–255.CrossRefGoogle Scholar
[3]Erdős, P. and Rado, R., A partition calculus in set theory, Bulletin of the American Mathematical Society, vol. 62 (1956), pp. 427–489.CrossRefGoogle Scholar
[4]Graham, R. L., Rothschild, B., and Spencer, J. H., Ramsey theorey, John Wiley & Sons, New York, 1990.Google Scholar
[5]Hodges, W., Model theory, Encyclopedia of Mathematics and its Applications, vol. 42, Cambridge University Press, Cambridge, 1993.CrossRefGoogle Scholar
[6]Hodges, W., A shorter model theory, Cambridge University Press, Cambridge, 1997.Google Scholar
[7]Kossak, R. and Schmerl, J. H., The structure of models of Peano Arithmetic, Oxford Logic Guides, vol. 50, Oxford University Press, Oxford, 2006.CrossRefGoogle Scholar
[8]Nešetřil, J. and Rödl, V., The Ramsey property for graphs with forbidden complete subgraphs, Journal of Combinatorial Theory, Series B, vol. 20 (1976), pp. 243–249.CrossRefGoogle Scholar
[9]Schmerl, J. H., Substructure lattices of models of Peano Arithmetic, Logic colloquium '84 (Manchester, 1984), North-Holland, Amsterdam, 1986, pp. 225–243.CrossRefGoogle Scholar
[10]Schmerl, J. H., Finite substructure lattices of models of Peano Arithmetic, Proceedings of the American Mathematical Society, vol. 117 (1993), pp. 833–838.CrossRefGoogle Scholar
[11]Schmerl, J. H., Diversity in substructures, Nonstandard models of arithmetic and set theory, Contemporary Mathematics, vol. 361, American Mathematical Society, Providence, 2004, pp. 145–161.CrossRefGoogle Scholar
[12]Voigt, B., Canonizing partition theorems: diversification, products, and iterated versions, Journal of Combinatorial Theory, Series A, vol. 40 (1985), pp. 349–376.CrossRefGoogle Scholar