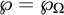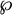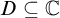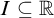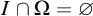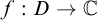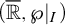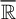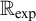1 Introduction
Model theorists have for some time been interested in definability questions concerning structures given by expanding the ordered real field
![]() $\overline {\mathbb {R}}$
by certain functions. For example the sine function is not definable in
$\overline {\mathbb {R}}$
by certain functions. For example the sine function is not definable in
![]() $\mathbb {R}_{\exp }$
, an immediate consequence of the o-minimality of
$\mathbb {R}_{\exp }$
, an immediate consequence of the o-minimality of
![]() $\mathbb {R}_{\exp }$
, which is proved by combining a result of Wilkie in [Reference Wilkie22] and work of Khovanski in [Reference Hovanskiĭ9]. Here and throughout this paper definable means definable with parameters in
$\mathbb {R}_{\exp }$
, which is proved by combining a result of Wilkie in [Reference Wilkie22] and work of Khovanski in [Reference Hovanskiĭ9]. Here and throughout this paper definable means definable with parameters in
![]() $\mathbb {R} $
. In [Reference Bianconi2] Bianconi went further and showed that no non-trivial restriction of sine to a real interval is definable in
$\mathbb {R} $
. In [Reference Bianconi2] Bianconi went further and showed that no non-trivial restriction of sine to a real interval is definable in
![]() $\mathbb {R}_{\exp }$
. This result may be rephrased to say that no restriction of the exponential function to an open disc D in
$\mathbb {R}_{\exp }$
. This result may be rephrased to say that no restriction of the exponential function to an open disc D in
![]() $\mathbb {C}$
is definable in
$\mathbb {C}$
is definable in
![]() $\mathbb {R}_{\exp }$
. Extending this further Bianconi showed in [Reference Bianconi3] that if
$\mathbb {R}_{\exp }$
. Extending this further Bianconi showed in [Reference Bianconi3] that if
![]() $f:D\rightarrow \mathbb {C}$
is holomorphic and definable in
$f:D\rightarrow \mathbb {C}$
is holomorphic and definable in
![]() $\mathbb {R}_{\exp }$
then f is algebraic. In [Reference Peterzil and Starchenko16] Peterzil and Starchenko use this result to characterise all definable locally analytic subsets of
$\mathbb {R}_{\exp }$
then f is algebraic. In [Reference Peterzil and Starchenko16] Peterzil and Starchenko use this result to characterise all definable locally analytic subsets of
![]() $\mathbb {C}^n$
in
$\mathbb {C}^n$
in
![]() $\mathbb {R}_{\exp }$
.
$\mathbb {R}_{\exp }$
.
This question of definability can in fact be generalised to other transcendental functions. Indeed such an example occurs with a transcendental function similar to the exponential function. Consider a complex lattice
![]() $\Omega \subseteq \mathbb {C}$
, a discrete subgroup of rank 2. Associated with each such lattice is the function
$\Omega \subseteq \mathbb {C}$
, a discrete subgroup of rank 2. Associated with each such lattice is the function
 $$ \begin{align*}\wp(z)=\wp_\Omega(z)=\frac{1}{z^2}+\sum_{\substack{\omega\in\Omega\setminus\{0\}}}\left(\frac{1}{(z-\omega)^2}-\frac{1}{\omega^2}\right).\end{align*} $$
$$ \begin{align*}\wp(z)=\wp_\Omega(z)=\frac{1}{z^2}+\sum_{\substack{\omega\in\Omega\setminus\{0\}}}\left(\frac{1}{(z-\omega)^2}-\frac{1}{\omega^2}\right).\end{align*} $$
This function is similar to the exponential function as they are both periodic and have an addition formula as well as a differential equation. Also over the complex field an elliptic curve
![]() $E(\mathbb {C})=E_\Omega (\mathbb {C})\subseteq \mathbb {P}(\mathbb {C})$
is given by the equation
$E(\mathbb {C})=E_\Omega (\mathbb {C})\subseteq \mathbb {P}(\mathbb {C})$
is given by the equation
![]() $Y^2Z=4X^3-g_2XZ^2-g_3Z^3$
, where the complex numbers
$Y^2Z=4X^3-g_2XZ^2-g_3Z^3$
, where the complex numbers
![]() $g_2$
and
$g_2$
and
![]() $g_3$
depend on the lattice
$g_3$
depend on the lattice
![]() $\Omega $
and are known as the invariants of
$\Omega $
and are known as the invariants of
![]() $\wp _\Omega $
. The map
$\wp _\Omega $
. The map
![]() $\exp _E:\mathbb {C}\rightarrow E(\mathbb {C}),z\mapsto [\wp (z):\wp '(z):1]$
is called the exponential map of E. These similarities and the well known model theory of the exponential function make the model theory of the Weierstrass
$\exp _E:\mathbb {C}\rightarrow E(\mathbb {C}),z\mapsto [\wp (z):\wp '(z):1]$
is called the exponential map of E. These similarities and the well known model theory of the exponential function make the model theory of the Weierstrass
![]() $\wp $
-function a natural thing to consider. This has been done by various authors including Bianconi in [Reference Bianconi1], Macintyre in [Reference Macintyre13] as well as Peterzil and Starchenko in [Reference Peterzil and Starchenko15] and Jones, Kirby, and Servi in [Reference Jones, Kirby and Servi10].
$\wp $
-function a natural thing to consider. This has been done by various authors including Bianconi in [Reference Bianconi1], Macintyre in [Reference Macintyre13] as well as Peterzil and Starchenko in [Reference Peterzil and Starchenko15] and Jones, Kirby, and Servi in [Reference Jones, Kirby and Servi10].
During his investigations into the model theory of these Weierstrass
![]() $\wp $
-functions, Macintyre observed the following. If the lattice
$\wp $
-functions, Macintyre observed the following. If the lattice
![]() $\Omega =\mathbb {Z}+i\mathbb {Z}$
then the restriction of
$\Omega =\mathbb {Z}+i\mathbb {Z}$
then the restriction of
![]() $\wp $
to any complex disc D on which
$\wp $
to any complex disc D on which
![]() $\wp $
is analytic is definable in the structure
$\wp $
is analytic is definable in the structure
![]() $(\overline {\mathbb {R}},\wp |_{[1/8,3/8]})$
. The interval
$(\overline {\mathbb {R}},\wp |_{[1/8,3/8]})$
. The interval
![]() $[1/8,3/8]$
is chosen for convenience as it avoids both the poles of
$[1/8,3/8]$
is chosen for convenience as it avoids both the poles of
![]() $\wp $
and the zeros of
$\wp $
and the zeros of
![]() $\wp '$
. Any such interval may be chosen.
$\wp '$
. Any such interval may be chosen.
For the lattice
![]() $\mathbb {Z}+i\mathbb {Z}$
it can immediately be seen that
$\mathbb {Z}+i\mathbb {Z}$
it can immediately be seen that
![]() $\wp (iz)=-\wp (z)$
and this is all that is required to prove Macintyre’s observation. In particular there is a non-integer complex number
$\wp (iz)=-\wp (z)$
and this is all that is required to prove Macintyre’s observation. In particular there is a non-integer complex number
![]() $\alpha $
such that
$\alpha $
such that
![]() $\alpha \Omega \subseteq \Omega $
. A lattice with this property is said to have complex multiplication. A complex lattice
$\alpha \Omega \subseteq \Omega $
. A lattice with this property is said to have complex multiplication. A complex lattice
![]() $\Omega $
is called a real lattice if
$\Omega $
is called a real lattice if
![]() $\overline {\Omega }=\Omega $
. The lattice
$\overline {\Omega }=\Omega $
. The lattice
![]() $\Omega =\mathbb {Z}+i\mathbb {Z}$
is an example of a real lattice which has complex multiplication. In the preprint [Reference McCulloch14] Macintyre’s result is extended to all real lattices with complex multiplication. It is also shown that if the restriction of
$\Omega =\mathbb {Z}+i\mathbb {Z}$
is an example of a real lattice which has complex multiplication. In the preprint [Reference McCulloch14] Macintyre’s result is extended to all real lattices with complex multiplication. It is also shown that if the restriction of
![]() $\wp $
to some open disc
$\wp $
to some open disc
![]() $D\subseteq \mathbb {C}$
is definable in the structure
$D\subseteq \mathbb {C}$
is definable in the structure
![]() $(\overline {\mathbb {R}},\wp |_I)$
, where
$(\overline {\mathbb {R}},\wp |_I)$
, where
![]() $I\subseteq \mathbb {R}$
is a closed interval this does not contain any lattice points and the lattice
$I\subseteq \mathbb {R}$
is a closed interval this does not contain any lattice points and the lattice
![]() $\Omega $
is real, then the lattice
$\Omega $
is real, then the lattice
![]() $\Omega $
has complex multiplication. A direct extension of this result to semiabelian varieties is presumably false. For example consider the semiabelian variety
$\Omega $
has complex multiplication. A direct extension of this result to semiabelian varieties is presumably false. For example consider the semiabelian variety
![]() $G=E\times \mathbb {G}_m$
, where E is an elliptic curve with complex multiplication and
$G=E\times \mathbb {G}_m$
, where E is an elliptic curve with complex multiplication and
![]() $\mathbb {G}_m$
is the multiplicative group. Then a restriction of
$\mathbb {G}_m$
is the multiplicative group. Then a restriction of
![]() $\exp _G$
to the real part of its fundamental domain will give the exponential map
$\exp _G$
to the real part of its fundamental domain will give the exponential map
![]() $\exp _E$
but will not give us, presumably, the full real exponential function.
$\exp _E$
but will not give us, presumably, the full real exponential function.
Now we turn to extending the final aforementioned result of Bianconi to the
![]() $\wp $
-function. The following theorem can be seen as a
$\wp $
-function. The following theorem can be seen as a
![]() $\wp $
-function analogue of Theorem 4 in [Reference Bianconi3].
$\wp $
-function analogue of Theorem 4 in [Reference Bianconi3].
Theorem 1.1. Let
![]() $D\subseteq \mathbb {R}^{2n}$
be a definable open polydisc and
$D\subseteq \mathbb {R}^{2n}$
be a definable open polydisc and
![]() $u,v:D\rightarrow \mathbb {R}$
be two functions that are both definable in the structure
$u,v:D\rightarrow \mathbb {R}$
be two functions that are both definable in the structure
![]() $(\overline {\mathbb {R}},\wp |_I)$
, where
$(\overline {\mathbb {R}},\wp |_I)$
, where
![]() $\Omega $
is a complex lattice which does not have complex multiplication and I is some bounded closed interval in
$\Omega $
is a complex lattice which does not have complex multiplication and I is some bounded closed interval in
![]() $\mathbb {R}$
which does not contain a lattice point. Let
$\mathbb {R}$
which does not contain a lattice point. Let
![]() $f(x,y)=u(x,y)+iv(x,y)$
be holomorphic in D. Then u and v are definable in
$f(x,y)=u(x,y)+iv(x,y)$
be holomorphic in D. Then u and v are definable in
![]() $\overline {\mathbb {R}}$
.
$\overline {\mathbb {R}}$
.
The proof of this theorem is given in Section 4 and adapts the method of Bianconi used to prove Theorem 4 in [Reference Bianconi3]. However the final part of the proof differs from Bianconi’s argument as some of the conclusions are unclear. Bianconi’s method involves using a theorem of Wilkie on smooth functions that are defined implicitly that was proved in general by Jones and Wilkie in [Reference Jones and Wilkie11]. However here we use an implicit definition obtained from a model completeness result due to Gabrielov in [Reference Gabrielov8]. Although the theorem of Gabrielov is well known, as far as we are aware this is the first application of this result in order to obtain an implicit definition of this kind. These implicit definitions are given in Section 3.
In Section 5 we give some nondefinability results for various transcendental functions, beginning with an analogue of the aforementioned result of Peterzil and Starchenko in [Reference Peterzil and Starchenko16] for the Weierstrass
![]() $\wp $
-function. Then we give a characterisation of the definability of restrictions of
$\wp $
-function. Then we give a characterisation of the definability of restrictions of
![]() $\wp $
to a disc
$\wp $
to a disc
![]() $D\subseteq \mathbb {C}$
in terms of the associated lattice
$D\subseteq \mathbb {C}$
in terms of the associated lattice
![]() $\Omega $
having complex multiplication, one direction of which follows from Theorem 1.1. This extends the result in [Reference McCulloch14] to all complex lattices. To complete this section we give a nondefinability result for the modular j-function the proof of which adapts a similar method to the proof of Theorem 1.1. Finally in Section 6 we give some concluding remarks on what other transcendental functions can give rise to similar nondefinability statements and the obstacles that prevent one from proving a version of Theorem 1.1 for such functions using the method of Section 4.
$\Omega $
having complex multiplication, one direction of which follows from Theorem 1.1. This extends the result in [Reference McCulloch14] to all complex lattices. To complete this section we give a nondefinability result for the modular j-function the proof of which adapts a similar method to the proof of Theorem 1.1. Finally in Section 6 we give some concluding remarks on what other transcendental functions can give rise to similar nondefinability statements and the obstacles that prevent one from proving a version of Theorem 1.1 for such functions using the method of Section 4.
2 The Weierstrass
 $\wp $
and modular j functions
$\wp $
and modular j functions
In this section we give background on both the Weierstrass
![]() $\wp $
-function and the modular j-function.
$\wp $
-function and the modular j-function.
Definition 2.1. Let
![]() $\Omega \subseteq \mathbb {C}$
. Then
$\Omega \subseteq \mathbb {C}$
. Then
![]() $\Omega $
is said to be a complex lattice if there exist complex numbers
$\Omega $
is said to be a complex lattice if there exist complex numbers
![]() $\omega _1$
and
$\omega _1$
and
![]() $\omega _2$
such that
$\omega _2$
such that
![]() ${\Omega\hspace{-0.75pt} =\hspace{-0.75pt}\{ m\omega _1\hspace{-0.75pt}+\hspace{-0.75pt}n\omega _2:m,n\hspace{-0.75pt}\in\hspace{-0.75pt} \mathbb {Z},\mathrm {Im\,}(\omega _2/\omega _1)\hspace{-0.75pt}>\hspace{-0.75pt}0 \}}$
. The set
${\Omega\hspace{-0.75pt} =\hspace{-0.75pt}\{ m\omega _1\hspace{-0.75pt}+\hspace{-0.75pt}n\omega _2:m,n\hspace{-0.75pt}\in\hspace{-0.75pt} \mathbb {Z},\mathrm {Im\,}(\omega _2/\omega _1)\hspace{-0.75pt}>\hspace{-0.75pt}0 \}}$
. The set
![]() $\{ \omega _1,\omega _2 \}$
is referred to as an oriented basis for the lattice
$\{ \omega _1,\omega _2 \}$
is referred to as an oriented basis for the lattice
![]() $\Omega $
. The quotient
$\Omega $
. The quotient
![]() $\tau =\omega _2/\omega _1\in \mathbb {H}$
is known as the period ratio of
$\tau =\omega _2/\omega _1\in \mathbb {H}$
is known as the period ratio of
![]() $\Omega $
. The lattice generated by 1 and
$\Omega $
. The lattice generated by 1 and
![]() $\tau $
is denoted
$\tau $
is denoted
![]() $\Omega _{\tau }=\langle 1,\tau \rangle $
.
$\Omega _{\tau }=\langle 1,\tau \rangle $
.
The following theorem can be seen in Chapter 3 in [Reference Chandrasekharan5].
Theorem 2.2. For all
![]() $z\in \mathbb {C}\setminus \Omega $
we have that
$z\in \mathbb {C}\setminus \Omega $
we have that
Therefore the functions
![]() $\wp $
and
$\wp $
and
![]() $\wp '$
are algebraically dependent. Differentiating both sides of this differential equation gives that
$\wp '$
are algebraically dependent. Differentiating both sides of this differential equation gives that
In particular for any
![]() $n\ge 2$
the derivative
$n\ge 2$
the derivative
![]() $\wp ^{(n)}$
may be written as a polynomial with complex coefficients in
$\wp ^{(n)}$
may be written as a polynomial with complex coefficients in
![]() $\wp $
and
$\wp $
and
![]() $\wp '.$
Another crucial property of
$\wp '.$
Another crucial property of
![]() $\wp $
is its addition formula. This can be seen in Theorem 6 of Chapter 3 in [Reference Chandrasekharan5].
$\wp $
is its addition formula. This can be seen in Theorem 6 of Chapter 3 in [Reference Chandrasekharan5].
Theorem 2.3. For complex numbers z and w such that
![]() $z-w\notin \Omega $
we have that
$z-w\notin \Omega $
we have that
 $$ \begin{align} \wp(z+w)=\frac{1}{4}\left(\frac{\wp'(z)-\wp'(w)}{\wp(z)-\wp(w)}\right)^2-\wp(z)-\wp(w). \end{align} $$
$$ \begin{align} \wp(z+w)=\frac{1}{4}\left(\frac{\wp'(z)-\wp'(w)}{\wp(z)-\wp(w)}\right)^2-\wp(z)-\wp(w). \end{align} $$
The function
![]() $\wp '$
also has an addition formula. However this is less well known and may be deduced from the identity
$\wp '$
also has an addition formula. However this is less well known and may be deduced from the identity
 $$ \begin{align} \begin{vmatrix} \wp(z)&\wp'(z)&1\\\wp(w)&\wp'(w)&1\\\wp(z+w)&-\wp'(z+w)&1 \end{vmatrix}=0, \end{align} $$
$$ \begin{align} \begin{vmatrix} \wp(z)&\wp'(z)&1\\\wp(w)&\wp'(w)&1\\\wp(z+w)&-\wp'(z+w)&1 \end{vmatrix}=0, \end{align} $$
which can be seen in page 363 in [Reference Copson6]. The identity (2.4) and consequently the formula (2.3) are also deduced in Sections 20.3 and 20.31 in [Reference Whittaker and Watson21]. From this identity we have for all complex numbers z and w such that
![]() $z-w\notin \Omega $
,
$z-w\notin \Omega $
,
 $$ \begin{align} \wp'(z+w)=\frac{\wp(w)\wp'(z)-\wp'(w)\wp(z)-\wp(z+w)(\wp'(z)-\wp'(w))}{\wp(z)-\wp(w)}. \end{align} $$
$$ \begin{align} \wp'(z+w)=\frac{\wp(w)\wp'(z)-\wp'(w)\wp(z)-\wp(z+w)(\wp'(z)-\wp'(w))}{\wp(z)-\wp(w)}. \end{align} $$
This next definition can be seen in Section 4 of Chapter 1 in [Reference Silverman19].
Definition 2.4. The modular j-function is the function
![]() $j:\mathbb {H}\rightarrow \mathbb {C}$
defined by,
$j:\mathbb {H}\rightarrow \mathbb {C}$
defined by,
 $$ \begin{align*}j(\tau)=1728\frac{g_2^3(\tau)}{g_2^3(\tau)-27g_3^2(\tau)},\end{align*} $$
$$ \begin{align*}j(\tau)=1728\frac{g_2^3(\tau)}{g_2^3(\tau)-27g_3^2(\tau)},\end{align*} $$
where the complex numbers
![]() $g_2$
and
$g_2$
and
![]() $g_3$
are the invariants of the complex lattice
$g_3$
are the invariants of the complex lattice
![]() $\Omega $
with period ratio
$\Omega $
with period ratio
![]() $\tau $
.
$\tau $
.
It turns out that the modular j-function may be written rather differently, namely it has a q-expansion with (positive) integer coefficients. This may be seen in Proposition 7.4 of Chapter 1 in [Reference Silverman19] and the explicit coefficients are in Example 6.2.2 of Chapter 2 in [Reference Silverman19].
Proposition 2.5. Let
![]() $q=e^{2\pi i z}$
. Then,
$q=e^{2\pi i z}$
. Then,
Remark 2.6. From the q-expansion it is clear that the restriction of j to
![]() $\mathbb {H}\cap i\mathbb {R}$
is a real-valued function.
$\mathbb {H}\cap i\mathbb {R}$
is a real-valued function.
By Theorem 4.1 in [Reference Silverman19] the j-function is a modular function of weight zero. That is, for all
![]() $z,w\in \mathbb {C}$
we have that
$z,w\in \mathbb {C}$
we have that
![]() $j(z)=j(w)$
if and only if there is some matrix
$j(z)=j(w)$
if and only if there is some matrix
![]() $\gamma \in SL_2(\mathbb {Z})$
such that
$\gamma \in SL_2(\mathbb {Z})$
such that
 $$ \begin{align*}w=\frac{az+b}{cz+d},\text{ where }\gamma=\begin{pmatrix} a&b\\c&d \end{pmatrix}.\end{align*} $$
$$ \begin{align*}w=\frac{az+b}{cz+d},\text{ where }\gamma=\begin{pmatrix} a&b\\c&d \end{pmatrix}.\end{align*} $$
If
![]() $\gamma $
is a matrix in
$\gamma $
is a matrix in
![]() $GL^+_2(\mathbb {Q})$
, the group of
$GL^+_2(\mathbb {Q})$
, the group of
![]() $2\times 2$
matrices with rational entries and positive determinant, then there is a unique positive integer M such that
$2\times 2$
matrices with rational entries and positive determinant, then there is a unique positive integer M such that
![]() ${M\gamma \in GL_2(\mathbb {Z}})$
and the entries of
${M\gamma \in GL_2(\mathbb {Z}})$
and the entries of
![]() $M\gamma $
are relatively prime. By Proposition 23 in [Reference Zagier23] we have that for each positive integer M there is a polynomial
$M\gamma $
are relatively prime. By Proposition 23 in [Reference Zagier23] we have that for each positive integer M there is a polynomial
![]() $\Phi _M\in \mathbb {Z}[X,Y]$
such that
$\Phi _M\in \mathbb {Z}[X,Y]$
such that
![]() $\Phi _M(j(z),j(w))=0$
if and only if there is a matrix
$\Phi _M(j(z),j(w))=0$
if and only if there is a matrix
![]() $\gamma \in GL^+_2(\mathbb {Q})$
such that
$\gamma \in GL^+_2(\mathbb {Q})$
such that
![]() $z=\gamma w$
and
$z=\gamma w$
and
![]() $\det (M\gamma )=M$
. Finally we note as in [Reference Pila and Tsimerman17] that j satisfies a nonlinear third-order differential equation, namely,
$\det (M\gamma )=M$
. Finally we note as in [Reference Pila and Tsimerman17] that j satisfies a nonlinear third-order differential equation, namely,
 $$ \begin{align} \frac{j"'}{j'}-\frac{3}{2}\left(\frac{j"}{j'}\right)^2+\left(\frac{j^2-1968j+2654208}{2j^2(j-1728)^2}\right)(j')^2=0. \end{align} $$
$$ \begin{align} \frac{j"'}{j'}-\frac{3}{2}\left(\frac{j"}{j'}\right)^2+\left(\frac{j^2-1968j+2654208}{2j^2(j-1728)^2}\right)(j')^2=0. \end{align} $$
To conclude this section we state the versions of the Ax-Schanuel theorem for the Weierstrass
![]() $\wp $
-function and the modular j-function. For the
$\wp $
-function and the modular j-function. For the
![]() $\wp $
-function this is due to Brownawell and Kubota and can be seen in [Reference Brownawell and Kubota4].
$\wp $
-function this is due to Brownawell and Kubota and can be seen in [Reference Brownawell and Kubota4].
Theorem 2.7. Suppose
![]() $\Omega _1,\dots ,\Omega _m$
are complex lattices each of which does not have complex multiplication. Let
$\Omega _1,\dots ,\Omega _m$
are complex lattices each of which does not have complex multiplication. Let
![]() $\tau _1,\dots ,\tau _m$
be their corresponding period ratios and
$\tau _1,\dots ,\tau _m$
be their corresponding period ratios and
![]() $\wp _1,\dots ,\wp _m$
be their corresponding
$\wp _1,\dots ,\wp _m$
be their corresponding
![]() $\wp $
-functions. Suppose that for all
$\wp $
-functions. Suppose that for all
![]() $i,j=1,\dots ,m$
and
$i,j=1,\dots ,m$
and
![]() $i\ne j$
there do not exist integers
$i\ne j$
there do not exist integers
![]() $a,b,c,d$
with
$a,b,c,d$
with
![]() $ad-bc\ne 0$
such that
$ad-bc\ne 0$
such that
Let
![]() $z_1,\dots ,z_n$
be analytic functions on a disc D centred at
$z_1,\dots ,z_n$
be analytic functions on a disc D centred at
![]() $\alpha \in \mathbb {C}$
and suppose that
$\alpha \in \mathbb {C}$
and suppose that
![]() $z_1-z_1(\alpha ),\dots ,z_n-z_n(\alpha )$
are linearly independent over
$z_1-z_1(\alpha ),\dots ,z_n-z_n(\alpha )$
are linearly independent over
![]() $\mathbb {Q}$
. Then we have that
$\mathbb {Q}$
. Then we have that
The version of the Ax-Schanuel theorem for j is due to Pila and Tsimerman in [Reference Pila and Tsimerman17].
Theorem 2.8. Let
![]() $z_1,\dots ,z_n$
be analytic functions defined on a disc
$z_1,\dots ,z_n$
be analytic functions defined on a disc
![]() $D\subseteq \mathbb {C}$
, which take values in the upper half plane, such that
$D\subseteq \mathbb {C}$
, which take values in the upper half plane, such that
![]() $j(z_1),\dots ,j(z_n)$
are non-constant. Suppose that
$j(z_1),\dots ,j(z_n)$
are non-constant. Suppose that
![]() $\Phi _M(j(z_i),j(z_j))\ne 0$
for all positive integers M and for all
$\Phi _M(j(z_i),j(z_j))\ne 0$
for all positive integers M and for all
![]() $i,j=1,\dots ,n$
where
$i,j=1,\dots ,n$
where
![]() $i\ne j$
. Then,
$i\ne j$
. Then,
3 Implicit definitions
The purpose of each of these implicit definitions is to give a low upper bound on the transcendence degree of a finitely generated extension of
![]() $\mathbb {C}$
. Before giving the first of these implicit definitions we give a precise definition of a property used in the statement of these implicit definitions.
$\mathbb {C}$
. Before giving the first of these implicit definitions we give a precise definition of a property used in the statement of these implicit definitions.
Definition 3.1. Let
![]() $\mathcal {F}$
be a countable collection of real analytic functions defined on a bounded interval I in
$\mathcal {F}$
be a countable collection of real analytic functions defined on a bounded interval I in
![]() $\mathbb {R}$
. Let
$\mathbb {R}$
. Let
![]() $f\in \mathcal {F}$
. If the derivatives of f may be written as a polynomial with coefficients in
$f\in \mathcal {F}$
. If the derivatives of f may be written as a polynomial with coefficients in
![]() $\mathbb {C}$
in terms of a finite number of the functions in
$\mathbb {C}$
in terms of a finite number of the functions in
![]() $\mathcal {F}$
then we say that the set
$\mathcal {F}$
then we say that the set
![]() $\mathcal {F}$
is closed under differentiation.
$\mathcal {F}$
is closed under differentiation.
Consider the structure
![]() $(\overline {\mathbb {R}},\mathcal {F})$
with
$(\overline {\mathbb {R}},\mathcal {F})$
with
![]() $\mathcal {F}$
as above. Then if all the derivatives of the functions defined by terms are also defined by terms we say that the structure
$\mathcal {F}$
as above. Then if all the derivatives of the functions defined by terms are also defined by terms we say that the structure
![]() $(\overline {\mathbb {R}},\mathcal {F})$
has a ring of terms that is closed under differentiation.
$(\overline {\mathbb {R}},\mathcal {F})$
has a ring of terms that is closed under differentiation.
3.1 Desingularisation
The first implicit definition comes from ideas of Wilkie in [Reference Wilkie22] and is referred to by Bianconi in [Reference Bianconi2] as the Desingularisation Theorem. A more general form of this implicit definition was proved by Jones and Wilkie in [Reference Jones and Wilkie11]. Let
![]() $\tilde {\mathbb {R}}=(\overline {\mathbb {R}},\mathcal {F})$
be an expansion of
$\tilde {\mathbb {R}}=(\overline {\mathbb {R}},\mathcal {F})$
be an expansion of
![]() $\overline {\mathbb {R}}$
by a set
$\overline {\mathbb {R}}$
by a set
![]() $\mathcal {F}$
of total analytic functions in one variable, closed under differentiation. We also assume that
$\mathcal {F}$
of total analytic functions in one variable, closed under differentiation. We also assume that
![]() $\tilde {\mathbb {R}}$
has a model complete theory and as
$\tilde {\mathbb {R}}$
has a model complete theory and as
![]() $\mathcal {F}$
is closed under differentiation the ring of terms of
$\mathcal {F}$
is closed under differentiation the ring of terms of
![]() $\tilde {\mathbb {R}}$
is closed under differentiation. Before stating the first implicit definition we give a definition.
$\tilde {\mathbb {R}}$
is closed under differentiation. Before stating the first implicit definition we give a definition.
Definition 3.2. Let
![]() $f_1:I\rightarrow \mathbb {R}$
, for some open interval
$f_1:I\rightarrow \mathbb {R}$
, for some open interval
![]() $I\subseteq \mathbb {R}$
, be a function definable in the structure
$I\subseteq \mathbb {R}$
, be a function definable in the structure
![]() $\tilde {\mathbb {R}}=(\overline {\mathbb {R}},\mathcal {F})$
. Then we say that
$\tilde {\mathbb {R}}=(\overline {\mathbb {R}},\mathcal {F})$
. Then we say that
![]() $f_1$
is implicitly
$f_1$
is implicitly
![]() $\mathcal {F}$
-defined if there are some integers
$\mathcal {F}$
-defined if there are some integers
![]() $n,l\ge 1$
, polynomials
$n,l\ge 1$
, polynomials
![]() $P_1,\dots ,P_n$
in
$P_1,\dots ,P_n$
in
![]() $\mathbb {R}[y_1,\dots ,y_{(l+1)(n+1)}]$
and functions
$\mathbb {R}[y_1,\dots ,y_{(l+1)(n+1)}]$
and functions
![]() $f_2,\dots ,f_n:I\rightarrow \mathbb {R}$
such that for all
$f_2,\dots ,f_n:I\rightarrow \mathbb {R}$
such that for all
![]() $z\in I$
,
$z\in I$
,
 $$ \begin{align*}\begin{array}{ccc} F_1(z,f_1(z),\dots,f_n(z))=0,\\\vdots\\F_n(z,f_1(z),\dots,f_n(z))=0, \end{array}\end{align*} $$
$$ \begin{align*}\begin{array}{ccc} F_1(z,f_1(z),\dots,f_n(z))=0,\\\vdots\\F_n(z,f_1(z),\dots,f_n(z))=0, \end{array}\end{align*} $$
and
 $$ \begin{align*}\det\left(\frac{\partial F_i}{\partial x_j}\right)_{\substack{i=1,\dots,n\\j=2,\dots,n+1}}(z,f_1(z),\dots,f_n(z))\ne 0,\end{align*} $$
$$ \begin{align*}\det\left(\frac{\partial F_i}{\partial x_j}\right)_{\substack{i=1,\dots,n\\j=2,\dots,n+1}}(z,f_1(z),\dots,f_n(z))\ne 0,\end{align*} $$
where
 $$ \begin{align*}F_i(z,f_1(z),\dots,f_n(z))=P_i(&z,f_1(z),\dots,f_n(z),\\&g_1(z),g_1(f_1(z)),\dots,g_1(f_n(z)), \dots,\\&g_l(z),g_l(f_1(z)),\dots,g_l(f_n(z)))\end{align*} $$
$$ \begin{align*}F_i(z,f_1(z),\dots,f_n(z))=P_i(&z,f_1(z),\dots,f_n(z),\\&g_1(z),g_1(f_1(z)),\dots,g_1(f_n(z)), \dots,\\&g_l(z),g_l(f_1(z)),\dots,g_l(f_n(z)))\end{align*} $$
for
![]() $g_1,\dots ,g_l\in \mathcal {F}.$
$g_1,\dots ,g_l\in \mathcal {F}.$
Theorem 3.3 (Jones and Wilkie).
Let
![]() $f:I\rightarrow \mathbb {R}$
, for some open interval
$f:I\rightarrow \mathbb {R}$
, for some open interval
![]() $I\subseteq \mathbb {R}$
, be a definable function in
$I\subseteq \mathbb {R}$
, be a definable function in
![]() $\tilde {\mathbb {R}}$
. Then there are subintervals
$\tilde {\mathbb {R}}$
. Then there are subintervals
![]() $I_1,\dots ,I_m\subseteq I$
such that
$I_1,\dots ,I_m\subseteq I$
such that
![]() $I\setminus \left (\cup _{k=1}^m I_k\right )$
is a finite set and f is implicitly
$I\setminus \left (\cup _{k=1}^m I_k\right )$
is a finite set and f is implicitly
![]() $\mathcal {F}$
-defined on each of these subintervals.
$\mathcal {F}$
-defined on each of these subintervals.
3.2 An implicit definition following from a result of Gabrielov
This implicit definition is obtained from a model completeness result of Gabrielov in [Reference Gabrielov8]. As noted in the introduction, although the theorem of Gabrielov is well known, as far as I am aware this is the first application of this theorem in order to obtain an implicit definition of this kind. Firstly we state Gabrielov’s theorem and give some background terminology from [Reference Gabrielov8]. Then we state and prove the implicit definition.
Definition 3.4. Let
![]() $\Phi =\{ \varphi _j\}$
be a set of real analytic functions
$\Phi =\{ \varphi _j\}$
be a set of real analytic functions
![]() $\varphi _j$
defined and analytic on a neighbourhood of the closed unit cube
$\varphi _j$
defined and analytic on a neighbourhood of the closed unit cube
![]() $[0,1]^{n_j}\subseteq \mathbb {R}^{n_j}$
. For every
$[0,1]^{n_j}\subseteq \mathbb {R}^{n_j}$
. For every
![]() $n\ge 0$
, we define
$n\ge 0$
, we define
![]() $A_n=A_n(\Phi )$
as the minimal set of functions with the following properties:
$A_n=A_n(\Phi )$
as the minimal set of functions with the following properties:
-
(1) The constants 0 and 1 and a coordinate function
 $x_1$
on
$x_1$
on
 $\mathbb {R}$
belong to
$\mathbb {R}$
belong to
 $A_1$
.
$A_1$
. -
(2)
 $\varphi _j\in A_{n_j}$
for each j.
$\varphi _j\in A_{n_j}$
for each j. -
(3) If
 $\varphi ,\psi \in A_n$
then
$\varphi ,\psi \in A_n$
then
 $\varphi \pm \psi $
and
$\varphi \pm \psi $
and
 $\varphi \cdot \psi \in A_n$
.
$\varphi \cdot \psi \in A_n$
. -
(4) If
 $\varphi (x_1,\dots ,x_n)\in A_n$
then
$\varphi (x_1,\dots ,x_n)\in A_n$
then
 $\varphi (x_{i(1)},\dots ,x_{i(n)})\in A_{n+m}$
, for any mapping
$\varphi (x_{i(1)},\dots ,x_{i(n)})\in A_{n+m}$
, for any mapping
 $i:\{1,\dots ,n\}\rightarrow \{1,\dots ,n+m\}$
.
$i:\{1,\dots ,n\}\rightarrow \{1,\dots ,n+m\}$
. -
(5) If
 $\varphi (x)\in A_n$
then
$\varphi (x)\in A_n$
then
 $\partial \varphi (x)/\partial x_v\in A_n$
for
$\partial \varphi (x)/\partial x_v\in A_n$
for
 $v=1,\dots ,n$
.
$v=1,\dots ,n$
.
Definition 3.5. A subset
![]() $X\subseteq [0,1]^n$
is called
$X\subseteq [0,1]^n$
is called
![]() $\Phi $
-semianalytic if it is a finite union of sets of the form
$\Phi $
-semianalytic if it is a finite union of sets of the form
where
![]() $f_i,g_j$
are analytic functions from
$f_i,g_j$
are analytic functions from
![]() $A_n(\Phi )$
. A subset
$A_n(\Phi )$
. A subset
![]() $Y\subseteq [0,1]^n$
is called
$Y\subseteq [0,1]^n$
is called
![]() $\Phi $
-subanalytic if it is an image of the projection to
$\Phi $
-subanalytic if it is an image of the projection to
![]() $\mathbb {R}^n$
of a
$\mathbb {R}^n$
of a
![]() $\Phi $
-semianalytic subset
$\Phi $
-semianalytic subset
![]() $X\subseteq [0,1]^{m+n}$
.
$X\subseteq [0,1]^{m+n}$
.
Definition 3.6. For a set
![]() $X\subseteq [0,1]^n,$
let
$X\subseteq [0,1]^n,$
let
![]() $\overline X$
be the closure and
$\overline X$
be the closure and
![]() $\tilde {X}=[0,1]^n\setminus X$
its complement in
$\tilde {X}=[0,1]^n\setminus X$
its complement in
![]() $[0,1]^n$
and
$[0,1]^n$
and
![]() $\partial X=\overline X\setminus X$
its frontier. A semianalytic set
$\partial X=\overline X\setminus X$
its frontier. A semianalytic set
![]() $X\subseteq R^n$
is non-singular of dimension k at a point
$X\subseteq R^n$
is non-singular of dimension k at a point
![]() $x_0\in X$
if there exist real analytic functions
$x_0\in X$
if there exist real analytic functions
![]() $h_1(x),\dots ,h_{n-k}(x)$
defined in an open set U containing
$h_1(x),\dots ,h_{n-k}(x)$
defined in an open set U containing
![]() $x_0$
such that
$x_0$
such that
![]() $dh_1\wedge \dots \wedge dh_{n-k}\ne 0$
at
$dh_1\wedge \dots \wedge dh_{n-k}\ne 0$
at
![]() $x_0$
and
$x_0$
and
![]() $X\cap U=\{ x\in U: h_1(x)=\dots =h_{n-k}(x)=0 \}$
. A semianalytic set is effectively non-singular if the functions
$X\cap U=\{ x\in U: h_1(x)=\dots =h_{n-k}(x)=0 \}$
. A semianalytic set is effectively non-singular if the functions
![]() $h_1,\dots ,h_{n-k}$
can be chosen from the
$h_1,\dots ,h_{n-k}$
can be chosen from the
![]() $f_i$
when X is of the form (3.1). The dimension of a set X is defined as the maximum of its dimensions at non-singular points.
$f_i$
when X is of the form (3.1). The dimension of a set X is defined as the maximum of its dimensions at non-singular points.
Theorem 3.7 (Gabrielov).
Let Y be a
![]() $\Phi $
-subanalytic subset of
$\Phi $
-subanalytic subset of
![]() $[0,1]^n$
. Then
$[0,1]^n$
. Then
![]() $\tilde {Y}=[0,1]^n\setminus Y$
is
$\tilde {Y}=[0,1]^n\setminus Y$
is
![]() $\Phi $
-subanalytic.
$\Phi $
-subanalytic.
Consider a set of restricted real analytic functions
![]() $\Phi $
and a subanalytic set Y defined from the functions in
$\Phi $
and a subanalytic set Y defined from the functions in
![]() $\Phi $
. Then by the previous theorem the complement of Y is defined by functions in the algebra generated by the functions in
$\Phi $
. Then by the previous theorem the complement of Y is defined by functions in the algebra generated by the functions in
![]() $\Phi $
, their partial derivatives, the constants 0 and 1 and the coordinate functions. In particular we have the following corollary.
$\Phi $
, their partial derivatives, the constants 0 and 1 and the coordinate functions. In particular we have the following corollary.
Corollary 3.8 (Gabrielov).
Let
![]() $\mathcal {F}$
be an infinite collection of real analytic functions that are defined on a bounded closed interval in
$\mathcal {F}$
be an infinite collection of real analytic functions that are defined on a bounded closed interval in
![]() $\mathbb {R}$
that is closed under differentiation. Then the structure
$\mathbb {R}$
that is closed under differentiation. Then the structure
![]() $(\overline {\mathbb {R}},\mathcal {F})$
is model complete.
$(\overline {\mathbb {R}},\mathcal {F})$
is model complete.
The following lemma is Lemma 3 in [Reference Gabrielov8] and is required for the proof of the implicit definition.
Lemma 3.9. Let X be a
![]() $\Phi $
-semianalytic set in
$\Phi $
-semianalytic set in
![]() $[0,1]^{m+n}$
, and let
$[0,1]^{m+n}$
, and let
![]() $Y=\pi X\subseteq [0,1]^n,d=\dim Y$
. Then there exist finitely many
$Y=\pi X\subseteq [0,1]^n,d=\dim Y$
. Then there exist finitely many
![]() $\Phi $
-semianalytic subsets
$\Phi $
-semianalytic subsets
![]() $X_v^\prime $
and a
$X_v^\prime $
and a
![]() $\Phi $
-subanalytic subset V of X such that
$\Phi $
-subanalytic subset V of X such that
![]() $Y=\left (\pi V\right )\cup \bigcup _v \pi X_v^\prime $
and
$Y=\left (\pi V\right )\cup \bigcup _v \pi X_v^\prime $
and
![]() $:$
$:$
-
(1)
 $X_v^\prime $
is effectively non-singular,
$X_v^\prime $
is effectively non-singular,
 $\dim X_v^\prime =d$
and
$\dim X_v^\prime =d$
and
 $\pi :X_v^\prime \rightarrow Y$
has rank d at every point of
$\pi :X_v^\prime \rightarrow Y$
has rank d at every point of
 $X_v^\prime $
for each v.
$X_v^\prime $
for each v. -
(2)
 $\dim \pi V<d.$
$\dim \pi V<d.$
-
(3)
 $X_u^\prime \cap X_v^\prime =\varnothing ,$
for
$X_u^\prime \cap X_v^\prime =\varnothing ,$
for
 $u\ne v$
.
$u\ne v$
.
Now we shall state and prove the implicit definition that arises from Gabrielov’s theorem.
Proposition 3.10. Let
![]() $\mathcal {F}$
be a set of real analytic functions defined on a neighbourhood in
$\mathcal {F}$
be a set of real analytic functions defined on a neighbourhood in
![]() $[0,1]$
that contains a closed interval I, suppose that
$[0,1]$
that contains a closed interval I, suppose that
![]() $\mathcal {F}$
is closed under differentiation and consider the structure
$\mathcal {F}$
is closed under differentiation and consider the structure
![]() $(\overline {\mathbb {R}},\mathcal {F}|_I)$
, where
$(\overline {\mathbb {R}},\mathcal {F}|_I)$
, where ![]() . Let
. Let
![]() $f:U\rightarrow I^k$
where
$f:U\rightarrow I^k$
where
![]() $U\subseteq I^m$
for some
$U\subseteq I^m$
for some
![]() $m,k\ge 1$
be a function definable in
$m,k\ge 1$
be a function definable in
![]() $(\overline {\mathbb {R}},\mathcal {F})$
and let
$(\overline {\mathbb {R}},\mathcal {F})$
and let
![]() $f_1,\dots ,f_k:U\rightarrow I$
denote its coordinate functions.
$f_1,\dots ,f_k:U\rightarrow I$
denote its coordinate functions.
Then there exist integers
![]() $n,l \ge 1$
, polynomials
$n,l \ge 1$
, polynomials
![]() $P_1,\dots ,P_n$
in
$P_1,\dots ,P_n$
in
![]() $\mathbb {R}[y_1,\dots ,y_{(l+1)(m+n)}]$
, functions
$\mathbb {R}[y_1,\dots ,y_{(l+1)(m+n)}]$
, functions
![]() $f_{k+1},\dots ,f_n:B\rightarrow I$
for an open box
$f_{k+1},\dots ,f_n:B\rightarrow I$
for an open box
![]() $B\subseteq U$
and
$B\subseteq U$
and
![]() $g_1,\dots ,g_l\in \mathcal {F}$
such that for all
$g_1,\dots ,g_l\in \mathcal {F}$
such that for all
![]() $\bar {z}=(z_1,\dots ,z_m)\in B$
,
$\bar {z}=(z_1,\dots ,z_m)\in B$
,
 $$ \begin{align*}\begin{array}{ccc} F_1(\bar{z},f_1(\bar{z}),\dots,f_n(\bar{z}))=0,\\\vdots\\F_{n}(\bar{z},f_1(\bar{z}),\dots,f_n(\bar{z}))=0, \end{array}\end{align*} $$
$$ \begin{align*}\begin{array}{ccc} F_1(\bar{z},f_1(\bar{z}),\dots,f_n(\bar{z}))=0,\\\vdots\\F_{n}(\bar{z},f_1(\bar{z}),\dots,f_n(\bar{z}))=0, \end{array}\end{align*} $$
and
 $$ \begin{align*}\det\left(\frac{\partial F_i}{\partial x_j}\right)_{\substack{i=1,\dots,n\\j=m+1,\dots,m+n}}(\bar{z},f_1(\bar{z}),\dots,f_n(\bar{z}))\ne0,\end{align*} $$
$$ \begin{align*}\det\left(\frac{\partial F_i}{\partial x_j}\right)_{\substack{i=1,\dots,n\\j=m+1,\dots,m+n}}(\bar{z},f_1(\bar{z}),\dots,f_n(\bar{z}))\ne0,\end{align*} $$
where
 $$ \begin{align*}F_i(\bar{z},f_1(\bar{z}),\dots,f_n(\bar{z}))=P_i(&\bar{z},f_1(\bar{z}),\dots,f_n(\bar{z}),\\&g_1(z_1),\dots,g_1(z_m),g_1(f_1(\bar{z})),\dots,g_1(f_n(\bar{z})), \dots,\\& g_l(z_1),\dots,g_l(z_m),g_l(f_1(\bar{z})),\dots,g_l(f_n(\bar{z}))). \end{align*} $$
$$ \begin{align*}F_i(\bar{z},f_1(\bar{z}),\dots,f_n(\bar{z}))=P_i(&\bar{z},f_1(\bar{z}),\dots,f_n(\bar{z}),\\&g_1(z_1),\dots,g_1(z_m),g_1(f_1(\bar{z})),\dots,g_1(f_n(\bar{z})), \dots,\\& g_l(z_1),\dots,g_l(z_m),g_l(f_1(\bar{z})),\dots,g_l(f_n(\bar{z}))). \end{align*} $$
Proof Here the functions in
![]() $\mathcal {F}$
are defined on a neighbourhood in
$\mathcal {F}$
are defined on a neighbourhood in
![]() $[0,1]$
rather than a neighbourhood containing
$[0,1]$
rather than a neighbourhood containing
![]() $[0,1]$
. This has a slight impact on the definitions and results of Gabrielov that we wish to apply, namely that the interval
$[0,1]$
. This has a slight impact on the definitions and results of Gabrielov that we wish to apply, namely that the interval
![]() $I\subseteq [0,1]$
takes the place of
$I\subseteq [0,1]$
takes the place of
![]() $[0,1]$
in the above statements. Let
$[0,1]$
in the above statements. Let
![]() $Y=\Gamma (f)\subseteq \mathbb {R}^{m+1}$
be the graph of f. Clearly
$Y=\Gamma (f)\subseteq \mathbb {R}^{m+1}$
be the graph of f. Clearly
![]() $\dim Y=m$
. Then Y is a definable set in the structure
$\dim Y=m$
. Then Y is a definable set in the structure
![]() $(\overline {\mathbb {R}},\mathcal {F})$
and by Corollary 3.8 the set Y is a
$(\overline {\mathbb {R}},\mathcal {F})$
and by Corollary 3.8 the set Y is a
![]() $\mathcal {F}$
-subanalytic set of dimension m. By definition
$\mathcal {F}$
-subanalytic set of dimension m. By definition
![]() $Y=\pi X$
where X is a
$Y=\pi X$
where X is a
![]() $\mathcal {F}$
-semianalytic subset of
$\mathcal {F}$
-semianalytic subset of
![]() $\mathbb {R}^{m+n}$
for some n. By Lemma 3.9 we have that
$\mathbb {R}^{m+n}$
for some n. By Lemma 3.9 we have that
![]() $Y=\left (\pi V\right )\cup \bigcup \pi X_v'$
where
$Y=\left (\pi V\right )\cup \bigcup \pi X_v'$
where
![]() $X_v'$
are effectively non-singular
$X_v'$
are effectively non-singular
![]() $\mathcal {F}$
-semianalytic sets of dimension m and
$\mathcal {F}$
-semianalytic sets of dimension m and
![]() $\pi V$
is small. It is enough to prove the result for
$\pi V$
is small. It is enough to prove the result for
![]() $Y=\pi X_v'$
for a single effectively non-singular set
$Y=\pi X_v'$
for a single effectively non-singular set
![]() $X_v'$
. By the definition of an effectively non-singular set and the rank condition seen in Definition 3 in [Reference Gabrielov8] the function f may be defined by a non-singular system of
$X_v'$
. By the definition of an effectively non-singular set and the rank condition seen in Definition 3 in [Reference Gabrielov8] the function f may be defined by a non-singular system of
![]() $m+n-m$
equations as described in the statement.
$m+n-m$
equations as described in the statement.
4 Proof of Theorem 1.1
The proof of Theorem 1.1 consists of three cases. Namely, when the lattice
![]() $\Omega $
is closed under complex conjugation (a real lattice), when it is isogenous to its conjugate and when it is not. The method for each of these cases is essentially the same and here we give the proof in the case when
$\Omega $
is closed under complex conjugation (a real lattice), when it is isogenous to its conjugate and when it is not. The method for each of these cases is essentially the same and here we give the proof in the case when
![]() $\Omega $
is a real lattice. The differences between the proof of the real lattice case and the other two cases are explained at the end of this section.
$\Omega $
is a real lattice. The differences between the proof of the real lattice case and the other two cases are explained at the end of this section.
Assume that
![]() $\Omega $
is a real lattice. Then the restriction
$\Omega $
is a real lattice. Then the restriction
![]() $\wp |_I$
is a real-valued function, this can be seen in Section 18 in [Reference Du Val7]. From the differential equation it is clear that the structures
$\wp |_I$
is a real-valued function, this can be seen in Section 18 in [Reference Du Val7]. From the differential equation it is clear that the structures
![]() $(\overline {\mathbb {R}},\wp |_I)$
and
$(\overline {\mathbb {R}},\wp |_I)$
and
![]() $(\overline {\mathbb {R}},\wp |_I,\wp '|_I)$
are the same in the sense of having the same definable sets and it therefore suffices to prove the theorem using the structure
$(\overline {\mathbb {R}},\wp |_I,\wp '|_I)$
are the same in the sense of having the same definable sets and it therefore suffices to prove the theorem using the structure
![]() $(\overline {\mathbb {R}},\wp |_I,\wp '|_I)$
. By Gabrielov’s theorem, Theorem 3.7, this structure is model complete. Model completeness results involving the
$(\overline {\mathbb {R}},\wp |_I,\wp '|_I)$
. By Gabrielov’s theorem, Theorem 3.7, this structure is model complete. Model completeness results involving the
![]() $\wp $
-function are also due to Bianconi in [Reference Bianconi1]. However these results deal with complex functions rather than their restrictions to a real interval and therefore do not seem applicable here.
$\wp $
-function are also due to Bianconi in [Reference Bianconi1]. However these results deal with complex functions rather than their restrictions to a real interval and therefore do not seem applicable here.
If
![]() $n>1$
then we can fix all the variables except one and apply the
$n>1$
then we can fix all the variables except one and apply the
![]() $n=1$
case for each variable in turn. Therefore each coordinate function of f is semialgebraic and holomorphic and so f is an algebraic function in each variable and by Theorem 2 in [Reference Sharipov and Sukhov18] the function f is itself algebraic and therefore definable in
$n=1$
case for each variable in turn. Therefore each coordinate function of f is semialgebraic and holomorphic and so f is an algebraic function in each variable and by Theorem 2 in [Reference Sharipov and Sukhov18] the function f is itself algebraic and therefore definable in
![]() $\overline {\mathbb {R}}$
. Hence we may assume that
$\overline {\mathbb {R}}$
. Hence we may assume that
![]() $n=1.$
$n=1.$
Assume for a contradiction that v is not definable in
![]() $\overline {\mathbb {R}}$
. The proof of the following claim is a straightforward application of the identities for the real and imaginary parts of a complex function and so we simply state this claim. This corresponds to Claim 1 in the proof of Theorem 4 in [Reference Bianconi3].
$\overline {\mathbb {R}}$
. The proof of the following claim is a straightforward application of the identities for the real and imaginary parts of a complex function and so we simply state this claim. This corresponds to Claim 1 in the proof of Theorem 4 in [Reference Bianconi3].
Claim 4.1. The function
![]() $u(x,y)$
is not definable in
$u(x,y)$
is not definable in
![]() $\overline {\mathbb {R}}$
. In fact the functions
$\overline {\mathbb {R}}$
. In fact the functions
![]() $x,y,u(x,y),\ v(x,y)$
are algebraically independent over
$x,y,u(x,y),\ v(x,y)$
are algebraically independent over
![]() $\mathbb {R}$
.
$\mathbb {R}$
.
By applying the addition formula for
![]() $\wp $
we may translate and shrink the interval I and assume that
$\wp $
we may translate and shrink the interval I and assume that
![]() $I\subseteq [0,1]$
. Similarly we may replace D with a smaller disc and assume that
$I\subseteq [0,1]$
. Similarly we may replace D with a smaller disc and assume that
![]() $D\subseteq I^2\subseteq [0,1]^2$
. If f is algebraic on this smaller disc it will be algebraic on the original disc and it therefore suffices to prove the theorem on the smaller disc. The images of u and v restricted to this disc will be bounded and by a final translating and scaling we may suppose that these images are contained in the interval I.
$D\subseteq I^2\subseteq [0,1]^2$
. If f is algebraic on this smaller disc it will be algebraic on the original disc and it therefore suffices to prove the theorem on the smaller disc. The images of u and v restricted to this disc will be bounded and by a final translating and scaling we may suppose that these images are contained in the interval I.
Let
![]() $f_2(x,y)=u(x,y)$
and
$f_2(x,y)=u(x,y)$
and
![]() $f_3(x,y)=v(x,y)$
. By Proposition 3.10, for some integer
$f_3(x,y)=v(x,y)$
. By Proposition 3.10, for some integer
![]() $n\ge 1$
and an open box
$n\ge 1$
and an open box
![]() $B\subseteq D$
there are polynomials
$B\subseteq D$
there are polynomials
![]() $P_2,\dots ,P_n\in \mathbb {R}[y_0,\dots ,y_{3n+2}]$
and non-zero rationals
$P_2,\dots ,P_n\in \mathbb {R}[y_0,\dots ,y_{3n+2}]$
and non-zero rationals
![]() $a_0,\dots ,a_n$
, certain functions
$a_0,\dots ,a_n$
, certain functions
![]() $f_4,\dots ,f_n:B\rightarrow I$
, such that for all
$f_4,\dots ,f_n:B\rightarrow I$
, such that for all
![]() $(x,y)\in B$
,
$(x,y)\in B$
,
 $$ \begin{align*}\begin{array}{ccc} F_2(x,y,f_2(x,y),\dots,f_n(x,y))=0,\\\vdots\\F_n(x,y,f_2(x,y),\dots,f_n(x,y))=0, \end{array}\end{align*} $$
$$ \begin{align*}\begin{array}{ccc} F_2(x,y,f_2(x,y),\dots,f_n(x,y))=0,\\\vdots\\F_n(x,y,f_2(x,y),\dots,f_n(x,y))=0, \end{array}\end{align*} $$
and
 $$ \begin{align*}\det\left(\frac{\partial F_i}{\partial x_j}\right)_{\substack{i=2,\dots,n\\j=2,\dots,n}}(x,y,f_2(x,y),\dots,f_n(x,y))\ne 0,\end{align*} $$
$$ \begin{align*}\det\left(\frac{\partial F_i}{\partial x_j}\right)_{\substack{i=2,\dots,n\\j=2,\dots,n}}(x,y,f_2(x,y),\dots,f_n(x,y))\ne 0,\end{align*} $$
where for
![]() $i=2,\dots ,n$
we have that
$i=2,\dots ,n$
we have that
Therefore for all
![]() $i,j=2,\dots ,n$
$i,j=2,\dots ,n$
 $$ \begin{align}\frac{\partial F_i}{\partial x_j}(x_0,\dots,x_n)=\frac{\partial P_i}{\partial y_j}(\bar{y})+a_j\wp'(a_jy_j)\frac{\partial P_i}{\partial y_{j+n+1}}(\bar{y})+a_j\wp"(a_jy_j)\frac{\partial P_i}{\partial y_{j+2n+2}}(\bar{y}), \end{align} $$
$$ \begin{align}\frac{\partial F_i}{\partial x_j}(x_0,\dots,x_n)=\frac{\partial P_i}{\partial y_j}(\bar{y})+a_j\wp'(a_jy_j)\frac{\partial P_i}{\partial y_{j+n+1}}(\bar{y})+a_j\wp"(a_jy_j)\frac{\partial P_i}{\partial y_{j+2n+2}}(\bar{y}), \end{align} $$
where
Let
![]() $f_0(x,y)=x$
and
$f_0(x,y)=x$
and
![]() $f_1(x,y)=y$
. Now n is taken to be minimal such that there exists an open box B, some non-zero rationals
$f_1(x,y)=y$
. Now n is taken to be minimal such that there exists an open box B, some non-zero rationals
![]() $a_0,\dots ,a_n$
and polynomials
$a_0,\dots ,a_n$
and polynomials
![]() $P_2,\dots ,P_n$
in
$P_2,\dots ,P_n$
in
![]() $3n+3$
variables and
$3n+3$
variables and
![]() $F_i(x_0,\dots ,x_n)=P_i(x_0,\dots ,x_n,\wp (a_0x_0),\dots ,\wp (a_nx_n),\wp '(a_0x_0),\dots ,\wp '(a_nx_n))$
and there are also some functions
$F_i(x_0,\dots ,x_n)=P_i(x_0,\dots ,x_n,\wp (a_0x_0),\dots ,\wp (a_nx_n),\wp '(a_0x_0),\dots ,\wp '(a_nx_n))$
and there are also some functions
![]() $f_4,\dots ,f_n$
whose domain is B such that
$f_4,\dots ,f_n$
whose domain is B such that
![]() $F_i(f_0(x,y),\dots ,f_n(x,y))=0$
and
$F_i(f_0(x,y),\dots ,f_n(x,y))=0$
and
![]() $\det (\partial F_i/\partial x_j)(f_0(x,y),\dots ,f_n(x,y)) \ne 0$
for all
$\det (\partial F_i/\partial x_j)(f_0(x,y),\dots ,f_n(x,y)) \ne 0$
for all
![]() $(x,y)\in B$
. The functions
$(x,y)\in B$
. The functions
![]() $f_0,\dots ,f_n$
are real analytic on a disc
$f_0,\dots ,f_n$
are real analytic on a disc
![]() $D'\subseteq B$
centred at some
$D'\subseteq B$
centred at some
![]() $\alpha =(\alpha _1,\alpha _2)\in B$
. It can easily be shown that
$\alpha =(\alpha _1,\alpha _2)\in B$
. It can easily be shown that
![]() $f_0-f_0(\alpha ),\dots ,f_n-f_n(\alpha )$
are linearly independent over
$f_0-f_0(\alpha ),\dots ,f_n-f_n(\alpha )$
are linearly independent over
![]() $\mathbb {Q}$
. Applying Theorem 2.7 to
$\mathbb {Q}$
. Applying Theorem 2.7 to
![]() $a_0f_0,\dots ,a_nf_n$
gives that
$a_0f_0,\dots ,a_nf_n$
gives that
The rest of the proof consists of finding a contradictory upper bound on this transcendence degree. Let
and
 $$ \begin{align*} \tilde{y}=\tilde{y}(x,y)=(&f_0(x,y),\dots,f_n(x,y),\wp(a_0f_0(x,y)),\dots,\wp(a_nf_n(x,y)),\\&\wp'(a_0f_0(x,y)),\dots,\wp'(a_nf_n(x,y))) \end{align*} $$
$$ \begin{align*} \tilde{y}=\tilde{y}(x,y)=(&f_0(x,y),\dots,f_n(x,y),\wp(a_0f_0(x,y)),\dots,\wp(a_nf_n(x,y)),\\&\wp'(a_0f_0(x,y)),\dots,\wp'(a_nf_n(x,y))) \end{align*} $$
for all
![]() $(x,y)\in B$
. From (4.1) it is clear that for all
$(x,y)\in B$
. From (4.1) it is clear that for all
![]() $(x,y)\in B$
$(x,y)\in B$
 $$ \begin{align*}\begin{pmatrix} \frac{\partial F_2}{\partial x_2}&\dots&\frac{\partial F_2}{\partial x_n}\\\vdots&\ddots&\vdots\\\frac{\partial F_n}{\partial x_2}&\dots&\frac{\partial F_n}{\partial x_n} \end{pmatrix}(\tilde{x}(x,y))=\begin{pmatrix} \frac{\partial P_2}{\partial y_2}&\dots&\frac{\partial P_2}{\partial y_{3n+2}}\\\vdots&\ddots&\vdots\\\frac{\partial P_n}{\partial y_2}&\dots&\frac{\partial P_n}{\partial y_{3n+2}} \end{pmatrix}(\tilde{y}(x,y))\cdot M, \end{align*} $$
$$ \begin{align*}\begin{pmatrix} \frac{\partial F_2}{\partial x_2}&\dots&\frac{\partial F_2}{\partial x_n}\\\vdots&\ddots&\vdots\\\frac{\partial F_n}{\partial x_2}&\dots&\frac{\partial F_n}{\partial x_n} \end{pmatrix}(\tilde{x}(x,y))=\begin{pmatrix} \frac{\partial P_2}{\partial y_2}&\dots&\frac{\partial P_2}{\partial y_{3n+2}}\\\vdots&\ddots&\vdots\\\frac{\partial P_n}{\partial y_2}&\dots&\frac{\partial P_n}{\partial y_{3n+2}} \end{pmatrix}(\tilde{y}(x,y))\cdot M, \end{align*} $$
where M is the
![]() $(3n+1)\times (n-1)$
matrix
$(3n+1)\times (n-1)$
matrix
 $$ \begin{align*}M=\begin{pmatrix} &0&0&&0&0&\\I_{n-1}&\vdots&\vdots& M_1&\vdots&\vdots& M_2\\&0&0&&0&0& \end{pmatrix}^T,\end{align*} $$
$$ \begin{align*}M=\begin{pmatrix} &0&0&&0&0&\\I_{n-1}&\vdots&\vdots& M_1&\vdots&\vdots& M_2\\&0&0&&0&0& \end{pmatrix}^T,\end{align*} $$
where
 $$ \begin{align*}M_1=\begin{pmatrix} a_2\wp'(a_2f_2(x,y))&\dots&0\\\vdots&\ddots&\vdots\\0 &\dots & a_n\wp'(a_nf_n(x,y)) \end{pmatrix}\end{align*} $$
$$ \begin{align*}M_1=\begin{pmatrix} a_2\wp'(a_2f_2(x,y))&\dots&0\\\vdots&\ddots&\vdots\\0 &\dots & a_n\wp'(a_nf_n(x,y)) \end{pmatrix}\end{align*} $$
and
 $$ \begin{align*}M_2=\begin{pmatrix} a_2\wp"(a_2f_2(x,y))&\dots&0\\\vdots&\ddots&\vdots\\0 & \dots & a_n\wp"(a_nf_n(x,y)) \end{pmatrix}.\end{align*} $$
$$ \begin{align*}M_2=\begin{pmatrix} a_2\wp"(a_2f_2(x,y))&\dots&0\\\vdots&\ddots&\vdots\\0 & \dots & a_n\wp"(a_nf_n(x,y)) \end{pmatrix}.\end{align*} $$
The rows of
 $$ \begin{align*}\begin{pmatrix} \partial F_2/\partial x_2&\dots&\partial F_2/\partial x_n\\\vdots&\ddots&\vdots\\\partial F_n/\partial x_2&\dots&\partial F_n/\partial x_n \end{pmatrix}(\tilde{x}(x,y))\end{align*} $$
$$ \begin{align*}\begin{pmatrix} \partial F_2/\partial x_2&\dots&\partial F_2/\partial x_n\\\vdots&\ddots&\vdots\\\partial F_n/\partial x_2&\dots&\partial F_n/\partial x_n \end{pmatrix}(\tilde{x}(x,y))\end{align*} $$
are linearly independent over
![]() $\mathbb {R}$
and so the rows of
$\mathbb {R}$
and so the rows of
 $$ \begin{align*}\begin{pmatrix} \partial P_2/\partial y_2&\dots&\partial P_2/\partial y_{3n+2}\\\vdots&\ddots&\vdots\\\partial P_n/\partial y_2&\dots&\partial P_n/\partial y_{3n+2} \end{pmatrix}(\tilde{y}(x,y))\end{align*} $$
$$ \begin{align*}\begin{pmatrix} \partial P_2/\partial y_2&\dots&\partial P_2/\partial y_{3n+2}\\\vdots&\ddots&\vdots\\\partial P_n/\partial y_2&\dots&\partial P_n/\partial y_{3n+2} \end{pmatrix}(\tilde{y}(x,y))\end{align*} $$
are also linearly independent over
![]() $\mathbb {R}$
. Therefore for all
$\mathbb {R}$
. Therefore for all
![]() $(x,y)\in B$
the matrix
$(x,y)\in B$
the matrix
 $$ \begin{align*}\begin{pmatrix} \partial P_2/\partial y_2&\dots&\partial P_2/\partial y_{3n+2}\\\vdots&\ddots&\vdots\\\partial P_n/\partial y_2&\dots&\partial P_n/\partial y_{3n+2} \end{pmatrix}(\tilde{y}(x,y))\end{align*} $$
$$ \begin{align*}\begin{pmatrix} \partial P_2/\partial y_2&\dots&\partial P_2/\partial y_{3n+2}\\\vdots&\ddots&\vdots\\\partial P_n/\partial y_2&\dots&\partial P_n/\partial y_{3n+2} \end{pmatrix}(\tilde{y}(x,y))\end{align*} $$
has maximal rank
![]() $n-1$
. Given Proposition 5.3 in Chapter 8 of [Reference Lang12] it follows by a standard argument that
$n-1$
. Given Proposition 5.3 in Chapter 8 of [Reference Lang12] it follows by a standard argument that
In order to obtain the desired contradictory upper bound
![]() $n+3$
polynomial equations shall be added to the system and it shall be shown how this lowers the upper bound on transcendence degree. The first
$n+3$
polynomial equations shall be added to the system and it shall be shown how this lowers the upper bound on transcendence degree. The first
![]() $n+1$
of these equations correspond to the differential equation for the
$n+1$
of these equations correspond to the differential equation for the
![]() $\wp $
-function in each of the
$\wp $
-function in each of the
![]() $n+1$
variables and the final two of these equations arises from the Cauchy–Riemann equations for the functions u and v. For each
$n+1$
variables and the final two of these equations arises from the Cauchy–Riemann equations for the functions u and v. For each
![]() $i=0,\dots ,n$
define
$i=0,\dots ,n$
define
For all
![]() $(x,y)\in B$
and
$(x,y)\in B$
and
![]() $i=0,\dots ,n$
$i=0,\dots ,n$
By differentiating and using (2.2) it can be shown that for all
![]() $i=0,\dots ,n$
and
$i=0,\dots ,n$
and
![]() $(x,y)\in B$
,
$(x,y)\in B$
,
 $$ \begin{align*} \frac{\partial P_{i+n+1}}{\partial y_j}(y_{j+n+1},y_{j+2n+2})&+a_j\wp'(a_jf_j(x,y))\frac{\partial P_{i+n+1}}{\partial y_{j+n+1}}(y_{j+n+1},y_{j+2n+2})\\&+a_j\wp"(a_jf_j(x,y))\frac{\partial P_{i+n+1}}{\partial y_{j+2n+2}}(y_{j+n+1},y_{j+2n+2})=0. \end{align*} $$
$$ \begin{align*} \frac{\partial P_{i+n+1}}{\partial y_j}(y_{j+n+1},y_{j+2n+2})&+a_j\wp'(a_jf_j(x,y))\frac{\partial P_{i+n+1}}{\partial y_{j+n+1}}(y_{j+n+1},y_{j+2n+2})\\&+a_j\wp"(a_jf_j(x,y))\frac{\partial P_{i+n+1}}{\partial y_{j+2n+2}}(y_{j+n+1},y_{j+2n+2})=0. \end{align*} $$
It can then easily be shown that the matrix
 $$ \begin{align*}\begin{pmatrix} \partial P_2/\partial y_2&\dots&\partial P_2/\partial y_{3n+2}\\\vdots&\ddots&\vdots\\\partial P_{2n+1}/\partial y_2&\dots&\partial P_{2n+1}/\partial y_{3n+2} \end{pmatrix}(\tilde{y}(x,y))\end{align*} $$
$$ \begin{align*}\begin{pmatrix} \partial P_2/\partial y_2&\dots&\partial P_2/\partial y_{3n+2}\\\vdots&\ddots&\vdots\\\partial P_{2n+1}/\partial y_2&\dots&\partial P_{2n+1}/\partial y_{3n+2} \end{pmatrix}(\tilde{y}(x,y))\end{align*} $$
has maximal rank
![]() $2n$
and therefore by the same standard argument we have that
$2n$
and therefore by the same standard argument we have that
By the implicit function theorem the derivatives of
![]() $f_i(x_0,x_1)$
for
$f_i(x_0,x_1)$
for
![]() $i=2,\dots ,n$
are given by
$i=2,\dots ,n$
are given by
 $$ \begin{align*}\begin{pmatrix} \frac{\partial f_2}{\partial x_k}\\\vdots\\\frac{\partial f_n}{\partial x_k} \end{pmatrix}=-\Delta^{-1}\begin{pmatrix} \frac{\partial F_2}{\partial x_k}\\\vdots\\\frac{\partial F_n}{\partial x_k} \end{pmatrix},\end{align*} $$
$$ \begin{align*}\begin{pmatrix} \frac{\partial f_2}{\partial x_k}\\\vdots\\\frac{\partial f_n}{\partial x_k} \end{pmatrix}=-\Delta^{-1}\begin{pmatrix} \frac{\partial F_2}{\partial x_k}\\\vdots\\\frac{\partial F_n}{\partial x_k} \end{pmatrix},\end{align*} $$
where
![]() $k=0,1$
and
$k=0,1$
and
![]() $\Delta =(\partial F_i/\partial x_j)$
and the right-hand side is evaluated at
$\Delta =(\partial F_i/\partial x_j)$
and the right-hand side is evaluated at
![]() $(x_0,\dots ,x_n)=(f_0,\dots ,f_n)$
. Multiplying both sides by the determinant of
$(x_0,\dots ,x_n)=(f_0,\dots ,f_n)$
. Multiplying both sides by the determinant of
![]() $\Delta $
and using the Cauchy–Riemann equations for
$\Delta $
and using the Cauchy–Riemann equations for
![]() $f_2$
and
$f_2$
and
![]() $f_3$
gives two new equations
$f_3$
gives two new equations
![]() $F_0$
and
$F_0$
and
![]() $F_1$
with corresponding polynomials
$F_1$
with corresponding polynomials
![]() $P_0$
and
$P_0$
and
![]() $P_1$
, following the method of Bianconi in [Reference Bianconi3]. These are of the form,
$P_1$
, following the method of Bianconi in [Reference Bianconi3]. These are of the form,
 $$ \begin{align*} F_0=[& \text{first line of }-\det\Delta\cdot(\Delta^{-1}(\partial F_i/\partial x_0))\\& \text{ minus the second line of }-\det\Delta\cdot(\Delta^{-1}(\partial F_i/\partial x_1))] \end{align*} $$
$$ \begin{align*} F_0=[& \text{first line of }-\det\Delta\cdot(\Delta^{-1}(\partial F_i/\partial x_0))\\& \text{ minus the second line of }-\det\Delta\cdot(\Delta^{-1}(\partial F_i/\partial x_1))] \end{align*} $$
and
 $$ \begin{align*} F_1=[& \text{first line of }-\det\Delta\cdot(\Delta^{-1}(\partial F_i/\partial x_1))\\& \text{ plus the second line of }-\det\Delta\cdot(\Delta^{-1}(\partial F_i/\partial x_0))]. \end{align*} $$
$$ \begin{align*} F_1=[& \text{first line of }-\det\Delta\cdot(\Delta^{-1}(\partial F_i/\partial x_1))\\& \text{ plus the second line of }-\det\Delta\cdot(\Delta^{-1}(\partial F_i/\partial x_0))]. \end{align*} $$
In order to lower the upper bound further we have the following lemma, the proof of which adapts those of Claims 5 and 6 in the proof of Theorem 4 in [Reference Bianconi3].
Lemma 4.2. For each
![]() $k=0,1$
there is a point
$k=0,1$
there is a point
![]() $z\in \mathbb {C}^{3n+3}$
such that
$z\in \mathbb {C}^{3n+3}$
such that
![]() $P_k(z)\ne 0$
and
$P_k(z)\ne 0$
and
![]() $P_{1-k}(z)=0$
and
$P_{1-k}(z)=0$
and
![]() $P_i(z)=0$
for all
$P_i(z)=0$
for all
![]() $i=2,\dots ,2n+1$
.
$i=2,\dots ,2n+1$
.
Proof This adapts the proofs of Claims 5 and 6 in the proof of Theorem 4 in [Reference Bianconi3]. Let V be the subset of
![]() $\mathbb {R}^{3n+3}$
defined by
$\mathbb {R}^{3n+3}$
defined by
where
![]() $\wp (ax)=(\wp (a_0x_0),\dots ,\wp (a_nx_n))$
and
$\wp (ax)=(\wp (a_0x_0),\dots ,\wp (a_nx_n))$
and
![]() $\wp '(ax)=(\wp '(a_0x_0),\dots ,\wp '(a_nx_n))$
. Also let W be the subset of
$\wp '(ax)=(\wp '(a_0x_0),\dots ,\wp '(a_nx_n))$
. Also let W be the subset of
![]() $\mathbb {R}^{3n+3}$
defined by
$\mathbb {R}^{3n+3}$
defined by
 $$ \begin{align*}W=\{&z\in\mathbb{R}^{3n+3}:P_2(z)=0,\dots,P_{2n+1}(z)=0 \text{ and }(\partial P_i/\partial y_j)(z)\ne 0\\& \text{ for }i=2,\dots,2n+1,j=2,\dots,3n+2 \text{ has maximal rank }\}.\end{align*} $$
$$ \begin{align*}W=\{&z\in\mathbb{R}^{3n+3}:P_2(z)=0,\dots,P_{2n+1}(z)=0 \text{ and }(\partial P_i/\partial y_j)(z)\ne 0\\& \text{ for }i=2,\dots,2n+1,j=2,\dots,3n+2 \text{ has maximal rank }\}.\end{align*} $$
Let X be the subset of
![]() $\mathbb {R}^{3n+3}$
defined by
$\mathbb {R}^{3n+3}$
defined by
![]() $\{ \tilde {y}(x,y)|(x,y)\in B \}$
. Then it is clear that
$\{ \tilde {y}(x,y)|(x,y)\in B \}$
. Then it is clear that
![]() $X\subseteq V\cap W$
.
$X\subseteq V\cap W$
.
The subset V may also be written as
where for
![]() $i=0,\dots ,n$
$i=0,\dots ,n$
 $$ \begin{align*} &\widehat{F}_i(x,y,z)=y_i-\wp(a_ix_i), \\ &\widehat{F}_{i+n+1}(x,y,z)=z_i-\wp'(a_ix_i). \end{align*} $$
$$ \begin{align*} &\widehat{F}_i(x,y,z)=y_i-\wp(a_ix_i), \\ &\widehat{F}_{i+n+1}(x,y,z)=z_i-\wp'(a_ix_i). \end{align*} $$
We denote the Jacobian matrix for this system by
![]() $\Phi $
and this is a
$\Phi $
and this is a
![]() ${(2n\kern1.3pt{+}\kern1.3pt2)\kern1.3pt{\times}\kern1.3pt (3n\kern1.3pt{+}\kern1.3pt3)}$
matrix given by
${(2n\kern1.3pt{+}\kern1.3pt2)\kern1.3pt{\times}\kern1.3pt (3n\kern1.3pt{+}\kern1.3pt3)}$
matrix given by
 $$ \begin{align*}\Phi=\begin{pmatrix} -a_0\wp'(a_0x_0)&\dots&0&1&\dots&0&0&\dots&0\\ \vdots&\ddots&\vdots&\vdots&\ddots&\vdots&\vdots&\ddots&\vdots \\ 0&\dots&-a_n\wp'(a_nx_n)&0&\dots&1&0&\dots&0 \\ -a_0\wp"(a_0x_0)&\dots&0&0&\dots&0&1&\dots&0\\ \vdots&\ddots&\vdots&\vdots&\ddots&\vdots&\vdots&\ddots&\vdots \\ 0&\dots&-a_n\wp"(a_nx_n)&0&\dots&0&0&\dots&1 \end{pmatrix}.\end{align*} $$
$$ \begin{align*}\Phi=\begin{pmatrix} -a_0\wp'(a_0x_0)&\dots&0&1&\dots&0&0&\dots&0\\ \vdots&\ddots&\vdots&\vdots&\ddots&\vdots&\vdots&\ddots&\vdots \\ 0&\dots&-a_n\wp'(a_nx_n)&0&\dots&1&0&\dots&0 \\ -a_0\wp"(a_0x_0)&\dots&0&0&\dots&0&1&\dots&0\\ \vdots&\ddots&\vdots&\vdots&\ddots&\vdots&\vdots&\ddots&\vdots \\ 0&\dots&-a_n\wp"(a_nx_n)&0&\dots&0&0&\dots&1 \end{pmatrix}.\end{align*} $$
The normal space to V at a point is generated by the rows of
![]() $\Phi $
evaluated at this point. Recall the matrix M,
$\Phi $
evaluated at this point. Recall the matrix M,
 $$ \begin{align*}M=\begin{pmatrix} & 0&0& &0&0&\\I_{n-1}&\vdots&\vdots& M_1&\vdots&\vdots & M_2\\& 0&0&&0&0& \end{pmatrix}^T,\end{align*} $$
$$ \begin{align*}M=\begin{pmatrix} & 0&0& &0&0&\\I_{n-1}&\vdots&\vdots& M_1&\vdots&\vdots & M_2\\& 0&0&&0&0& \end{pmatrix}^T,\end{align*} $$
where
 $$ \begin{align*}M_1=\begin{pmatrix} a_2\wp'(a_2f_2(x,y))&\dots&0\\\vdots&\ddots&\vdots\\0& \dots & a_n\wp'(a_nf_n(x,y)) \end{pmatrix}\end{align*} $$
$$ \begin{align*}M_1=\begin{pmatrix} a_2\wp'(a_2f_2(x,y))&\dots&0\\\vdots&\ddots&\vdots\\0& \dots & a_n\wp'(a_nf_n(x,y)) \end{pmatrix}\end{align*} $$
and
 $$ \begin{align*}M_2=\begin{pmatrix} a_2\wp"(a_2f_2(x,y))&\dots&0\\\vdots&\ddots&\vdots\\0&\dots & a_n\wp"(a_nf_n(x,y)) \end{pmatrix}.\end{align*} $$
$$ \begin{align*}M_2=\begin{pmatrix} a_2\wp"(a_2f_2(x,y))&\dots&0\\\vdots&\ddots&\vdots\\0&\dots & a_n\wp"(a_nf_n(x,y)) \end{pmatrix}.\end{align*} $$
Let
![]() $M'$
be the matrix
$M'$
be the matrix
 $$ \begin{align*}M'=\begin{pmatrix} 0&0&\\\vdots&\vdots & M^T\\0&0& \end{pmatrix}.\end{align*} $$
$$ \begin{align*}M'=\begin{pmatrix} 0&0&\\\vdots&\vdots & M^T\\0&0& \end{pmatrix}.\end{align*} $$
Then the matrix product
![]() $M'\cdot (\Phi (\tilde {y}))^T$
gives the
$M'\cdot (\Phi (\tilde {y}))^T$
gives the
![]() $(n-1)\times (2n+2)$
zero matrix. Therefore the kernel of the linear transformation from
$(n-1)\times (2n+2)$
zero matrix. Therefore the kernel of the linear transformation from
![]() $\mathbb {R}^{3n+3}$
to
$\mathbb {R}^{3n+3}$
to
![]() $\mathbb {R}^{2n+2}$
given by the matrix
$\mathbb {R}^{2n+2}$
given by the matrix
![]() $M'$
is generated by the rows of the matrix
$M'$
is generated by the rows of the matrix
![]() $\Phi (\tilde {y})$
. Let P be the matrix
$\Phi (\tilde {y})$
. Let P be the matrix
 $$ \begin{align*}P=\begin{pmatrix} \partial P_2/\partial y_0&\dots&\partial P_n/\partial y_0\\\vdots&\ddots&\vdots\\\partial P_2/\partial y_{3n+2}&\dots&\partial P_n/\partial y_{3n+2} \end{pmatrix}(\tilde{y}).\end{align*} $$
$$ \begin{align*}P=\begin{pmatrix} \partial P_2/\partial y_0&\dots&\partial P_n/\partial y_0\\\vdots&\ddots&\vdots\\\partial P_2/\partial y_{3n+2}&\dots&\partial P_n/\partial y_{3n+2} \end{pmatrix}(\tilde{y}).\end{align*} $$
Then we have that
 $$ \begin{align*}M'\cdot P=\begin{pmatrix} \partial F_2/\partial x_2&\dots&\partial F_n/\partial x_2\\\vdots&\ddots&\vdots\\\partial F_2/\partial x_n&\dots&\partial F_n/\partial x_n \end{pmatrix}(\tilde{x}).\end{align*} $$
$$ \begin{align*}M'\cdot P=\begin{pmatrix} \partial F_2/\partial x_2&\dots&\partial F_n/\partial x_2\\\vdots&\ddots&\vdots\\\partial F_2/\partial x_n&\dots&\partial F_n/\partial x_n \end{pmatrix}(\tilde{x}).\end{align*} $$
The columns of the matrix on the right-hand side of this equation are linearly independent over
![]() $\mathbb {R}$
. Therefore the subspace of
$\mathbb {R}$
. Therefore the subspace of
![]() $\mathbb {R}^{3n+3}$
generated by the columns of P has trivial intersection with the kernel of the linear transformation given by
$\mathbb {R}^{3n+3}$
generated by the columns of P has trivial intersection with the kernel of the linear transformation given by
![]() $M'.$
As the normal space to W at a point is generated by the columns of P evaluated at this point we have that in particular the normal spaces to V and W at each point in X have trivial intersection and so the intersection of V and W is transversal.
$M'.$
As the normal space to W at a point is generated by the columns of P evaluated at this point we have that in particular the normal spaces to V and W at each point in X have trivial intersection and so the intersection of V and W is transversal.
Therefore if the subspace V is shifted locally then the intersection of V and W is still transversal. We shall now give such a shift explicitly. For real numbers
![]() $\eta $
and
$\eta $
and
![]() $\xi $
we let
$\xi $
we let
![]() $V_{\eta ,\xi }$
be the subset given by applying the following operations to V. In other words
$V_{\eta ,\xi }$
be the subset given by applying the following operations to V. In other words
![]() $V_{\eta ,\xi }=\Psi (V)$
for
$V_{\eta ,\xi }=\Psi (V)$
for
![]() $ \Psi :\mathbb {R}^{3n+3}\rightarrow \mathbb {R}^{3n+3}$
where
$ \Psi :\mathbb {R}^{3n+3}\rightarrow \mathbb {R}^{3n+3}$
where
![]() $\Psi $
does the following, for
$\Psi $
does the following, for
![]() $(y_0,\dots ,y_{3n+2})\in \mathbb {R}^{3n+3}$
$(y_0,\dots ,y_{3n+2})\in \mathbb {R}^{3n+3}$
 $$ \begin{align*} & y_2\mapsto y_2+\eta y_0+\xi y_1 \\& y_{2+n+1}\mapsto\frac{1}{4}\left(\frac{y_{2+2n+2}-\wp^\prime(a_2(\eta y_0+\xi y_1))}{y_{2+n+1}-\wp(a_2(\eta y_0+\xi y_1))}\right)^2-y_{2+n+1}-\wp(a_2(\eta y_0+\xi y_1)) \end{align*} $$
$$ \begin{align*} & y_2\mapsto y_2+\eta y_0+\xi y_1 \\& y_{2+n+1}\mapsto\frac{1}{4}\left(\frac{y_{2+2n+2}-\wp^\prime(a_2(\eta y_0+\xi y_1))}{y_{2+n+1}-\wp(a_2(\eta y_0+\xi y_1))}\right)^2-y_{2+n+1}-\wp(a_2(\eta y_0+\xi y_1)) \end{align*} $$
and
 $$ \begin{align*}&y_{2+2n+2}\mapsto \frac{\begin{matrix} \Big( \wp(a_2(\eta y_0+\xi y_1))y_{2+2n+2}-\wp'(a_2(\eta y_0+\xi y_1))y_{2+n+1}\\-\wp(a_2(y_2+\eta y_0+\xi y_1))(y_{2+2n+2}-\wp'(a_2(\eta y_0+\xi y_1))\Big) \end{matrix}}{y_{2+n+1}-\wp(a_2(\eta y_0+\xi y_1))} \end{align*} $$
$$ \begin{align*}&y_{2+2n+2}\mapsto \frac{\begin{matrix} \Big( \wp(a_2(\eta y_0+\xi y_1))y_{2+2n+2}-\wp'(a_2(\eta y_0+\xi y_1))y_{2+n+1}\\-\wp(a_2(y_2+\eta y_0+\xi y_1))(y_{2+2n+2}-\wp'(a_2(\eta y_0+\xi y_1))\Big) \end{matrix}}{y_{2+n+1}-\wp(a_2(\eta y_0+\xi y_1))} \end{align*} $$
and the rest of the variables are fixed. The projection of W onto the variables
![]() $y_0,y_1,y_2,y_3$
contains the set
$y_0,y_1,y_2,y_3$
contains the set
in its interior. If it did not then as
![]() $\dim \pi W=4$
we have
$\dim \pi W=4$
we have
![]() $\dim \partial W\le 3$
and so there is an algebraic relation between
$\dim \partial W\le 3$
and so there is an algebraic relation between
![]() $f_0,f_1,f_2$
and
$f_0,f_1,f_2$
and
![]() $f_3$
contradicting Claim 4.1. So for each real
$f_3$
contradicting Claim 4.1. So for each real
![]() $\eta $
and
$\eta $
and
![]() $\xi $
there is a positive real number
$\xi $
there is a positive real number
![]() $\delta $
such that for all real
$\delta $
such that for all real
![]() $f_0$
and
$f_0$
and
![]() $f_1$
with
$f_1$
with
![]() $f_0^2+f_1^2<\delta ^2$
the intersection of X with
$f_0^2+f_1^2<\delta ^2$
the intersection of X with
![]() $V_{\eta ,\xi }$
is non-empty. The effect of
$V_{\eta ,\xi }$
is non-empty. The effect of
![]() $\Psi $
on the subset X is the following:
$\Psi $
on the subset X is the following:
 $$ \begin{align*} &f_2\rightarrow f_2+\eta f_0+\xi f_1, \\ & \wp(a_2f_2)\rightarrow \wp(a_2(f_2+\eta f_0+\xi f_1)), \\& \wp'(a_2f_2)\rightarrow \wp'(a_2(f_2+\eta f_0+\xi f_1)). \end{align*} $$
$$ \begin{align*} &f_2\rightarrow f_2+\eta f_0+\xi f_1, \\ & \wp(a_2f_2)\rightarrow \wp(a_2(f_2+\eta f_0+\xi f_1)), \\& \wp'(a_2f_2)\rightarrow \wp'(a_2(f_2+\eta f_0+\xi f_1)). \end{align*} $$
The real numbers
![]() $\eta $
and
$\eta $
and
![]() $\xi $
may be chosen so that at least one of the Cauchy–Riemann equations for u and v are not satisfied. Therefore there is a point
$\xi $
may be chosen so that at least one of the Cauchy–Riemann equations for u and v are not satisfied. Therefore there is a point
![]() $z\in \mathbb {R}^{3n+3}$
such that
$z\in \mathbb {R}^{3n+3}$
such that
![]() $P_k(z)\ne 0$
for some
$P_k(z)\ne 0$
for some
![]() $k=0,1$
and
$k=0,1$
and
![]() $P_{1-k}(z)=P_j(z)=0$
for
$P_{1-k}(z)=P_j(z)=0$
for
![]() $j=2,\dots ,2n+1$
and so the lemma is proved.
$j=2,\dots ,2n+1$
and so the lemma is proved.
By shrinking and shifting the disc D if necessary we may assume that all the points
 $$ \begin{align*} \tilde{y}(x,y)=(&x,y,f_2(x,y),\dots,f_n(x,y),\\&\wp(a_0x),\wp(a_1y),\wp(a_2f_2(x,y)), \dots,\wp(a_nf_n(x,y)),\\&\wp'(a_0x),\wp'(a_1y),\wp'(a_2f_2(x,y)),\dots,\wp'(a_nf_n(x,y))) \end{align*} $$
$$ \begin{align*} \tilde{y}(x,y)=(&x,y,f_2(x,y),\dots,f_n(x,y),\\&\wp(a_0x),\wp(a_1y),\wp(a_2f_2(x,y)), \dots,\wp(a_nf_n(x,y)),\\&\wp'(a_0x),\wp'(a_1y),\wp'(a_2f_2(x,y)),\dots,\wp'(a_nf_n(x,y))) \end{align*} $$
such that the system
![]() $P_2(\tilde {y})=\dots =P_{2n+1}(\tilde {y})=0$
is satisfied are contained in a single irreducible component of the variety
$P_2(\tilde {y})=\dots =P_{2n+1}(\tilde {y})=0$
is satisfied are contained in a single irreducible component of the variety
![]() $\mathcal {V}(\langle P_2,\dots ,P_{2n+1}\rangle )$
denoted
$\mathcal {V}(\langle P_2,\dots ,P_{2n+1}\rangle )$
denoted
![]() $\mathcal {W}$
. Suppose that
$\mathcal {W}$
. Suppose that
![]() $\dim (\mathcal {W}\cap \mathcal {V}(\langle P_0\rangle ))=\dim \mathcal {W}$
. Then
$\dim (\mathcal {W}\cap \mathcal {V}(\langle P_0\rangle ))=\dim \mathcal {W}$
. Then
![]() $\mathcal {W}\cap \mathcal {V}(\langle P_0\rangle )=\mathcal {W}$
as
$\mathcal {W}\cap \mathcal {V}(\langle P_0\rangle )=\mathcal {W}$
as
![]() $\mathcal {W}$
is irreducible. By the proof of Lemma 4.2 there is a point
$\mathcal {W}$
is irreducible. By the proof of Lemma 4.2 there is a point
![]() $z\in \mathcal {W}$
such that
$z\in \mathcal {W}$
such that
![]() $P_2(z)=\dots =P_{2n+1}(z)=0$
and
$P_2(z)=\dots =P_{2n+1}(z)=0$
and
![]() $P_0(z)\ne 0$
. Therefore there is a point
$P_0(z)\ne 0$
. Therefore there is a point
![]() $z\in \mathcal {W}$
such that
$z\in \mathcal {W}$
such that
![]() $z\notin \mathcal {V}(P_0)$
, a contradiction. By once again shifting and shrinking the disc D we may suppose that all of the points
$z\notin \mathcal {V}(P_0)$
, a contradiction. By once again shifting and shrinking the disc D we may suppose that all of the points
![]() $\tilde {y}(x,y)$
satisfying the system
$\tilde {y}(x,y)$
satisfying the system
![]() $P_0(\tilde {y})=P_2(\tilde {y})=\dots =P_{2n+1}(\tilde {y})=0$
are contained in an irreducible component of the variety
$P_0(\tilde {y})=P_2(\tilde {y})=\dots =P_{2n+1}(\tilde {y})=0$
are contained in an irreducible component of the variety
![]() $\mathcal {V}(\langle P_0,P_2,\dots ,P_{2n+1}\rangle )$
, denoted
$\mathcal {V}(\langle P_0,P_2,\dots ,P_{2n+1}\rangle )$
, denoted
![]() $\mathcal {W}'$
.
$\mathcal {W}'$
.
Suppose that
![]() $\dim ( \mathcal {W}'\cap \mathcal {V}(\langle P_1\rangle ))=\dim \mathcal {W}'$
, then again as
$\dim ( \mathcal {W}'\cap \mathcal {V}(\langle P_1\rangle ))=\dim \mathcal {W}'$
, then again as
![]() $\mathcal {W}'$
is irreducible we have that
$\mathcal {W}'$
is irreducible we have that
![]() $\mathcal {W}'\cap \mathcal {V}(\langle P_1\rangle )=\mathcal {W}'$
. Again by the proof of Lemma 4.2 there is a point
$\mathcal {W}'\cap \mathcal {V}(\langle P_1\rangle )=\mathcal {W}'$
. Again by the proof of Lemma 4.2 there is a point
![]() $z\in \mathcal {W}$
such that only one of
$z\in \mathcal {W}$
such that only one of
![]() $P_0(z)$
and
$P_0(z)$
and
![]() $P_1(z)$
equals zero and
$P_1(z)$
equals zero and
![]() $P_2(z)=\dots =P_{2n+1}(z)=0$
. Therefore there is a point
$P_2(z)=\dots =P_{2n+1}(z)=0$
. Therefore there is a point
![]() $z\in \mathcal {W}'$
and
$z\in \mathcal {W}'$
and
![]() $z\notin \mathcal {V}(\langle P_1\rangle )$
, a contradiction as required. We have shown that if we add each of the polynomials
$z\notin \mathcal {V}(\langle P_1\rangle )$
, a contradiction as required. We have shown that if we add each of the polynomials
![]() $P_0$
and
$P_0$
and
![]() $P_1$
to the system
$P_1$
to the system
![]() $P_2,\dots ,P_{2n+1}$
and consider the variety corresponding to the ideal generated by each of these new systems in turn then the dimension of each of these varieties decreases. Hence the upper bound on the transcendence degree of our finitely generated extension of
$P_2,\dots ,P_{2n+1}$
and consider the variety corresponding to the ideal generated by each of these new systems in turn then the dimension of each of these varieties decreases. Hence the upper bound on the transcendence degree of our finitely generated extension of
![]() $\mathbb {C}$
decreases by two.
$\mathbb {C}$
decreases by two.
Therefore we have a lower bound
and an upper bound
a contradiction as required.
If
![]() $\Omega $
is not a real lattice then one must consider the structure
$\Omega $
is not a real lattice then one must consider the structure
![]() $(\overline {\mathbb {R}},\mathrm {Re\,}(\wp )|_I,\mathrm {Im\,}(\wp )|_I,\\\mathrm {Re\,}(\wp ')|_I,\mathrm {Im\,}(\wp ')|_I)$
, which is also model complete by Gabrielov’s result, Corollary 3.8. The presence of the real and imaginary parts of
$(\overline {\mathbb {R}},\mathrm {Re\,}(\wp )|_I,\mathrm {Im\,}(\wp )|_I,\\\mathrm {Re\,}(\wp ')|_I,\mathrm {Im\,}(\wp ')|_I)$
, which is also model complete by Gabrielov’s result, Corollary 3.8. The presence of the real and imaginary parts of
![]() $\wp $
gives an extra
$\wp $
gives an extra
![]() $2n+2$
variables in the system of polynomial equations arising from Proposition 3.10. This raises the corresponding upper bound by
$2n+2$
variables in the system of polynomial equations arising from Proposition 3.10. This raises the corresponding upper bound by
![]() $2n+2$
. Therefore the method in the real lattice case must be adapted in order to find the required contradictory upper and lower bounds on transcendence degree. By Proposition 3.10 we have a system of polynomials involving the real and imaginary parts of both
$2n+2$
. Therefore the method in the real lattice case must be adapted in order to find the required contradictory upper and lower bounds on transcendence degree. By Proposition 3.10 we have a system of polynomials involving the real and imaginary parts of both
![]() $\wp $
and
$\wp $
and
![]() $\wp '$
, which may be rearranged to give a polynomial system involving
$\wp '$
, which may be rearranged to give a polynomial system involving
![]() $\wp ,\wp ',\tilde {\wp }$
and
$\wp ,\wp ',\tilde {\wp }$
and
![]() $\tilde {\wp }'$
where
$\tilde {\wp }'$
where
![]() $\tilde {\wp }(z)=\overline {\wp (\bar {z})}=\wp _{\overline {\Omega }}(z)$
. If
$\tilde {\wp }(z)=\overline {\wp (\bar {z})}=\wp _{\overline {\Omega }}(z)$
. If
![]() $\Omega $
is not isogenous to
$\Omega $
is not isogenous to
![]() $\overline {\Omega }$
then there are no integers
$\overline {\Omega }$
then there are no integers
![]() $a,b,c,d$
with
$a,b,c,d$
with
![]() $ad-bc\ne 0$
such that
$ad-bc\ne 0$
such that
![]() $\overline \tau =(a\tau +b)/(c\tau +d)$
and so we may apply Theorem 2.7 with the Weierstrass functions
$\overline \tau =(a\tau +b)/(c\tau +d)$
and so we may apply Theorem 2.7 with the Weierstrass functions
![]() $\wp $
and
$\wp $
and
![]() $\tilde {\wp }$
in order to obtain a higher lower bound on transcendence degree. In order to lower the corresponding upper bound on transcendence degree further we add polynomial equations corresponding to the differential equation for
$\tilde {\wp }$
in order to obtain a higher lower bound on transcendence degree. In order to lower the corresponding upper bound on transcendence degree further we add polynomial equations corresponding to the differential equation for
![]() $\tilde {\wp }$
in each variable as well as corresponding versions of the polynomial equations added in the real lattice case. This gives the desired contradiction.
$\tilde {\wp }$
in each variable as well as corresponding versions of the polynomial equations added in the real lattice case. This gives the desired contradiction.
If
![]() $\Omega $
is isogenous to its complex conjugate then there is a non-zero complex number
$\Omega $
is isogenous to its complex conjugate then there is a non-zero complex number
![]() $\alpha $
such that
$\alpha $
such that
![]() $\alpha \Omega \subseteq \overline {\Omega }$
. Therefore from the definition of
$\alpha \Omega \subseteq \overline {\Omega }$
. Therefore from the definition of
![]() $\wp $
we may rewrite
$\wp $
we may rewrite
![]() $\tilde {\wp }(z)$
as a rational function in
$\tilde {\wp }(z)$
as a rational function in
![]() $\wp (\alpha ^{-1}z)$
. The system of polynomials obtained using Proposition 3.10 may be rewritten as system of rational functions involving
$\wp (\alpha ^{-1}z)$
. The system of polynomials obtained using Proposition 3.10 may be rewritten as system of rational functions involving
![]() $\wp (z),\wp (\alpha ^{-1}z),\wp '(z)$
and
$\wp (z),\wp (\alpha ^{-1}z),\wp '(z)$
and
![]() $\wp '(\alpha ^{-1}z)$
from which a system of polynomials may be obtained. The lower bound on transcendence degree is raised by applying Theorem 2.7 with
$\wp '(\alpha ^{-1}z)$
from which a system of polynomials may be obtained. The lower bound on transcendence degree is raised by applying Theorem 2.7 with
![]() $\wp $
to the functions
$\wp $
to the functions
![]() $a_0f_0,\dots ,a_nf_n,\alpha ^{-1}a_0f_0,\dots ,\alpha ^{-1}a_nf_n$
. The upper bound on transcendence degree is lowered further by adding polynomial equations corresponding to the differential equation for
$a_0f_0,\dots ,a_nf_n,\alpha ^{-1}a_0f_0,\dots ,\alpha ^{-1}a_nf_n$
. The upper bound on transcendence degree is lowered further by adding polynomial equations corresponding to the differential equation for
![]() $\wp (\alpha ^{-1}z)$
in each variable as well as once again adding corresponding versions of the polynomial equations added in the real lattice case. This completes the proof of Theorem 1.1.
$\wp (\alpha ^{-1}z)$
in each variable as well as once again adding corresponding versions of the polynomial equations added in the real lattice case. This completes the proof of Theorem 1.1.
5 Further definability results
The first result in this section is an immediate corollary of Theorem 1.1 combined with Theorem 12.5 in [Reference Peterzil and Starchenko16].
Corollary 5.1. Let
![]() $\Omega \subseteq \mathbb {C}$
be a complex lattice which does not have complex multiplication and I be a bounded closed interval in
$\Omega \subseteq \mathbb {C}$
be a complex lattice which does not have complex multiplication and I be a bounded closed interval in
![]() $\mathbb {R}$
which does not intersect
$\mathbb {R}$
which does not intersect
![]() $\Omega $
. Let X be an analytic subset of an open set
$\Omega $
. Let X be an analytic subset of an open set
![]() $U\subseteq \mathbb {C}^n$
. Assume that U and X are definable in
$U\subseteq \mathbb {C}^n$
. Assume that U and X are definable in
![]() $(\overline {\mathbb {R}},\wp |_I)$
. Then there is a complex algebraic set
$(\overline {\mathbb {R}},\wp |_I)$
. Then there is a complex algebraic set
![]() $A\subseteq \mathbb {C}^n$
such that X is an irreducible component of
$A\subseteq \mathbb {C}^n$
such that X is an irreducible component of
![]() $A\cap U$
.
$A\cap U$
.
For real lattices the following theorem can be seen in [Reference McCulloch14]. Here the result in [Reference McCulloch14] is extended to all complex lattices and a different proof is given.
Theorem 5.2. Let
![]() $\Omega $
be a complex lattice and
$\Omega $
be a complex lattice and
![]() $I\subseteq \mathbb {R}$
a bounded closed interval such that
$I\subseteq \mathbb {R}$
a bounded closed interval such that
![]() $I\cap \Omega $
is empty. Let
$I\cap \Omega $
is empty. Let
![]() $D\subseteq \mathbb {C}$
be a disc. Then
$D\subseteq \mathbb {C}$
be a disc. Then
![]() $\wp |_D$
is definable in
$\wp |_D$
is definable in
![]() $(\overline {\mathbb {R}},\wp |_I)$
if and only if the lattice
$(\overline {\mathbb {R}},\wp |_I)$
if and only if the lattice
![]() $\Omega $
has complex multiplication.
$\Omega $
has complex multiplication.
Proof Suppose that
![]() $D\cap \Omega $
is empty. Firstly we assume that
$D\cap \Omega $
is empty. Firstly we assume that
![]() $\Omega $
has complex multiplication and so there is a non-zero complex number
$\Omega $
has complex multiplication and so there is a non-zero complex number
![]() $\alpha $
such that
$\alpha $
such that
![]() $\alpha \Omega \subseteq \Omega $
. Define
$\alpha \Omega \subseteq \Omega $
. Define
![]() $f(z)=\wp (\alpha z)$
. Then for all
$f(z)=\wp (\alpha z)$
. Then for all
![]() $\omega \in \Omega $
we have that
$\omega \in \Omega $
we have that
and so f is a meromorphic function that is periodic with respect to
![]() $\Omega $
. By Theorem 3.2 in Chapter 6 of [Reference Silverman20] the function f is a rational function in terms of
$\Omega $
. By Theorem 3.2 in Chapter 6 of [Reference Silverman20] the function f is a rational function in terms of
![]() $\wp $
and
$\wp $
and
![]() $\wp '$
. Therefore
$\wp '$
. Therefore
![]() $\wp |_{\alpha I}$
is definable in
$\wp |_{\alpha I}$
is definable in
![]() $(\overline {\mathbb {R}},\wp |_I)$
. Similarly we have that
$(\overline {\mathbb {R}},\wp |_I)$
. Similarly we have that
![]() $\wp '|_{\alpha I}$
is definable in
$\wp '|_{\alpha I}$
is definable in
![]() $(\overline {\mathbb {R}},\wp |_I)$
. We may assume that
$(\overline {\mathbb {R}},\wp |_I)$
. We may assume that
![]() $D\subseteq I \times \alpha I$
. Therefore for any
$D\subseteq I \times \alpha I$
. Therefore for any
![]() $z\in D$
we have that
$z\in D$
we have that
![]() $z=x+\alpha y$
for
$z=x+\alpha y$
for
![]() $x,y\in I$
. By the addition formula for
$x,y\in I$
. By the addition formula for
![]() $\wp $
$\wp $
for a rational function R. Therefore
![]() $\wp |_D$
is definable in
$\wp |_D$
is definable in
![]() $(\overline {\mathbb {R}},\wp |_I)$
. Conversely, suppose that
$(\overline {\mathbb {R}},\wp |_I)$
. Conversely, suppose that
![]() $\Omega $
does not have complex multiplication and that there is a disc
$\Omega $
does not have complex multiplication and that there is a disc
![]() $D\subseteq \mathbb {C}$
such that
$D\subseteq \mathbb {C}$
such that
![]() $\wp |_D$
is definable in
$\wp |_D$
is definable in
![]() $(\overline {\mathbb {R}},\wp |_I)$
. As
$(\overline {\mathbb {R}},\wp |_I)$
. As
![]() $\wp $
is holomorphic on D we have that by Theorem 1.1 the function
$\wp $
is holomorphic on D we have that by Theorem 1.1 the function
![]() $\wp |_D$
is definable in
$\wp |_D$
is definable in
![]() $\overline {\mathbb {R}}$
, a contradiction.
$\overline {\mathbb {R}}$
, a contradiction.
Now let D be a disc containing a single lattice point
![]() $\omega \in \Omega $
and consider the function
$\omega \in \Omega $
and consider the function
![]() $f(z)=(z-\omega )^2\wp (z)$
. If
$f(z)=(z-\omega )^2\wp (z)$
. If
![]() $\Omega $
has complex multiplication then as
$\Omega $
has complex multiplication then as
![]() $(z-\omega )^2 $
is definable in the structure
$(z-\omega )^2 $
is definable in the structure
![]() $(\overline {\mathbb {R}},\wp |_I)$
it is clear by a repetition of the above argument we have that
$(\overline {\mathbb {R}},\wp |_I)$
it is clear by a repetition of the above argument we have that
![]() $f|_D$
is definable in
$f|_D$
is definable in
![]() $(\overline {\mathbb {R}},\wp |_I)$
. Conversely suppose that
$(\overline {\mathbb {R}},\wp |_I)$
. Conversely suppose that
![]() $\Omega $
does not have complex multiplication and assume for a contradiction that
$\Omega $
does not have complex multiplication and assume for a contradiction that
![]() $f|_D$
is definable in the structure
$f|_D$
is definable in the structure
![]() $(\overline {\mathbb {R}},\wp |_I)$
. Then
$(\overline {\mathbb {R}},\wp |_I)$
. Then
![]() $f|_{D'}$
is definable in
$f|_{D'}$
is definable in
![]() $(\overline {\mathbb {R}},\wp |_I)$
for some disc
$(\overline {\mathbb {R}},\wp |_I)$
for some disc
![]() $D'\subseteq D$
that does not contain
$D'\subseteq D$
that does not contain
![]() $\omega $
. Therefore
$\omega $
. Therefore
![]() $\wp |_{D'}$
is definable in
$\wp |_{D'}$
is definable in
![]() $(\overline {\mathbb {R}},\wp |_I)$
, a contradiction.
$(\overline {\mathbb {R}},\wp |_I)$
, a contradiction.
In the proof of Theorem 1.1 the existence of an Ax-Schanuel statement for the Weierstrass
![]() $\wp $
-function is essential. This raises the question of whether we can recover corresponding nondefinability results for other transcendental functions that also satisfy an Ax-Schanuel theorem. In this context the modular j-function is a natural function to consider and the Ax-Schanuel result is due to Pila and Tsimerman in [Reference Pila and Tsimerman17]. The following theorem can be thought of as a j-function analogue of Theorem 5.2. The proof of this theorem adapts a similar method to the one seen in Section 4 and uses the first implicit definition in Section 3.
$\wp $
-function is essential. This raises the question of whether we can recover corresponding nondefinability results for other transcendental functions that also satisfy an Ax-Schanuel theorem. In this context the modular j-function is a natural function to consider and the Ax-Schanuel result is due to Pila and Tsimerman in [Reference Pila and Tsimerman17]. The following theorem can be thought of as a j-function analogue of Theorem 5.2. The proof of this theorem adapts a similar method to the one seen in Section 4 and uses the first implicit definition in Section 3.
Theorem 5.3. Let
![]() $I\subseteq \mathbb {R}^{>0}$
be an open interval that is bounded away from zero and let
$I\subseteq \mathbb {R}^{>0}$
be an open interval that is bounded away from zero and let
![]() $D\subseteq \mathbb {H}$
be a non-empty disc. Then the restriction of j to the disc D is not definable in the structure
$D\subseteq \mathbb {H}$
be a non-empty disc. Then the restriction of j to the disc D is not definable in the structure
![]() $(\overline {\mathbb {R}},j|_{iI})$
.
$(\overline {\mathbb {R}},j|_{iI})$
.
Proof Assume for a contradiction that there is a disc
![]() $D\subseteq \mathbb {H}$
such that the restriction
$D\subseteq \mathbb {H}$
such that the restriction
![]() $j|_D$
is definable in the structure
$j|_D$
is definable in the structure
![]() $(\overline {\mathbb {R}},j|_{iI})$
. For notational convenience we can suppose that the disc D contains the horizontal line segment
$(\overline {\mathbb {R}},j|_{iI})$
. For notational convenience we can suppose that the disc D contains the horizontal line segment
![]() $i+I$
and so the real and imaginary parts of the function
$i+I$
and so the real and imaginary parts of the function
![]() $j|_{i+I}$
are definable in the structure
$j|_{i+I}$
are definable in the structure
![]() $(\overline {\mathbb {R}},j|_{iI})$
. Rearranging the differential equation satisfied by j given in (2.6) gives that
$(\overline {\mathbb {R}},j|_{iI})$
. Rearranging the differential equation satisfied by j given in (2.6) gives that
 $$ \begin{align} ij"'(it)=\frac{-3}{2}\frac{(j"(it))^2}{ij'(it)}+\left(\frac{j^2(it)-1968j(it)+2654208}{2j^2(it)(j(it)-1728)^2}\right)(ij'(it))^3 \end{align} $$
$$ \begin{align} ij"'(it)=\frac{-3}{2}\frac{(j"(it))^2}{ij'(it)}+\left(\frac{j^2(it)-1968j(it)+2654208}{2j^2(it)(j(it)-1728)^2}\right)(ij'(it))^3 \end{align} $$
and so
![]() $ij"'(it)$
may be written as a polynomial in
$ij"'(it)$
may be written as a polynomial in
![]() $j(it),ij'(it),j"(it),(ij'(it))^{-1}$
and
$j(it),ij'(it),j"(it),(ij'(it))^{-1}$
and
![]() $(2j^2(it)(j(it)-1728)^2)^{-1}$
. By shrinking the interval I if necessary we may assume that the denominators do not vanish for any
$(2j^2(it)(j(it)-1728)^2)^{-1}$
. By shrinking the interval I if necessary we may assume that the denominators do not vanish for any
![]() $t\in I$
. Therefore by differentiating this equation with respect to t we can see that all the higher derivatives of
$t\in I$
. Therefore by differentiating this equation with respect to t we can see that all the higher derivatives of
![]() $j(it)$
may also be given as polynomials in these functions. Consider the auxiliary structure given by expanding
$j(it)$
may also be given as polynomials in these functions. Consider the auxiliary structure given by expanding
![]() $\overline {\mathbb {R}}$
by the functions
$\overline {\mathbb {R}}$
by the functions
![]() $j_B(t)=j(iB(t)),j_B'(t)=ij'(iB(t)),j_B"(t)=j"(iB(t)),j_1(t)=(ij'(B(t)))^{-1}$
and
$j_B(t)=j(iB(t)),j_B'(t)=ij'(iB(t)),j_B"(t)=j"(iB(t)),j_1(t)=(ij'(B(t)))^{-1}$
and
![]() $j_2(t)=(2j(iB(t))^2(j(iB(t))-1728)^2)^{-1\vphantom{A^A}}$
as well as B and
$j_2(t)=(2j(iB(t))^2(j(iB(t))-1728)^2)^{-1\vphantom{A^A}}$
as well as B and
![]() $B_1$
. Here
$B_1$
. Here
![]() $B:\mathbb {R}\rightarrow I$
is an algebraic function and
$B:\mathbb {R}\rightarrow I$
is an algebraic function and
![]() $B_1$
is a rational function arising from the derivative of B such that all higher derivatives of B are polynomials in B and
$B_1$
is a rational function arising from the derivative of B such that all higher derivatives of B are polynomials in B and
![]() $B_1$
. The structures
$B_1$
. The structures
![]() $(\overline {\mathbb {R}},j|_{iI})$
and
$(\overline {\mathbb {R}},j|_{iI})$
and
![]() $(\overline {\mathbb {R}},j_B,j^{\prime }_B,j^{\prime \prime }_B,j_1,j_2,B,B_1)$
are equivalent in the sense of having the same definable sets. They also have the same universally and existentially definable sets. Therefore the real and imaginary parts of the function
$(\overline {\mathbb {R}},j_B,j^{\prime }_B,j^{\prime \prime }_B,j_1,j_2,B,B_1)$
are equivalent in the sense of having the same definable sets. They also have the same universally and existentially definable sets. Therefore the real and imaginary parts of the function
![]() $j|_{i+I}$
are definable in the structure
$j|_{i+I}$
are definable in the structure
![]() $(\overline {\mathbb {R}},j_B,j^{\prime }_B,j^{\prime \prime }_B,j_1,j_2,B,B_1)$
. Therefore it suffices to prove Theorem 5.3 in this auxiliary structure. It is clear from construction that the set
$(\overline {\mathbb {R}},j_B,j^{\prime }_B,j^{\prime \prime }_B,j_1,j_2,B,B_1)$
. Therefore it suffices to prove Theorem 5.3 in this auxiliary structure. It is clear from construction that the set
![]() $\{ j_B,j^{\prime }_B,j^{\prime \prime }_B,j_1,j_2,B,B_1 \}$
is closed under differentiation and the ring of terms of this auxiliary structure is closed under differentiation in the sense of Section 3. By the Gabrielov result, Corollary 3.8, the auxiliary structure
$\{ j_B,j^{\prime }_B,j^{\prime \prime }_B,j_1,j_2,B,B_1 \}$
is closed under differentiation and the ring of terms of this auxiliary structure is closed under differentiation in the sense of Section 3. By the Gabrielov result, Corollary 3.8, the auxiliary structure
![]() $(\overline {\mathbb {R}},j_B,j^{\prime }_B,j^{\prime \prime }_B,j_1,j_2,B,B_1)$
is model complete.
$(\overline {\mathbb {R}},j_B,j^{\prime }_B,j^{\prime \prime }_B,j_1,j_2,B,B_1)$
is model complete.
Let
![]() $f_1,f_2:I\rightarrow \mathbb {R}$
be defined by
$f_1,f_2:I\rightarrow \mathbb {R}$
be defined by
![]() $f_1(t)=\mathrm {Re\,}(j(i+t))$
and
$f_1(t)=\mathrm {Re\,}(j(i+t))$
and
![]() $f_2(t)=\mathrm {Im\,}(j(i+t))$
. By applying Theorem 3.3 to both
$f_2(t)=\mathrm {Im\,}(j(i+t))$
. By applying Theorem 3.3 to both
![]() $f_1$
and
$f_1$
and
![]() $f_2$
, we have that for some integer
$f_2$
, we have that for some integer
![]() $n\ge 1$
and a subinterval
$n\ge 1$
and a subinterval
![]() $I'\subseteq I$
there are polynomials
$I'\subseteq I$
there are polynomials
![]() $P^*_1,\dots ,P^*_{n}:\mathbb {R}^{8n+8}\rightarrow \mathbb {R}$
in
$P^*_1,\dots ,P^*_{n}:\mathbb {R}^{8n+8}\rightarrow \mathbb {R}$
in
![]() $\mathbb {R}[y_1,\dots ,y_{8n+8}]$
, certain functions
$\mathbb {R}[y_1,\dots ,y_{8n+8}]$
, certain functions
![]() $f_3,\dots ,f_{n}:I'\rightarrow \mathbb {R}$
such that for all
$f_3,\dots ,f_{n}:I'\rightarrow \mathbb {R}$
such that for all
![]() $t\in I'$
,
$t\in I'$
,
 $$ \begin{align*}\begin{array}{ccc} F_1(t,f_1(t),\dots,f_{n}(t))=0\\ \vdots\\ F_n(t,f_1(t),\dots,f_{n}(t))=0\end{array}\end{align*} $$
$$ \begin{align*}\begin{array}{ccc} F_1(t,f_1(t),\dots,f_{n}(t))=0\\ \vdots\\ F_n(t,f_1(t),\dots,f_{n}(t))=0\end{array}\end{align*} $$
and
 $$ \begin{align*}\det \left(\frac{\partial F_i}{\partial x_j}\right)_{\substack{i=1,\dots,n\\j=2,\dots,n+1}}(t,f_1(t),\dots,f_{n}(t))\ne 0,\end{align*} $$
$$ \begin{align*}\det \left(\frac{\partial F_i}{\partial x_j}\right)_{\substack{i=1,\dots,n\\j=2,\dots,n+1}}(t,f_1(t),\dots,f_{n}(t))\ne 0,\end{align*} $$
where for
![]() $i=1,\dots ,n$
we have that
$i=1,\dots ,n$
we have that
 $$ \begin{align*} F_i(t,f_1(t),\dots,f_n(t))=P^*_i(&t,f_1(t),\dots,f_{n}(t), \\& j(iB(t)),j(iB(f_1(t))),\dots,j(iB(f_{n}(t))), \\& ij'(iB(t)),ij'(iB(f_1(t))),\dots,ij'(iB(f_{n}(t))), \\& j"(iB(t)),j"(iB(f_1(t))),\dots, j"(iB(f_{n}(t))), \\& j_1(t),j_1(f_1(t)),\dots,j_1(f_n(t)), \\&j_2(t),j_2(f_1(t)),\dots,j_2(f_n(t)) \\& B(t),B(f_1(t)),\dots,B(f_{n}(t)), \\& B_1(t),B_1(f_1(t)),\dots,B_1(f_{n}(t))). \end{align*} $$
$$ \begin{align*} F_i(t,f_1(t),\dots,f_n(t))=P^*_i(&t,f_1(t),\dots,f_{n}(t), \\& j(iB(t)),j(iB(f_1(t))),\dots,j(iB(f_{n}(t))), \\& ij'(iB(t)),ij'(iB(f_1(t))),\dots,ij'(iB(f_{n}(t))), \\& j"(iB(t)),j"(iB(f_1(t))),\dots, j"(iB(f_{n}(t))), \\& j_1(t),j_1(f_1(t)),\dots,j_1(f_n(t)), \\&j_2(t),j_2(f_1(t)),\dots,j_2(f_n(t)) \\& B(t),B(f_1(t)),\dots,B(f_{n}(t)), \\& B_1(t),B_1(f_1(t)),\dots,B_1(f_{n}(t))). \end{align*} $$
By the definition of the functions
![]() $j_1$
and
$j_1$
and
![]() $j_2$
as well as B and
$j_2$
as well as B and
![]() $B_1$
we may write
$B_1$
we may write
![]() $F_1,\dots ,F_n$
as algebraic functions in
$F_1,\dots ,F_n$
as algebraic functions in
![]() $t,f_1(t),\dots ,f_{n}(t),j(iB(t)),j(iB(f_1(t))),\dots , j(iB(f_{n}(t)))$
and
$t,f_1(t),\dots ,f_{n}(t),j(iB(t)),j(iB(f_1(t))),\dots , j(iB(f_{n}(t)))$
and
![]() $ij'(iB(t)),ij'(iB(f_1(t))),\dots ,ij'(iB(f_{n}(t)))$
as well as
$ij'(iB(t)),ij'(iB(f_1(t))),\dots ,ij'(iB(f_{n}(t)))$
as well as
![]() $j"(iB(t)), j"(iB(f_1(t))),\dots , j"(iB(f_{n}(t)))$
. In defining these algebraic functions square roots are introduced from the definition of B, which may affect the analyticity of these algebraic functions. The domain of these algebraic functions is a small open subset of
$j"(iB(t)), j"(iB(f_1(t))),\dots , j"(iB(f_{n}(t)))$
. In defining these algebraic functions square roots are introduced from the definition of B, which may affect the analyticity of these algebraic functions. The domain of these algebraic functions is a small open subset of
![]() $\mathbb {R}^{4n+4}$
containing the set
$\mathbb {R}^{4n+4}$
containing the set
where
![]() $f(t)=(t,f_1(t),\dots ,f_n(t))$
and the algebraic functions are taken to be analytic on this domain. Hence for
$f(t)=(t,f_1(t),\dots ,f_n(t))$
and the algebraic functions are taken to be analytic on this domain. Hence for
![]() $i=1,\dots ,n$
we have that
$i=1,\dots ,n$
we have that
 $$ \begin{align*} F_i(x_1,\dots,x_{n+1})=P_i(&x_1,\dots,x_{n+1},j(iB(x_1)),\dots,j(iB(x_{n+1})),\\& ij'(iB(x_1)),\dots,ij'(iB(x_{n+1})),j"(iB(x_1)),\dots, j"(iB(x_{n+1}))) \end{align*} $$
$$ \begin{align*} F_i(x_1,\dots,x_{n+1})=P_i(&x_1,\dots,x_{n+1},j(iB(x_1)),\dots,j(iB(x_{n+1})),\\& ij'(iB(x_1)),\dots,ij'(iB(x_{n+1})),j"(iB(x_1)),\dots, j"(iB(x_{n+1}))) \end{align*} $$
for algebraic functions
![]() $P_1,\dots ,P_n$
and in particular for all
$P_1,\dots ,P_n$
and in particular for all
![]() $t\in I'$
,
$t\in I'$
,
 $$ \begin{align*}F_i(t,f_1(t),\dots,f_{n}(t))=P_i[&t,f_1(t),\dots,f_{n}(t), \\& j(iB(t)),j(iB(f_1(t))),\dots,j(iB(f_{n}(t))), \\& ij'(iB(t)), ij'(iB(f_1(t))),\dots,ij'(iB(f_{n}(t))), \\& j"(iB(t)), j"(iB(f_1(t))),\dots, j"(iB(f_{n}(t)))]=0. \end{align*} $$
$$ \begin{align*}F_i(t,f_1(t),\dots,f_{n}(t))=P_i[&t,f_1(t),\dots,f_{n}(t), \\& j(iB(t)),j(iB(f_1(t))),\dots,j(iB(f_{n}(t))), \\& ij'(iB(t)), ij'(iB(f_1(t))),\dots,ij'(iB(f_{n}(t))), \\& j"(iB(t)), j"(iB(f_1(t))),\dots, j"(iB(f_{n}(t)))]=0. \end{align*} $$
Now take n to be minimal such that the subinterval
![]() $I'$
, the functions
$I'$
, the functions
![]() $f_3,\dots ,f_n$
and the system of algebraic functions
$f_3,\dots ,f_n$
and the system of algebraic functions
![]() $P_1,\dots ,P_n$
exists as given above. Let
$P_1,\dots ,P_n$
exists as given above. Let
 $$ \begin{align*} \tilde{y}=\tilde{y}(t)=(&t,f_1(t),\dots,f_{n}(t), \\& j(iB(t)),j(iB(f_1(t))),\dots,j(iB(f_{n}(t))), \\& ij'(iB(t)), ij'(iB(f_1(t))),\dots,ij'(iB(f_{n}(t))), \\& j"(iB(t)), j"(iB(f_1(t))),\dots, j"(iB(f_{n}(t)))). \end{align*} $$
$$ \begin{align*} \tilde{y}=\tilde{y}(t)=(&t,f_1(t),\dots,f_{n}(t), \\& j(iB(t)),j(iB(f_1(t))),\dots,j(iB(f_{n}(t))), \\& ij'(iB(t)), ij'(iB(f_1(t))),\dots,ij'(iB(f_{n}(t))), \\& j"(iB(t)), j"(iB(f_1(t))),\dots, j"(iB(f_{n}(t)))). \end{align*} $$
For all
![]() $t\in I'$
it can easily be shown that the matrix
$t\in I'$
it can easily be shown that the matrix
 $$ \begin{align*}\left( \frac{\partial P_i}{\partial y_j}\right)_{\substack{i=1,\dots,n\\j=2,\dots,4n+4}}(\tilde{y}(t))\end{align*} $$
$$ \begin{align*}\left( \frac{\partial P_i}{\partial y_j}\right)_{\substack{i=1,\dots,n\\j=2,\dots,4n+4}}(\tilde{y}(t))\end{align*} $$
has maximal rank n. The standard argument noted in the proof of Theorem 1.1 can be readily adapted for a system of algebraic functions and so
 $$ \begin{align*} \text{tr.deg}_{\mathbb{C}}\mathbb{C}[&t,f_1,\dots,f_n,\\&j(iB(t)),j(iB(f_1)),\dots,j(iB(f_n)),\\& ij^\prime(iB(t)),ij^\prime(iB(f_1)),\dots,ij^\prime(iB(f_n)),\\& j^{\prime\prime}(iB(t)),j^{\prime\prime}(iB(f_1)),\dots,j^{\prime\prime}(iB(f_n))] \le 4n+4-n=3n+4. \end{align*} $$
$$ \begin{align*} \text{tr.deg}_{\mathbb{C}}\mathbb{C}[&t,f_1,\dots,f_n,\\&j(iB(t)),j(iB(f_1)),\dots,j(iB(f_n)),\\& ij^\prime(iB(t)),ij^\prime(iB(f_1)),\dots,ij^\prime(iB(f_n)),\\& j^{\prime\prime}(iB(t)),j^{\prime\prime}(iB(f_1)),\dots,j^{\prime\prime}(iB(f_n))] \le 4n+4-n=3n+4. \end{align*} $$
Suppose that there is some integer
![]() $M\ge 1$
such that
$M\ge 1$
such that
for all
![]() $t\in I'$
, where
$t\in I'$
, where
![]() $0\le k,l\le n$
and
$0\le k,l\le n$
and
![]() $k\ne l$
and
$k\ne l$
and
![]() $f_0(t)=t$
. For convenience we assume that
$f_0(t)=t$
. For convenience we assume that
![]() $k=n-1$
and
$k=n-1$
and
![]() $n=l$
. Then
$n=l$
. Then
![]() $iB(f_n(t))$
may be written as a rational function in
$iB(f_n(t))$
may be written as a rational function in
![]() $iB(f_{n-1}(t))$
. Rearranging the modular polynomial
$iB(f_{n-1}(t))$
. Rearranging the modular polynomial
![]() $\Phi _M$
gives that
$\Phi _M$
gives that
![]() $j(iB(f_n(t)))$
may be written as an algebraic function in
$j(iB(f_n(t)))$
may be written as an algebraic function in
![]() $j(iB(f_{n-1}(t)))$
. Differentiating both sides of this equation and rearranging and repeating this process gives algebraic functions for
$j(iB(f_{n-1}(t)))$
. Differentiating both sides of this equation and rearranging and repeating this process gives algebraic functions for
![]() $ij'(iB(f_n(t)))$
and
$ij'(iB(f_n(t)))$
and
![]() $j"(iB(f_n(t)))$
in terms of
$j"(iB(f_n(t)))$
in terms of
![]() $f_{n-1}(t),j(iB(f_{n-1}(t))),ij'(iB(f_{n-1}(t)))$
and
$f_{n-1}(t),j(iB(f_{n-1}(t))),ij'(iB(f_{n-1}(t)))$
and
![]() $f_{n-1}(t),j(iB(f_{n-1}(t))),ij'(iB(f_{n-1}(t))),j"(iB(f_{n-1}(t)))$
respectively. Therefore the non-singular system of algebraic functions
$f_{n-1}(t),j(iB(f_{n-1}(t))),ij'(iB(f_{n-1}(t))),j"(iB(f_{n-1}(t)))$
respectively. Therefore the non-singular system of algebraic functions
![]() $P_1,\dots ,P_n$
may be rearranged to give a system of algebraic functions in fewer variables. If this system is non-singular at the points
$P_1,\dots ,P_n$
may be rearranged to give a system of algebraic functions in fewer variables. If this system is non-singular at the points
![]() $\tilde {y}(t)$
then there is a contradiction to the minimality of n. Therefore this system is assumed to be singular at these points. However this leads to a contradiction of the non-singularity of the original system and we may therefore conclude that no such integer
$\tilde {y}(t)$
then there is a contradiction to the minimality of n. Therefore this system is assumed to be singular at these points. However this leads to a contradiction of the non-singularity of the original system and we may therefore conclude that no such integer
![]() $M\ge 1$
exists. From this it can be shown that there is no integer
$M\ge 1$
exists. From this it can be shown that there is no integer
![]() $M\ge 1$
such that
$M\ge 1$
such that
![]() $\Phi _M(j(iB(f_k(t))),j(iB(f_l(t))))=0$
for all
$\Phi _M(j(iB(f_k(t))),j(iB(f_l(t))))=0$
for all
![]() $k,l=0,\dots ,n$
with
$k,l=0,\dots ,n$
with
![]() $k\ne l$
. Applying Theorem 2.8 to
$k\ne l$
. Applying Theorem 2.8 to
![]() $i+f_0,iB(f_0),\dots ,iB(f_n)$
gives that
$i+f_0,iB(f_0),\dots ,iB(f_n)$
gives that
 $$ \begin{align*}\text{tr.deg}_{\mathbb{C}}\mathbb{C}[&i+t,iB(t),iB(f_1),\dots,iB(f_n),\\&j(i+t),j(iB(t)),j(iB(f_1)),\dots, j(iB(f_n)), \\&j'(i+t),j'(iB(t)),j'(iB(f_1)),\dots,j'(iB(f_n)),\\&j"(i+t),j"(iB(t)), j"(iB(f_1)),\dots,j"(iB(f_n)) ]\ge 3n+7 \end{align*} $$
$$ \begin{align*}\text{tr.deg}_{\mathbb{C}}\mathbb{C}[&i+t,iB(t),iB(f_1),\dots,iB(f_n),\\&j(i+t),j(iB(t)),j(iB(f_1)),\dots, j(iB(f_n)), \\&j'(i+t),j'(iB(t)),j'(iB(f_1)),\dots,j'(iB(f_n)),\\&j"(i+t),j"(iB(t)), j"(iB(f_1)),\dots,j"(iB(f_n)) ]\ge 3n+7 \end{align*} $$
and so
 $$ \begin{align*}\text{tr.deg}_{\mathbb{C}}\mathbb{C}[&i+t,iB(t),iB(f_1),\dots,iB(f_n),\\&j(i+t),j(iB(t)),j(iB(f_1)),\dots, j(iB(f_n)), \\&j'(iB(t)),j'(iB(f_1)),\dots,j'(iB(f_n)),\\&j"(iB(t)), j"(iB(f_1)),\dots,j"(iB(f_n)) ]\ge 3n+5. \end{align*} $$
$$ \begin{align*}\text{tr.deg}_{\mathbb{C}}\mathbb{C}[&i+t,iB(t),iB(f_1),\dots,iB(f_n),\\&j(i+t),j(iB(t)),j(iB(f_1)),\dots, j(iB(f_n)), \\&j'(iB(t)),j'(iB(f_1)),\dots,j'(iB(f_n)),\\&j"(iB(t)), j"(iB(f_1)),\dots,j"(iB(f_n)) ]\ge 3n+5. \end{align*} $$
As
![]() $f_1,f_2$
are the real and imaginary parts of
$f_1,f_2$
are the real and imaginary parts of
![]() $j(i+t)$
and the function B is algebraic and
$j(i+t)$
and the function B is algebraic and
![]() $i+t$
and
$i+t$
and
![]() $iB(t)$
are algebraically dependent we have that
$iB(t)$
are algebraically dependent we have that
 $$ \begin{align*}\text{tr.deg}_{\mathbb{C}}\mathbb{C}[&i+t,iB(t),iB(f_1),\dots,iB(f_n),\\&j(i+t),j(iB(t)),j(iB(f_1)),\dots, j(iB(f_n)), \\&j'(iB(t)),j'(iB(f_1)),\dots,j'(iB(f_n)),\\&j"(iB(t)), j"(iB(f_1)),\dots,j"(iB(f_n)) ]\le 3n+4, \end{align*} $$
$$ \begin{align*}\text{tr.deg}_{\mathbb{C}}\mathbb{C}[&i+t,iB(t),iB(f_1),\dots,iB(f_n),\\&j(i+t),j(iB(t)),j(iB(f_1)),\dots, j(iB(f_n)), \\&j'(iB(t)),j'(iB(f_1)),\dots,j'(iB(f_n)),\\&j"(iB(t)), j"(iB(f_1)),\dots,j"(iB(f_n)) ]\le 3n+4, \end{align*} $$
a contradiction.
6 Final remarks
It is reasonable to expect that further nondefinability results for transcendental functions such as the modular j-function can be obtained by adapting the methods given here. In particular an analogue of Theorem 1.1 for the modular j-function is a natural statement. However there are some obstructions in directly applying the method of Section 4 to this case. Firstly the necessity for a system of algebraic functions requires a reworking of the final part of the proof of Theorem 1.1 for such a system. Also the lack of addition formula for the modular j-function makes a direct application of the proof of Lemma 4.2 impossible.
However for the Weierstrass
![]() $\zeta $
-function, a quasi-periodic meromorphic function related to
$\zeta $
-function, a quasi-periodic meromorphic function related to
![]() $\wp $
by the formula
$\wp $
by the formula
![]() $\zeta '=\wp $
some definability results can be readily obtained. By using classical formulae and an Ax-Schanuel statement involving
$\zeta '=\wp $
some definability results can be readily obtained. By using classical formulae and an Ax-Schanuel statement involving
![]() $\wp $
and
$\wp $
and
![]() $\zeta $
, which is also due to Brownawell and Kubota in [Reference Brownawell and Kubota4] one can characterise the definability of restrictions of
$\zeta $
, which is also due to Brownawell and Kubota in [Reference Brownawell and Kubota4] one can characterise the definability of restrictions of
![]() $\zeta $
to a disc
$\zeta $
to a disc
![]() $D\subseteq \mathbb {C}$
in the structure
$D\subseteq \mathbb {C}$
in the structure
![]() $(\overline {\mathbb {R}},\wp |_I,\zeta |_I)$
, where
$(\overline {\mathbb {R}},\wp |_I,\zeta |_I)$
, where
![]() $I\subseteq \mathbb {R}$
is a bounded closed interval such that
$I\subseteq \mathbb {R}$
is a bounded closed interval such that
![]() $I\cap \Omega =\varnothing $
, in terms of complex multiplication. This is an analogue of Theorem 5.2 for the Weierstrass
$I\cap \Omega =\varnothing $
, in terms of complex multiplication. This is an analogue of Theorem 5.2 for the Weierstrass
![]() $\zeta $
-function and the proof is simply another adaptation of the method seen in the proof of Theorem 5.3.
$\zeta $
-function and the proof is simply another adaptation of the method seen in the proof of Theorem 5.3.
Acknowledgements
The author is also is grateful to the Heilbronn Institute for Mathematical Research for support. The author thanks the anonymous referee for comments that improved the presentation of this paper.
Funding
This work formed part of the author’s PhD thesis, which was supported by an Engineering and Physical Sciences Research Council Doctoral Training Award.