Article contents
Noncharacterizability of the syntax set
Published online by Cambridge University Press: 12 March 2014
Extract
Craig showed in [3] that Beth's theorem fails for 2nd order logic. This is so since the syntax for 2nd order logic can be represented in the structure 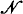 of natural numbers and
of natural numbers and 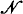 itself can be characterized in 2nd order logic. Thus the satisfaction relation S is implicitly definable yet not explicitly definable (by a Tarski diagonal argument) and Beth fails. Kreisel pointed out in a review of Craig's paper that a similar argument shows that Beth's theorem fails for ω-logic or for any logic whose syntax can be represented in
itself can be characterized in 2nd order logic. Thus the satisfaction relation S is implicitly definable yet not explicitly definable (by a Tarski diagonal argument) and Beth fails. Kreisel pointed out in a review of Craig's paper that a similar argument shows that Beth's theorem fails for ω-logic or for any logic whose syntax can be represented in 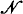 and in which
and in which 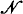 can be characterized. In this paper we use the abstract model-theoretic notions of truth adequacy, truth-maximality and truth-completeness developed by Feferman in [4] to prove the following generalization of Craig's result: If L is a truth-complete logic, then no structure in which the syntax is represented is L-characterizable. This is applied via a corollary to give new examples of failures of Beth's theorem. Another way to construe this result is that truth-complete logics L have the desirable model-theoretic property (see [5]) that the structure in which the syntax is represented is not generalized finite (interpreting generalized finite as L-characterizability).
can be characterized. In this paper we use the abstract model-theoretic notions of truth adequacy, truth-maximality and truth-completeness developed by Feferman in [4] to prove the following generalization of Craig's result: If L is a truth-complete logic, then no structure in which the syntax is represented is L-characterizable. This is applied via a corollary to give new examples of failures of Beth's theorem. Another way to construe this result is that truth-complete logics L have the desirable model-theoretic property (see [5]) that the structure in which the syntax is represented is not generalized finite (interpreting generalized finite as L-characterizability).
Since the basic notions of [4] are defined in terms of many-sorted logics, we will consider all our logics to be many-sorted.
- Type
- Research Article
- Information
- Copyright
- Copyright © Association for Symbolic Logic 1976
References
BIBLIOGRAPHY
- 2
- Cited by


