Hostname: page-component-586b7cd67f-2brh9 Total loading time: 0 Render date: 2024-11-23T06:10:19.997Z Has data issue: false hasContentIssue false
  • English
  • Français

Non-branching degrees in the Medvedev lattice of Π10 classes

Published online by Cambridge University Press:  12 March 2014

Christopher P. Alfeld
Christopher P. Alfeld*
Affiliation:
Department of Mathematics, University of Wisconsin, Madison, WI 53706, USA. E-mail: [email protected]
Get access Rights & Permissions [Opens in a new window]

Abstract

A 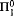class is the set of paths through a computable tree. Given classes P and Q, P is Medvedev reducible to Q, P ≤MQ, if there is a computably continuous functional mapping Q into P. We look at the lattice formed by 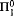subclasses of 2ω under this reduction. It is known that the degree of a splitting class of c.e. sets is non-branching. We further characterize non-branching degrees, providing two additional properties which guarantee non-branching: inseparable and hyperinseparable. Our main result is to show that non-branching iff inseparable if hyperinseparable if homogeneous and that all unstated implications do not hold. We also show that inseparable and not hyperinseparable degrees are downward dense.

Keywords

classesMedvedev latticenon-branching degree
Type
Research Article
Information
The Journal of Symbolic Logic , Volume 72 , Issue 1 , March 2007 , pp. 81 - 97
Copyright
Copyright © Association for Symbolic Logic 2007

Access options

Get access to the full version of this content by using one of the access options below. (Log in options will check for institutional or personal access. Content may require purchase if you do not have access.)

References

REFERENCES

[1]Binns, Stephen, A splitting theorem for the Medvedev and Muchnik lattices, Mathematical Logic Quarterly, vol. 49 (2003), no. 4, pp. 327–335.CrossRefGoogle Scholar
[2]Cenzer, Douglas and Hinman, Peter G., Density of the Medvedev lattice of classes, Archive for Mathematical Logic, vol. 42 (2003), no. 6, pp. 583–600.CrossRefGoogle Scholar
[3]Cenzer, Douglas and Jockusch, Carl G. Jr., classes—structure and applications, Computability theory and its applications (Boulder, CO, 1999), Contempory Mathematics, vol. 257, American Mathematics Society, Providence, RI, 2000, pp. 39–59.Google Scholar
[4]Cenzer, Douglas and Remmel, Jeffrey B., classes in mathematics, Handbook of recursive mathematics, vol. 2, Studies in Logic and the Foundations of Mathematics, vol. 139, North-Holland, Amsterdam, 1998, pp. 623–821.Google Scholar
[5]Rogers, Hartley Jr., Theory of recursive functions and effective computability, MIT Press, Cambridge, MA, 1987.Google Scholar
[6]Simpson, Stephen G., Mass problems and randomness, The Bulletin of Symbolic Logic, vol. 11 (2005), no. 1, pp. 1–27.CrossRefGoogle Scholar
[7]Simpson, Stephen G., sets and models of WKL0, Reverse mathematics 2001 (Simpson, S. G., editor), Lecture Notes in Logic, vol. 21, ASL and AK Peters, 2005, pp. 352–378.Google Scholar
[8]Soare, Robert I., Recursively enumerable sets and degrees, Perspectives in Mathematical Logic, Springer-Verlag, Berlin, 1987.CrossRefGoogle Scholar