Published online by Cambridge University Press: 12 March 2014
Craig's theorem is a result about the cardinality of a proper basis for the theory of combinators. Its proof given in [3] was shown to be incomplete by André Chauvin [2]. By using a different approach, we give a very short proof of this theorem. We use the notation of [1].
Definition 1. A combinator Q is proper if there exists a natural number n such that for arbitrary variables x1,…,xn we have the following contraction rule:
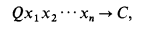
where C is a pure combination of the variables x1,…,xn. Q is to be understood as an abstract symbol, not as a combination of S and K's. Therefore Q comes with a contraction rule.
Definition 2. A set (Q1,…, Qm} of combinators is a basis for combinatory logic if for every finite set {x1,…, xk} of variables and every pure combination C of these variables, there exists a pure combination Q of Q1,…, Qm such that Qx1 … xk ↠ C.
Craig's Theorem. Every basis for combinatory logic containing only proper combinators contains at least two elements.
Proof. Let {Q} be a singleton basis for combinatory logic, and let us show that we cannot have combinatory completeness. This is an easy consequence of the next two lemmas.
Lemma 1. Q is a projection. That is, Qx1 … xn ↠ xj, for some j.
Proof. Let I be a proper combination of Q such that Ix ↠ x for a variable x, and let M be a term such that Ix ↠ M → x and M → x is a nontrivial contraction.