Hostname: page-component-cd9895bd7-dk4vv Total loading time: 0 Render date: 2025-01-03T11:51:19.936Z Has data issue: false hasContentIssue false
  • English
  • Français

Negative-existentially complete structures and definability in free extensions

Published online by Cambridge University Press:  12 March 2014

Volker Weispfenning
Volker Weispfenning*
Affiliation:
Universität Heidelberg, 6900 Heidelberg 1, West Germany
Get access Rights & Permissions [Opens in a new window]

Extract

Let R be a commutative ring with 1 and R[X 1, …, Xn ] the polynomial ring in n variables over R. Then for any relation f(X) = 0 in R[X] there exists a conjunction of equations φ f such that f(X) = 0 holds in R[X] iff φ f holds in R; φ f is of course the formula saying that all the coefficients of f(X) vanish. Moreover, φ f is independent of R and formed uniformly for all polynomials f up to a given formal degree. In this paper we investigate first order theories T for which a similar phenomenon holds. More precisely, we let TAH be the universal Horn part of a theory T and look at free extensions of models of T in the class of models of TAH . We ask whether an atomic relation t 1(X, a) = t 2(X, a) or R(t 1(X, a), …, tn (X, a)) in can be equivalently expressed by a finite or infinitary formula φ(a) in 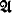, such that φ(y) depends only on t i{X, y) and not on 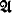or a 1, …, am ∈ A.

We will show that for a wide class of theories T “defining formulas” φ(y) in this sense exist and can be taken as infinite disjunctions of positive existential formulas.

Type
Research Article
Information
The Journal of Symbolic Logic , Volume 41 , Issue 1 , March 1976 , pp. 95 - 108
Copyright
Copyright © Association for Symbolic Logic 1976

Access options

Get access to the full version of this content by using one of the access options below. (Log in options will check for institutional or personal access. Content may require purchase if you do not have access.)

References

REFERENCES

[1] Amitsur, S. A., Polynomial identities and pivotal monomials, Transactions of the American Mathematical Society, vol. 114 (1965), pp. 210–226.CrossRefGoogle Scholar
[2] Cherlin, G., Algebraically closed commutative rings, this Journal, vol. 38 (1973), pp. 493–499.Google Scholar
[3] Cohn, P. M., The word problem for free fields, this Journal, vol. 38 (1973), pp. 309–314.Google Scholar
[4] Cohn, P. M., The word problem for free fields: a correction and addendum, this Journal, vol. 40 (1975), pp. 69–74.Google Scholar
[5] Eklof, P. and Sabbagh, G., Model-completions and modules, Annals of Mathematical Logic, vol. 2 (1971), pp. 251–295.CrossRefGoogle Scholar
[6] Hall, M., The theory of groups, Macmillan, New York, 1970.Google Scholar
[7] Lipshitz, L. and Saracino, D., The model-companion of the theory of commutative rings without nilpotent elements, Proceedings of the American Mathematical Society, vol. 38 (1973), pp. 381–387.CrossRefGoogle Scholar
[8] Robinson, A., A note on embedding problems, Fundamenta Mathematica, vol. 50 (1961/1962), pp. 455–461.CrossRefGoogle Scholar
[9] Robinson, A., A decision method for elementary algebra and geometry—revisited, Dedicated to Tarski, A., preprint, 10 1971.Google Scholar
[10] Wheeler, W., Algebraically closed division rings, forcing, and the analytic hierarchy, Doctoral Dissertation, Yale University, 1972.Google Scholar