Hostname: page-component-586b7cd67f-gb8f7 Total loading time: 0 Render date: 2024-11-26T23:10:29.911Z Has data issue: false hasContentIssue false
  • English
  • Français

Near-equational and equational systems of logic for partial functions. II1

Published online by Cambridge University Press:  12 March 2014

William Craig
William Craig*
Affiliation:
Department of Philosophy, University of California, Berkeley, California 94720
Get access Rights & Permissions [Opens in a new window]

Extract

For the reader's convenience, we begin Part II by restating the rules for constructing Sq derivations given in §2:

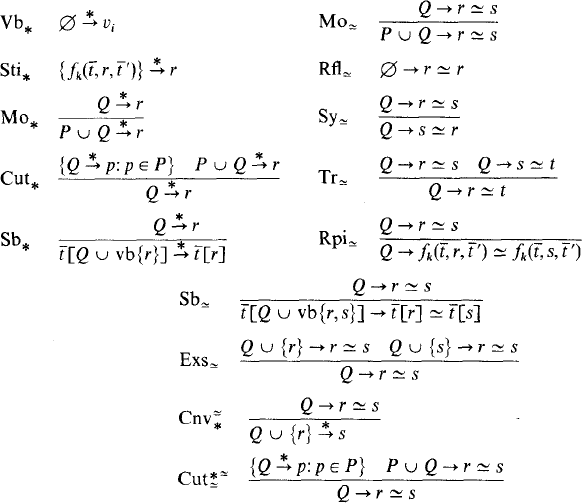
We let R be the set of 14 rules for Sq, R* the set of pure *-rules in R, R≃ the set of pure ≃-rules in R, and R− the set R ∩ − {Exs≃}. The closure of any F ⊆ Sq under R will be denoted by csR F, and the direct image of F under Cut*, for example, by Cut*(F).

Type
Research Article
Information
The Journal of Symbolic Logic , Volume 54 , Issue 4 , December 1989 , pp. 1181 - 1215
Copyright
Copyright © Association for Symbolic Logic 1989

Access options

Get access to the full version of this content by using one of the access options below. (Log in options will check for institutional or personal access. Content may require purchase if you do not have access.)

Footnotes

1

Part I, which consisted of §§ 1 – 3 and the bibliography, appeared in the previous issue of this Journal, pp. 795–827.

References

1 Part I, which consisted of §§ 1 – 3 and the bibliography, appeared in the previous issue of this Journal, pp. 795–827.