No CrossRef data available.
Published online by Cambridge University Press: 21 July 2020
For a given inner model N of ZFC, one can consider the relativized version of Berkeley cardinals in the context of ZFC, and ask if there can exist an “N-Berkeley cardinal.” In this article we provide a positive answer to this question. Indeed, under the assumption of a supercompact cardinal 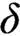 $\delta $
, we show that there exists a ZFC inner model N such that there is a cardinal which is N-Berkeley, even in a strong sense. Further, the involved model N is a weak extender model of
$\delta $
, we show that there exists a ZFC inner model N such that there is a cardinal which is N-Berkeley, even in a strong sense. Further, the involved model N is a weak extender model of 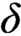 $\delta $
is supercompact. Finally, we prove that the strong version of N-Berkeley cardinals turns out to be inconsistent whenever N satisfies closure under
$\delta $
is supercompact. Finally, we prove that the strong version of N-Berkeley cardinals turns out to be inconsistent whenever N satisfies closure under 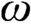 $\omega $
-sequences.
$\omega $
-sequences.