Published online by Cambridge University Press: 12 March 2014
In this paper we will present an application of generalized recursion theory to (noncombinatorial) set theory. More precisely we will combine a priority argument in α-recursion theory with a forcing construction to prove a theorem about the interdefinability of certain subsets of admissible ordinals.
Our investigation was prompted by G. Sacks and S. Simpson asking [6] if it is obvious that there are, for each Σn-admissible α, Σn (over L α ) subsets of α which are Δn -incomparable. If one understands “B is Δn in C” to mean that there are Σn /L α reduction procedures which put out B and 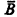 when one feeds in C, then the answer is an unqualified “yes.” In this sense “Δn in” is a direct generalization of “α-recursive in” (replace Σ1 by Σn in the definition) and so amenable to the methods of [7, §§3, 5]. Indeed one simply chooses a complete Σn−1 set A and mimics the construction of [6] as modified in [7, §5] to produce two α-A-r.e. sets B and C neither of which is α-A-recursive in the other. By the remarks on translation [7, §3] this will immediately give the desired result for this definition of “Δn in.”
when one feeds in C, then the answer is an unqualified “yes.” In this sense “Δn in” is a direct generalization of “α-recursive in” (replace Σ1 by Σn in the definition) and so amenable to the methods of [7, §§3, 5]. Indeed one simply chooses a complete Σn−1 set A and mimics the construction of [6] as modified in [7, §5] to produce two α-A-r.e. sets B and C neither of which is α-A-recursive in the other. By the remarks on translation [7, §3] this will immediately give the desired result for this definition of “Δn in.”
There is, however, the more obvious and natural notion of “Δn in” to be considered: B is Δn in C iff there are Σn and Πn formulas of ⟨L α , C⟩ which define B.
This paper consists of part of the author's Ph.D. Thesis, Massachusetts Institute of Technology, 1972, written under the direction of Professor G. E. Sacks. The author was partially supported by an NSF Graduate Fellowship.