Hostname: page-component-6bf8c574d5-7jkgd Total loading time: 0 Render date: 2025-02-16T16:39:32.546Z Has data issue: false hasContentIssue false
  • English
  • Français

MOST(?) THEORIES HAVE BOREL COMPLETE REDUCTS

Part of: Set theory Model theory

Published online by Cambridge University Press:  27 September 2021

MICHAEL C. LASKOWSKI  and
DOUGLAS S. ULRICH
MICHAEL C. LASKOWSKI*
Affiliation:
DEPARTMENT OF MATHEMATICS UNIVERSITY OF MARYLAND COLLEGE PARK, MD, USA E-mail: [email protected]
DOUGLAS S. ULRICH
Affiliation:
DEPARTMENT OF MATHEMATICS UNIVERSITY OF MARYLAND COLLEGE PARK, MD, USA E-mail: [email protected]
*
E-mail: [email protected]
Get access Rights & Permissions [Opens in a new window]

Abstract

We prove that many seemingly simple theories have Borel complete reducts. Specifically, if a countable theory has uncountably many complete one-types, then it has a Borel complete reduct. Similarly, if 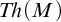$Th(M)$ is not small, then 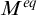$M^{eq}$ has a Borel complete reduct, and if a theory T is not 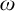$\omega $ -stable, then the elementary diagram of some countable model of T has a Borel complete reduct.

Keywords

Borel complexitycountable modelsreducts

MSC classification

Primary: 03C50: Models with special properties (saturated, rigid, etc.)
Secondary: 03E15: Descriptive set theory
Type
Article
Information
The Journal of Symbolic Logic , Volume 88 , Issue 1 , March 2023 , pp. 418 - 426
Check for updates
Copyright
© The Author(s), 2021. Published by Cambridge University Press on behalf of The Association for Symbolic Logic

Access options

Get access to the full version of this content by using one of the access options below. (Log in options will check for institutional or personal access. Content may require purchase if you do not have access.)

References

Friedman, H. and Stanley, L., A Borel reducibility theory for classes of countable structures, this Journal, vol. 54 (1989), no. 3, pp. 894–914.Google Scholar
Gao, S., Invariant Descriptive Set Theory, Chapman & Hall/CRC Pure and Applied Mathematics, vol. 293, CRC Press, Boca Raton, 2008.CrossRefGoogle Scholar
Kechris, A., Classical Descriptive Set Theory, Graduate Texts in Mathematics, vol. 156, Springer, New York, 1995.CrossRefGoogle Scholar
Laskowski, M. C., Mutually algebraic structures and expansions by predicates, this Journal, vol. 78 (2013), no. 1, pp. 185–194.Google Scholar
Laskowski, M. C. and Shelah, S., Borel complexity of some ${\aleph}_0$ -stable theories . Fundamenta Mathematicae, vol. 229 (2015), no. 1, pp. 1–46.CrossRefGoogle Scholar
Laskowski, M. C. and Ulrich, D. S., Characterizing the existence of a Borel complete expansion, submitted, arXiv:2109.06140.Google Scholar
Ulrich, D., Rast, R. and Laskowski, M. C., Borel complexity and potential canonical Scott sentences . Fundamenta Mathematicae, vol. 239 (2017), no. 2, pp. 101–147.CrossRefGoogle Scholar