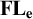Hostname: page-component-cd9895bd7-dzt6s Total loading time: 0 Render date: 2024-12-26T23:56:12.315Z Has data issue: false hasContentIssue false
  • English
  • Français

MOST SIMPLE EXTENSIONS OF $\textbf{FL}_{\textbf{e}}$ ARE UNDECIDABLE

Part of: General logic Varieties Ordered structures Algebraic logic

Published online by Cambridge University Press:  10 June 2021

NIKOLAOS GALATOS  and
GAVIN ST. JOHN
NIKOLAOS GALATOS
Affiliation:
DEPARTMENT OF MATHEMATICS UNIVERSITY OF DENVERDENVER, CO 80210, USAE-mail:[email protected]
GAVIN ST. JOHN
Affiliation:
DIPARTIMENTO DI PEDAGOGIA, PSICOLOGIA, & FILOSOFIA UNIVERSITÀ DI CAGLIARI09123CAGLIARI, ITALYE-mail:[email protected]
Get access Rights & Permissions [Opens in a new window]

Abstract

All known structural extensions of the substructural logic 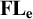$\textbf{FL}_{\textbf{e}}$ , the Full Lambek calculus with exchange/commutativity (corresponding to subvarieties of commutative residuated lattices axiomatized by 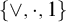$\{\vee , \cdot , 1\}$ -equations), have decidable theoremhood; in particular all the ones defined by knotted axioms enjoy strong decidability properties (such as the finite embeddability property). We provide infinitely many such extensions that have undecidable theoremhood, by encoding machines with undecidable halting problem. An even bigger class of extensions is shown to have undecidable deducibility problem (the corresponding varieties of residuated lattices have undecidable word problem); actually with very few exceptions, such as the knotted axioms and the other prespinal axioms, we prove that undecidability is ubiquitous. Known undecidability results for non-commutative extensions use an encoding that fails in the presence of commutativity, so and-branching counter machines are employed. Even these machines provide encodings that fail to capture proper extensions of commutativity, therefore we introduce a new variant that works on an exponential scale. The correctness of the encoding is established by employing the theory of residuated frames.

Keywords

substructural logicfull Lambek calculussimple extensionsresiduated latticeequational theoryword problemdecidability

MSC classification

Primary: 03B47: Substructural logics (including relevance, entailment, linear logic, Lambek calculus, BCK and BCI logics)
Secondary: 08B15: Lattices of varieties 03G10: Lattices and related structures 06F05: Ordered semigroups and monoids
Type
Article
Information
The Journal of Symbolic Logic , Volume 87 , Issue 3 , September 2022 , pp. 1156 - 1200
Check for updates
Copyright
© The Author(s), 2021. Published by Cambridge University Press on behalf of The Association for Symbolic Logic

Access options

Get access to the full version of this content by using one of the access options below. (Log in options will check for institutional or personal access. Content may require purchase if you do not have access.)

References

Blok, W. and Pigozzi, D., Algebraizable logics . Memoirs of the American Mathematical Society , vol. 77 (1989), no. 396, pp. 1–78.CrossRefGoogle Scholar
Cardona, R. and Galatos, N., The FEP for some varieties of fully distributive knotted residuated lattices . Algebra Universalis , vol. 78 (2017), no. 3, pp. 363–376.CrossRefGoogle Scholar
Chvalovský, K. and Horčík, R., Full lambek calculus with contraction is undecidable , this Journal, vol. 81 (2016), no. 2, pp. 524–540.Google Scholar
Ciabattoni, A., Galatos, N., and Terui, K., Algebraic proof theory for substructural logics: Cut-elimination and completions . Annals of Pure and Applied Logic , vol. 163 (2012), no. 3, pp. 266–290.CrossRefGoogle Scholar
Galatos, N. and Jipsen, P., Residuated frames with applications to decidability . Transactions of the American Mathematical Society , vol. 365 (2013), no. 3, pp. 1219–1249.CrossRefGoogle Scholar
Galatos, N., Jipsen, P., Kowalski, T., and Ono, H., Residuated Lattices: An Algebraic Glimpse at Substructural Logics , Studies in Logic and the Foundations of Mathematics, vol. 151, Elsevier, Amsterdam, 2007.Google Scholar
Hart, J., Rafter, L., and Tsinakis, C., The structure of commutative residuated lattices . International Journal of Algebra and Computation , vol. 12 (2002), pp. 509–524.CrossRefGoogle Scholar
Horčík, R., Word problem for knotted residuated lattices . Journal of Pure Applied Algebra , vol. 219 (2015), pp. 1548–1563.CrossRefGoogle Scholar
Jipsen, P. and Tsinakis, C., A survey of residuated lattices , Ordered Algebraic Structures (J. Martinez, editor), Developmental Mathematics, vol. 7, Kluwer Academic Publishers, Dordrecht, 2002, pp. 19–56.CrossRefGoogle Scholar
Lambek, J., How to program an infinite abacus . Canadian Mathematical Bulletin , vol. 4 (1961), pp. 265–302.CrossRefGoogle Scholar
Lincoln, P., Mitchell, J., Scedrov, A., and Shankar, N., Decision problems for propositional linear logic . Annals of Pure and Applied Logic , vol. 56 (1992), pp. 239–311.CrossRefGoogle Scholar
Lothaire, M., Algebraic Combinatorics on Words , Cambridge University Press, Cambridge, 2002.CrossRefGoogle Scholar
Minksy, M., Recursive unsolvability of Post's problem of ‘tag’ and other topics in the theory of Turing machines . The Annals of Mathematics , vol. 74 (1961), pp. 437–455.Google Scholar
Perng, C., On a class of theorems equivalent to Farkas's lemma . Applied Mathematical Sciences , vol. 11 (2017), no. 44, pp. 2175–2184.CrossRefGoogle Scholar
Roman, S., Positive Solutions to Linear Systems: Convexity and Separation , Springer, New York, 2005.Google Scholar
Urquhart, A., The complexity of decision procedures in relevance logic II , this Journal, vol. 64 (1999), no. 4, pp. 1774–1802.Google Scholar
van Alten, C. J., The finite model property for knotted extensions of propositional linear logic , this Journal, vol. 70 (2005), no. 1, pp. 84–98.Google Scholar