Article contents
MORE ON THE PRESERVATION OF LARGE CARDINALS UNDER CLASS FORCING
Published online by Cambridge University Press: 13 September 2021
Abstract
We prove two general results about the preservation of extendible and
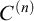 $C^{(n)}$
-extendible cardinals under a wide class of forcing iterations (Theorems 5.4 and 7.5). As applications we give new proofs of the preservation of Vopěnka’s Principle and
$C^{(n)}$
-extendible cardinals under a wide class of forcing iterations (Theorems 5.4 and 7.5). As applications we give new proofs of the preservation of Vopěnka’s Principle and
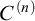 $C^{(n)}$
-extendible cardinals under Jensen’s iteration for forcing the GCH [17], previously obtained in [8, 27], respectively. We prove that
$C^{(n)}$
-extendible cardinals under Jensen’s iteration for forcing the GCH [17], previously obtained in [8, 27], respectively. We prove that
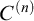 $C^{(n)}$
-extendible cardinals are preserved by forcing with standard Easton-support iterations for any possible
$C^{(n)}$
-extendible cardinals are preserved by forcing with standard Easton-support iterations for any possible
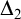 $\Delta _2$
-definable behaviour of the power-set function on regular cardinals. We show that one can force proper class-many disagreements between the universe and HOD with respect to the calculation of successors of regular cardinals, while preserving
$\Delta _2$
-definable behaviour of the power-set function on regular cardinals. We show that one can force proper class-many disagreements between the universe and HOD with respect to the calculation of successors of regular cardinals, while preserving
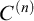 $C^{(n)}$
-extendible cardinals. We also show, assuming the GCH, that the class forcing iteration of Cummings–Foreman–Magidor for forcing
$C^{(n)}$
-extendible cardinals. We also show, assuming the GCH, that the class forcing iteration of Cummings–Foreman–Magidor for forcing
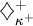 $\diamondsuit _{\kappa ^+}^+$
at every
$\diamondsuit _{\kappa ^+}^+$
at every
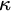 $\kappa $
[10] preserves
$\kappa $
[10] preserves
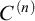 $C^{(n)}$
-extendible cardinals. We give an optimal result on the consistency of weak square principles and
$C^{(n)}$
-extendible cardinals. We give an optimal result on the consistency of weak square principles and
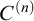 $C^{(n)}$
-extendible cardinals. In the last section prove another preservation result for
$C^{(n)}$
-extendible cardinals. In the last section prove another preservation result for
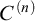 $C^{(n)}$
-extendible cardinals under very general (not necessarily definable or weakly homogeneous) class forcing iterations. As applications we prove the consistency of
$C^{(n)}$
-extendible cardinals under very general (not necessarily definable or weakly homogeneous) class forcing iterations. As applications we prove the consistency of
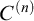 $C^{(n)}$
-extendible cardinals with
$C^{(n)}$
-extendible cardinals with
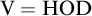 $\mathrm {{V}}=\mathrm {{HOD}}$
, and also with
$\mathrm {{V}}=\mathrm {{HOD}}$
, and also with
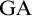 $\mathrm {GA}$
(the Ground Axiom) plus
$\mathrm {GA}$
(the Ground Axiom) plus
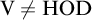 $\mathrm {V}\neq \mathrm {HOD}$
, the latter being a strengthening of a result from [14].
$\mathrm {V}\neq \mathrm {HOD}$
, the latter being a strengthening of a result from [14].
MSC classification
- Type
- Article
- Information
- Copyright
- © The Author(s), 2021. Published by Cambridge University Press on behalf of The Association for Symbolic Logic
References
- 1
- Cited by



