Hostname: page-component-cd9895bd7-gvvz8 Total loading time: 0 Render date: 2024-12-22T20:05:49.505Z Has data issue: false hasContentIssue false
  • English
  • Français

More on regular reduced products

Published online by Cambridge University Press:  12 March 2014

Juliette Cara Kennedy  and
Saharon Shelah
Juliette Cara Kennedy
Affiliation:
Department of Mathematics and Statistics, P.O. Box 68 (Gustaf Hällströmin Katu 2B), FI-00014, University of Helsinki, Finland, E-mail: [email protected]
Saharon Shelah
Affiliation:
Institute of Mathematics, Hebrew University, Jerusalem, Israel, E-mail: [email protected]
Get access Rights & Permissions [Opens in a new window]

Abstract.

The authors show, by means of a finitary version 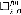of the combinatorial principle 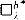of [7]. the consistency of the failure, relative to the consistency of supercompact cardinals, of the following: for all regular filters D on a cardinal λ. if Mi and Ni are elementarily equivalent models of a language of size ≤ λ, then the second player has a winning strategy in the Ehrenfeucht-Fraïssé game of length λ+ on ΠiMi/D and ΠiNi/D. If in addition 2λ = λ+ and i < λ implies |Mi| + |Ni| ≤ λ+ this means that the ultrapowers are isomorphic. This settles negatively conjecture 18 in [2].

Type
Research Article
Information
The Journal of Symbolic Logic , Volume 69 , Issue 4 , December 2004 , pp. 1261 - 1266
Copyright
Copyright © Association for Symbolic Logic 2004

Access options

Get access to the full version of this content by using one of the access options below. (Log in options will check for institutional or personal access. Content may require purchase if you do not have access.)

References

REFERENCES

[1]Ben-David, S., On Shelah's compactness of cardinals, Israel Journal of Mathematics, vol. 31 (1978), pp. 34–56.CrossRefGoogle Scholar
[2]Chang, C. C. and Keisler, J., Model theory, North-Holland, 1990.Google Scholar
[3]Keisler, J., Ultraproducts and saturated models, Koninklijke Nederlandse Akademie van Wetenschappen, Proceedings Series A, vol. 67 (1964), pp. 178–186, (= Indagationes Mathematicae. New Series, vol. 26).Google Scholar
[4]Kennedy, J. and Shelah, S., On regular reduced products, this Journal, vol. 67 (2002), pp. 1169–1177.Google Scholar
[5]Kennedy, J. and Shelah, S., On embedding models of arithmetic of cardinality ℵ1 into reduced powers, Fundamenta Mathematicae, vol. 176 (2003), no. 1, pp. 17–24.CrossRefGoogle Scholar
[6]Shelah, S., Every two elementarily equivalent models have isomorphic ultrapowers, Israel Journal of Mathematics, vol. 10 (1971), pp. 224–233.CrossRefGoogle Scholar
[7]Shelah, S., “Gap 1” two-cardinal principles and the omitting types theorem for L(Q), Israel Journal of Mathematics, vol. 65 (1989), no. 2, pp. 133–152.CrossRefGoogle Scholar