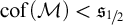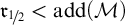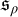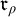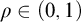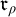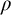1 Introduction
Let us recall the classical splitting number: Given
![]() $S, R\in [\omega ]^{\omega }$
we say that S splits R, in notation
$S, R\in [\omega ]^{\omega }$
we say that S splits R, in notation
![]() $S\mid R$
, if
$S\mid R$
, if
![]() $|S\cap R|=|R\smallsetminus S|=\omega $
; and the splitting number is defined as
$|S\cap R|=|R\smallsetminus S|=\omega $
; and the splitting number is defined as
In [Reference Bartoszyński and Judah4], among many other new cardinal invariants, the following variant of
![]() $\mathfrak {s}$
was introduced: For
$\mathfrak {s}$
was introduced: For
![]() $S,R\in [\omega ]^{\omega }$
we say that S bisects R, written as
$S,R\in [\omega ]^{\omega }$
we say that S bisects R, written as
, if
 $$ \begin{align*} \frac{|S\cap R\cap n|}{|R\cap n|}\xrightarrow{n\to\infty}\frac{1}{2}\text{,} \end{align*} $$
$$ \begin{align*} \frac{|S\cap R\cap n|}{|R\cap n|}\xrightarrow{n\to\infty}\frac{1}{2}\text{,} \end{align*} $$
and
is defined by replacing
![]() $\mid $
with
$\mid $
with
in the definition of
![]() $\mathfrak {s}$
,
$\mathfrak {s}$
,
As
implies
![]() $S \mid R$
,
$S \mid R$
,
immediately follows. It also turned out that
, where
![]() $\mathrm {cov}(\mathcal {M})$
stands for the covering number of the meagre ideal and
$\mathrm {cov}(\mathcal {M})$
stands for the covering number of the meagre ideal and
![]() $\mathrm {non}(\mathcal {N})$
for the uniformity of the null ideal (see below). Moreover, two of these inequalities are consistently strict (see [Reference Bartoszyński and Judah4, end of Section 2]):
$\mathrm {non}(\mathcal {N})$
for the uniformity of the null ideal (see below). Moreover, two of these inequalities are consistently strict (see [Reference Bartoszyński and Judah4, end of Section 2]):
in the Cohen model and
in the Mathias model. One of the most interesting remaining open questions is the following:
Question A. Is
![]() consistent?
consistent?
Of course, similar questions were raised regarding separations of
![]() and other classical invariants. For example (see [Reference Bartoszyński and Judah4, Question A (Q2)]), motivated by the fact that
and other classical invariants. For example (see [Reference Bartoszyński and Judah4, Question A (Q2)]), motivated by the fact that
![]() $\mathfrak {s}\leq \mathfrak {d}$
, where
$\mathfrak {s}\leq \mathfrak {d}$
, where
![]() $\mathfrak {d}$
stands for the dominating number (see below), it is natural to ask the following:
$\mathfrak {d}$
stands for the dominating number (see below), it is natural to ask the following:
Question B. Is
![]() consistent?
consistent?
In Section 2, we present a short overview on the relevant cardinal invariants (from [Reference Bartoszyński and Judah4]) and recall the inequalities and consistently strict inequalities between variants of
![]() $\mathfrak {s}$
and other classical cardinal characteristics.
$\mathfrak {s}$
and other classical cardinal characteristics.
In Section 3, by dualising the results from Section 2, we outline the inequalities between the variants of the reaping number
![]() $\mathfrak {r}$
and show the consistency of almost all possible strict inequalities in the dual diagram.
$\mathfrak {r}$
and show the consistency of almost all possible strict inequalities in the dual diagram.
In Section 4, answering Question B positively, we present two models of
![]() : (1) the
: (1) the
![]() $\omega _2$
-stage countable support iteration of a modified infinitely equal forcing and (2) the dual Hechler model, that is, the
$\omega _2$
-stage countable support iteration of a modified infinitely equal forcing and (2) the dual Hechler model, that is, the
![]() $\omega _1$
-stage finite support iteration of the Hechler forcing over a model of
$\omega _1$
-stage finite support iteration of the Hechler forcing over a model of
![]() .
.
In Section 5, we define natural generalisations of
![]() and
and
![]() , namely
, namely
![]() $\mathfrak {s}_{\rho }$
and
$\mathfrak {s}_{\rho }$
and
![]() $\mathfrak {r}_{\rho }$
for
$\mathfrak {r}_{\rho }$
for
![]() $\rho \in (0,1)$
. We discuss their lower and upper bounds and show that
$\rho \in (0,1)$
. We discuss their lower and upper bounds and show that
![]() $\mathfrak {r}_{\rho }$
does not depend on
$\mathfrak {r}_{\rho }$
does not depend on
![]() $\rho $
.
$\rho $
.
2 Variants of
 $\mathfrak {s}$
and
$\mathfrak {s}$
and
 $\mathfrak {r}$
$\mathfrak {r}$
When studying cardinal characteristics the following framework can come handy, especially when dualising inequalities and in the context of forcing. For a general overview on this framework, see, e.g., [Reference Blass and Shelah2] or [Reference Fremlin5, Section 512]. (Here, we mostly follow the notation of the second reference.)
Definition 2.1. A relational system is a triplet
![]() $\mathbf {R}=( X, \sqsubset , Y)$
where (i)
$\mathbf {R}=( X, \sqsubset , Y)$
where (i)
![]() $\sqsubset $
is a relation on
$\sqsubset $
is a relation on
![]() $X\times Y$
, (ii)
$X\times Y$
, (ii)
![]() $\mathrm {dom}(\sqsubset )=X$
, and (iii) there is no single
$\mathrm {dom}(\sqsubset )=X$
, and (iii) there is no single
![]() $y\in Y$
such that
$y\in Y$
such that
![]() $x\sqsubset y$
for every
$x\sqsubset y$
for every
![]() $x\in X$
.
$x\in X$
.
A set
![]() $U\subseteq X$
is
$U\subseteq X$
is
![]() $\mathbf {R}$
-unbounded if there is no single
$\mathbf {R}$
-unbounded if there is no single
![]() $y\in Y \ \sqsubset $
-above all elements of U; a set
$y\in Y \ \sqsubset $
-above all elements of U; a set
![]() $D\subseteq Y$
is
$D\subseteq Y$
is
![]() $\mathbf {R}$
-dominating if for every
$\mathbf {R}$
-dominating if for every
![]() $x\in X$
, there is a
$x\in X$
, there is a
![]() $y\in D \ \sqsubset $
-above x. The
$y\in D \ \sqsubset $
-above x. The
![]() $(un)$
bounding and dominating numbers of
$(un)$
bounding and dominating numbers of
![]() $\mathbf {R}$
are
$\mathbf {R}$
are
 $$ \begin{align*} \mathfrak{b}(\mathbf{R})=\mathfrak{b}(\sqsubset)&= \min\left\{|U| \;\middle|\; U \subseteq X\text{ is }\mathbf{R}\text{-unbounded}\right\}\!\text{,} \\ \mathfrak{d}(\mathbf{R})=\mathfrak{d}(\sqsubset)&= \min\left\{|D| \;\middle|\; D \subseteq Y\text{ is }\mathbf{R}\text{-dominating}\right\}\!\text{.} \end{align*} $$
$$ \begin{align*} \mathfrak{b}(\mathbf{R})=\mathfrak{b}(\sqsubset)&= \min\left\{|U| \;\middle|\; U \subseteq X\text{ is }\mathbf{R}\text{-unbounded}\right\}\!\text{,} \\ \mathfrak{d}(\mathbf{R})=\mathfrak{d}(\sqsubset)&= \min\left\{|D| \;\middle|\; D \subseteq Y\text{ is }\mathbf{R}\text{-dominating}\right\}\!\text{.} \end{align*} $$
The dual of
![]() $\mathbf {R}$
is the relational system
$\mathbf {R}$
is the relational system
![]() $\mathbf {R}^{\perp }=( Y, \not \sqsupset , X)$
(which satisfies conditions (i)–(iii) automatically). Clearly,
$\mathbf {R}^{\perp }=( Y, \not \sqsupset , X)$
(which satisfies conditions (i)–(iii) automatically). Clearly,
![]() $\mathfrak {b}(\mathbf {R}^{\perp })=\mathfrak {d}(\mathbf {R})$
and
$\mathfrak {b}(\mathbf {R}^{\perp })=\mathfrak {d}(\mathbf {R})$
and
![]() $\mathfrak {d}(\mathbf {R}^{\perp })=\mathfrak {b}(\mathbf {R})$
.
$\mathfrak {d}(\mathbf {R}^{\perp })=\mathfrak {b}(\mathbf {R})$
.
Example 2.2. We recall all relational systems and cardinal characteristics we need in the first four sections:
-
(1) Let
 $\mathbf {Dom}=(\omega ^{\omega },\leq ^*,\omega ^{\omega })$
, where
$\mathbf {Dom}=(\omega ^{\omega },\leq ^*,\omega ^{\omega })$
, where
 $f\leq ^* g$
if
$f\leq ^* g$
if
 $\{n \mid g(n)<f(n)\}$
is finite. Then
$\{n \mid g(n)<f(n)\}$
is finite. Then
 $\mathfrak {b}=\mathfrak {b}(\mathbf {Dom})$
and
$\mathfrak {b}=\mathfrak {b}(\mathbf {Dom})$
and
 $\mathfrak {d}=\mathfrak {d}(\mathbf {Dom})$
.
$\mathfrak {d}=\mathfrak {d}(\mathbf {Dom})$
. -
(2) Let
 $\mathcal {I}$
be an ideal on an infinite set X, that is,
$\mathcal {I}$
be an ideal on an infinite set X, that is,
 $[X]^{<\omega }\subseteq \mathcal {I}$
and
$[X]^{<\omega }\subseteq \mathcal {I}$
and
 $C\in \mathcal {I}$
whenever
$C\in \mathcal {I}$
whenever
 $C\subseteq A\cup B$
for some
$C\subseteq A\cup B$
for some
 $A,B \in \mathcal {I}$
; we will always assume that
$A,B \in \mathcal {I}$
; we will always assume that
 $X\notin \mathcal {I}$
. Consider the relational systems
$X\notin \mathcal {I}$
. Consider the relational systems
 $\mathbf {Cof}(\mathcal {I})=(\mathcal {I}, \subseteq , \mathcal {I})$
and
$\mathbf {Cof}(\mathcal {I})=(\mathcal {I}, \subseteq , \mathcal {I})$
and
 $\mathbf {Cov}(\mathcal {I})=(X,\in , \mathcal {I})$
. The four classical cardinal invariants of
$\mathbf {Cov}(\mathcal {I})=(X,\in , \mathcal {I})$
. The four classical cardinal invariants of
 $\mathcal {I}$
are the following cardinals: We know that
$\mathcal {I}$
are the following cardinals: We know that $$ \begin{align*} \mathrm{add}(\mathcal{I})&=\mathfrak{b}(\mathbf{Cof}(\mathcal{I}))\text{,} &\mathrm{cof}(\mathcal{I})&=\mathfrak{d}(\mathbf{Cof}(\mathcal{I}))\text{,}\\ \mathrm{non}(\mathcal{I})&=\mathfrak{b}(\mathbf{Cov}(\mathcal{I}))\text{,} &\mathrm{cov}(\mathcal{I})&=\mathfrak{d}(\mathbf{Cov}(\mathcal{I}))\text{.} \end{align*} $$
$$ \begin{align*} \mathrm{add}(\mathcal{I})&=\mathfrak{b}(\mathbf{Cof}(\mathcal{I}))\text{,} &\mathrm{cof}(\mathcal{I})&=\mathfrak{d}(\mathbf{Cof}(\mathcal{I}))\text{,}\\ \mathrm{non}(\mathcal{I})&=\mathfrak{b}(\mathbf{Cov}(\mathcal{I}))\text{,} &\mathrm{cov}(\mathcal{I})&=\mathfrak{d}(\mathbf{Cov}(\mathcal{I}))\text{.} \end{align*} $$
 $\mathrm {add}(\mathcal {I})\leq \mathrm {cov}(\mathcal {I}),\mathrm {non}(\mathcal {I})\leq \mathrm {cof}(\mathcal {I})$
always holds. We are particularly interested in two specific ideals, namely
$\mathrm {add}(\mathcal {I})\leq \mathrm {cov}(\mathcal {I}),\mathrm {non}(\mathcal {I})\leq \mathrm {cof}(\mathcal {I})$
always holds. We are particularly interested in two specific ideals, namely
 $\mathcal {M}=\{$
meagre subsets of
$\mathcal {M}=\{$
meagre subsets of
 $2^{\omega }\}$
and
$2^{\omega }\}$
and
 $\mathcal {N}=\{$
null subsets of
$\mathcal {N}=\{$
null subsets of
 $2^{\omega }\}$
. The well-known Cichoń’s diagram can be summarised in the following Tukey connections (see below):
$2^{\omega }\}$
. The well-known Cichoń’s diagram can be summarised in the following Tukey connections (see below):
 $\mathbf {Cov}(\mathcal {M})\preceq \mathbf {Dom}\preceq \mathbf {Cof}(\mathcal {M})\preceq \mathbf {Cof}(\mathcal {N})$
and
$\mathbf {Cov}(\mathcal {M})\preceq \mathbf {Dom}\preceq \mathbf {Cof}(\mathcal {M})\preceq \mathbf {Cof}(\mathcal {N})$
and
 $\mathbf {Cov}(\mathcal {N})\preceq \mathbf {Cov}(\mathcal {M})^{\perp }$
(and the facts that
$\mathbf {Cov}(\mathcal {N})\preceq \mathbf {Cov}(\mathcal {M})^{\perp }$
(and the facts that
 $\mathrm {add}(\mathcal {M})=\min \{\mathfrak {b},\mathrm {cov}(\mathcal {M})\}$
and
$\mathrm {add}(\mathcal {M})=\min \{\mathfrak {b},\mathrm {cov}(\mathcal {M})\}$
and
 $\mathrm {cof}(\mathcal {M})=\max \{\mathrm {non}(\mathcal {M}),\mathfrak {d}\}$
).
$\mathrm {cof}(\mathcal {M})=\max \{\mathrm {non}(\mathcal {M}),\mathfrak {d}\}$
).
-
(3) Let
 where
where
 $S \mid X$
(“S splits X”) if
$S \mid X$
(“S splits X”) if
 $|S \cap X|=|X \smallsetminus S|=\omega $
. Then
$|S \cap X|=|X \smallsetminus S|=\omega $
. Then
 $\mathfrak {s}=\mathfrak {b}(\mathbf {Reap})$
and
$\mathfrak {s}=\mathfrak {b}(\mathbf {Reap})$
and
 $\mathfrak {r}=\mathfrak {d}(\mathbf {Reap})$
.
$\mathfrak {r}=\mathfrak {d}(\mathbf {Reap})$
. -
(4) Let
 , where
, where
 (“S bisects X”) if Then
(“S bisects X”) if Then $$ \begin{align*} \frac{|S \cap X \cap n|}{|X \cap n|}\xrightarrow{n\to\infty} \frac{1}{2}\text{.} \end{align*} $$
$$ \begin{align*} \frac{|S \cap X \cap n|}{|X \cap n|}\xrightarrow{n\to\infty} \frac{1}{2}\text{.} \end{align*} $$
 and
and
 .
.
-
(5) For
 let
let
 , where
, where
 (“
(“
 $S \ \varepsilon $
-almost bisects X”) if for all but finitely many n Then
$S \ \varepsilon $
-almost bisects X”) if for all but finitely many n Then $$ \begin{align*} \frac{1}{2}-\varepsilon<\frac{|S \cap X \cap n|}{|X \cap n|}<\frac{1}{2}+\varepsilon\text{.} \end{align*} $$
$$ \begin{align*} \frac{1}{2}-\varepsilon<\frac{|S \cap X \cap n|}{|X \cap n|}<\frac{1}{2}+\varepsilon\text{.} \end{align*} $$
 and
and
 .
.
Unfortunately, it is still unclear whether
![]() depends on
depends on
![]() $\varepsilon $
(see [Reference Bartoszyński and Judah4, Question A (Q3)]). Whenever we claim anything about
$\varepsilon $
(see [Reference Bartoszyński and Judah4, Question A (Q3)]). Whenever we claim anything about
![]() or its invariants, we mean that our claim holds for every
or its invariants, we mean that our claim holds for every
![]() .
.
Theorem 2.3 (see [Reference Bartoszyński and Judah4, Theorem 2.4]).
The following relations hold, where
![]() $a\longrightarrow b$
means “
$a\longrightarrow b$
means “
![]() $a\leq b$
, consistently
$a\leq b$
, consistently
![]() $a<b$
” and
$a<b$
” and
![]() $a \dashrightarrow b$
means “
$a \dashrightarrow b$
means “
![]() $a \leq b$
, possibly
$a \leq b$
, possibly
![]() $a=b$
”:
$a=b$
”:

Regarding further inequalities between these cardinals (apart from separating
![]() from
from
![]() and/or
and/or
![]() $\mathrm {non}(\mathcal {N})$
), there was only one question left open, namely, if
$\mathrm {non}(\mathcal {N})$
), there was only one question left open, namely, if
![]() or
or
![]() hold. To show that this inequality does not hold, in Section 4 we will present a construction based on countable support iteration as well as one based on finite support iteration.
hold. To show that this inequality does not hold, in Section 4 we will present a construction based on countable support iteration as well as one based on finite support iteration.
3 The dual diagram
Although in the proof of Theorem 2.3 it was not stated explicitly, all inequalities were proved (or could have easily been proved) via Tukey connections.
Definition 3.1. Let
![]() $\mathbf {R}_0=(X_0,\sqsubset _0,Y_0)$
and
$\mathbf {R}_0=(X_0,\sqsubset _0,Y_0)$
and
![]() $\mathbf {R}_1=(X_1, \sqsubset _1, Y_1)$
be relational systems. A pair
$\mathbf {R}_1=(X_1, \sqsubset _1, Y_1)$
be relational systems. A pair
![]() $(F, G)$
of functions
$(F, G)$
of functions
![]() $F\colon X_0\to X_1$
and
$F\colon X_0\to X_1$
and
![]() $G\colon Y_1\to Y_0$
, in short
$G\colon Y_1\to Y_0$
, in short
![]() $(F,G)\colon \mathbf {R}_0\to \mathbf {R}_1$
, is a (Galois–)Tukey connection from
$(F,G)\colon \mathbf {R}_0\to \mathbf {R}_1$
, is a (Galois–)Tukey connection from
![]() $\mathbf {R}_0$
to
$\mathbf {R}_0$
to
![]() $\mathbf {R}_1$
if for any
$\mathbf {R}_1$
if for any
![]() $x_0 \in X_0$
and
$x_0 \in X_0$
and
![]() $y_1 \in Y_1$
,
$y_1 \in Y_1$
,
![]() $F(x_0) \sqsubset _1 y_1$
implies
$F(x_0) \sqsubset _1 y_1$
implies
![]() $x_0 \sqsubset _0 G(y_1)$
. This is commonly visualised as follows:
$x_0 \sqsubset _0 G(y_1)$
. This is commonly visualised as follows:

If there is a Tukey connection from
![]() $\mathbf {R}_0$
to
$\mathbf {R}_0$
to
![]() $\mathbf {R}_1$
, we say that
$\mathbf {R}_1$
, we say that
![]() $\mathbf {R}_0$
is Tukey-below
$\mathbf {R}_0$
is Tukey-below
![]() $\mathbf {R}_1$
and write
$\mathbf {R}_1$
and write
![]() $\mathbf {R}_0\preccurlyeq \mathbf {R}_1$
. Note that
$\mathbf {R}_0\preccurlyeq \mathbf {R}_1$
. Note that
![]() $(F,G)\colon \mathbf {R}_0\to \mathbf {R}_1$
is a Tukey connection iff
$(F,G)\colon \mathbf {R}_0\to \mathbf {R}_1$
is a Tukey connection iff
![]() $(G,F)\colon \mathbf {R}_1^{\perp }\to \mathbf {R}_0^{\perp }$
is a Tukey connection. We say that
$(G,F)\colon \mathbf {R}_1^{\perp }\to \mathbf {R}_0^{\perp }$
is a Tukey connection. We say that
![]() $\mathbf {R}_0$
and
$\mathbf {R}_0$
and
![]() $\mathbf {R}_1$
are Tukey-equivalent, denoted by
$\mathbf {R}_1$
are Tukey-equivalent, denoted by
![]() $\mathbf {R}_0 \equiv \mathbf {R}_1$
, when
$\mathbf {R}_0 \equiv \mathbf {R}_1$
, when
![]() $\mathbf {R}_0 \preccurlyeq \mathbf {R}_1$
and
$\mathbf {R}_0 \preccurlyeq \mathbf {R}_1$
and
![]() $\mathbf {R}_1 \preccurlyeq \mathbf {R}_0$
both hold.
$\mathbf {R}_1 \preccurlyeq \mathbf {R}_0$
both hold.
Recall that
![]() $\mathbf {R}_0 \preccurlyeq \mathbf {R}_1$
implies that
$\mathbf {R}_0 \preccurlyeq \mathbf {R}_1$
implies that
![]() $\mathfrak {b}(\mathbf {R}_0) \geq \mathfrak {b}(\mathbf {R}_1)$
and
$\mathfrak {b}(\mathbf {R}_0) \geq \mathfrak {b}(\mathbf {R}_1)$
and
![]() $\mathfrak {d}(\mathbf {R}_0) \leq \mathfrak {d}(\mathbf {R}_1)$
. For example, the proof of
$\mathfrak {d}(\mathbf {R}_0) \leq \mathfrak {d}(\mathbf {R}_1)$
. For example, the proof of
![]() in Theorem 2.3 actually shows
in Theorem 2.3 actually shows
![]() etc., and hence the dual inequalities (e.g.,
etc., and hence the dual inequalities (e.g.,
![]() ) hold as well.
) hold as well.
Let us point out that, after appropriate coding, all relational systems and Tukey connections we discuss in this paper are Borel in the following sense:
![]() $\mathbf {R}=(X,\sqsubset ,Y)$
is Borel if X and Y are Polish spaces and
$\mathbf {R}=(X,\sqsubset ,Y)$
is Borel if X and Y are Polish spaces and
![]() $\sqsubset $
is a Borel subset of
$\sqsubset $
is a Borel subset of
![]() $X\times Y$
; a Tukey reduction
$X\times Y$
; a Tukey reduction
![]() $(F,G)\colon (X_0,\sqsubset _0,Y_0)\to (X_1\sqsubset _1,Y_1)$
between Borel systems is Borel if both F and G are Borel functions. This can be particularly useful in the context of forcing: If
$(F,G)\colon (X_0,\sqsubset _0,Y_0)\to (X_1\sqsubset _1,Y_1)$
between Borel systems is Borel if both F and G are Borel functions. This can be particularly useful in the context of forcing: If
![]() $\mathbf {R}$
is Borel, then we say that a forcing notion
$\mathbf {R}$
is Borel, then we say that a forcing notion
![]() $\mathbb {P}$
is
$\mathbb {P}$
is
![]() $\mathbf {R}$
-dominating if
$\mathbf {R}$
-dominating if
It follows that if there is a Borel Tukey connection
![]() $\mathbf {R}_0\to \mathbf {R}_1$
and
$\mathbf {R}_0\to \mathbf {R}_1$
and
![]() $\mathbb {P}$
is
$\mathbb {P}$
is
![]() $\mathbf {R}_1$
-dominating, then
$\mathbf {R}_1$
-dominating, then
![]() $\mathbb {P}$
is
$\mathbb {P}$
is
![]() $\mathbf {R}_0$
-dominating as well. Instead of “
$\mathbf {R}_0$
-dominating as well. Instead of “
![]() $\mathbf {R}$
-dominating,” we will use the common more specific terms, e.g., “
$\mathbf {R}$
-dominating,” we will use the common more specific terms, e.g., “
![]() $\mathbb {P}$
adds a dominating real (over V)” means that
$\mathbb {P}$
adds a dominating real (over V)” means that
![]() $\mathbb {P}$
is
$\mathbb {P}$
is
![]() $\mathbf {Dom}$
-dominating, “
$\mathbf {Dom}$
-dominating, “
![]() $\mathbb {P}$
adds a random real” means that
$\mathbb {P}$
adds a random real” means that
![]() $\mathbb {P}$
is
$\mathbb {P}$
is
![]() $\mathbf {Cov}(\mathcal {N})^{\perp }$
-dominating, etc.; we can talk about adding splitting, bisecting or
$\mathbf {Cov}(\mathcal {N})^{\perp }$
-dominating, etc.; we can talk about adding splitting, bisecting or
![]() $\varepsilon $
-almost bisecting reals (over V) analogously.
$\varepsilon $
-almost bisecting reals (over V) analogously.
To dualise Theorem 2.3, we hence have to check the consistency of the strict inequalities. Before stating the dual form of Theorem 2.3, let us take a closer look at
![]() . The Borel reducibility
. The Borel reducibility
![]() (because
(because
![]() , see above) implies that if we add random reals, we also add bisecting reals over V. The next two lemmas illustrate that “too tame” forcing notions cannot increase
, see above) implies that if we add random reals, we also add bisecting reals over V. The next two lemmas illustrate that “too tame” forcing notions cannot increase
![]() . We assume that all forcing notions are atomless and separative; in particular, we assume that every condition p in a forcing notion
. We assume that all forcing notions are atomless and separative; in particular, we assume that every condition p in a forcing notion
![]() $\mathbb {P}$
has incompatible extensions.
$\mathbb {P}$
has incompatible extensions.
Lemma 3.2. If
![]() $\mathbb {P}$
is
$\mathbb {P}$
is
![]() $\sigma $
-centred, then it cannot add
$\sigma $
-centred, then it cannot add
![]() $\varepsilon $
-almost bisecting reals.
$\varepsilon $
-almost bisecting reals.
Proof Let
![]() $\mathbb {P} = \bigcup _{n\in \omega } C_n$
, where each
$\mathbb {P} = \bigcup _{n\in \omega } C_n$
, where each
![]() $C_n$
is centred, let
$C_n$
is centred, let
![]() $\dot {B}$
be a
$\dot {B}$
be a
![]() $\mathbb {P}$
-name for an element of
$\mathbb {P}$
-name for an element of
![]() $[\omega ]^{\omega }$
, and assume towards a contradiction that
$[\omega ]^{\omega }$
, and assume towards a contradiction that
for some
![]() $p\in \mathbb {P}$
and
$p\in \mathbb {P}$
and
![]() , that is,
, that is,
 $$ \begin{align*} p\Vdash \text{"}\frac{1}{2}-\varepsilon < \frac{|\dot{B}\cap X\cap n|}{|X\cap n|} < \frac{1}{2}+\varepsilon \text{ for almost all } n\text{"} \end{align*} $$
$$ \begin{align*} p\Vdash \text{"}\frac{1}{2}-\varepsilon < \frac{|\dot{B}\cap X\cap n|}{|X\cap n|} < \frac{1}{2}+\varepsilon \text{ for almost all } n\text{"} \end{align*} $$
for every
![]() $X\in [\omega ]^{\omega }\cap V$
. Fix an interval partition
$X\in [\omega ]^{\omega }\cap V$
. Fix an interval partition
![]() $(I_n)$
of
$(I_n)$
of
![]() $\omega $
such that
$\omega $
such that
![]() $|I_0|\geq 2$
and
$|I_0|\geq 2$
and
![]() $|I_n|> 2^{n}|I_{<n}|$
for every n (where
$|I_n|> 2^{n}|I_{<n}|$
for every n (where
![]() $I_{<n}=\bigcup _{k<n}I_k$
and
$I_{<n}=\bigcup _{k<n}I_k$
and
![]() $I_{<0}=\varnothing $
). First of all, we show that
$I_{<0}=\varnothing $
). First of all, we show that
 $$ \begin{align*} p\Vdash \text{"}\frac{1}{2}-\varepsilon' < \frac{|\dot{B}\cap I_n|}{|I_n|} < \frac{1}{2}+\varepsilon' \text{ for almost all } n\text{"} \end{align*} $$
$$ \begin{align*} p\Vdash \text{"}\frac{1}{2}-\varepsilon' < \frac{|\dot{B}\cap I_n|}{|I_n|} < \frac{1}{2}+\varepsilon' \text{ for almost all } n\text{"} \end{align*} $$
holds for every
![]() . To see this, fix such an
. To see this, fix such an
![]() $\varepsilon '$
; then, as
$\varepsilon '$
; then, as
![]() $p\Vdash $
“
$p\Vdash $
“
![]() $\dot {B} \ \varepsilon $
-almost bisects
$\dot {B} \ \varepsilon $
-almost bisects
![]() $\omega $
,” p forces that for every sufficiently large n,
$\omega $
,” p forces that for every sufficiently large n,
 $$ \begin{align*} \frac{|\dot{B}\cap I_n|}{|I_n|} &\leq \frac{(1+2^{-n})|\dot{B}\cap I_{\leq n}|}{ (1+2^{-n})|I_n|}< \frac{(1+2^{-n})|\dot{B}\cap I_{\leq n}|}{ |I_{\leq n}|} \\ &<(1+2^{-n})\left(\frac{1}{2}+\varepsilon\right)<\frac{1}{2}+\varepsilon'\text{,} \end{align*} $$
$$ \begin{align*} \frac{|\dot{B}\cap I_n|}{|I_n|} &\leq \frac{(1+2^{-n})|\dot{B}\cap I_{\leq n}|}{ (1+2^{-n})|I_n|}< \frac{(1+2^{-n})|\dot{B}\cap I_{\leq n}|}{ |I_{\leq n}|} \\ &<(1+2^{-n})\left(\frac{1}{2}+\varepsilon\right)<\frac{1}{2}+\varepsilon'\text{,} \end{align*} $$
where the second inequality follows from
![]() $|I_n|+2^{-n}|I_n|>|I_n|+|I_{<n}|$
. The lower bound can be established similarly: p forces that for every sufficiently large n,
$|I_n|+2^{-n}|I_n|>|I_n|+|I_{<n}|$
. The lower bound can be established similarly: p forces that for every sufficiently large n,
 $$ \begin{align*} \frac{|\dot{B}\cap I_n|}{|I_n|}> \frac{|\dot{B}\cap I_n|}{|I_n|}+\frac{|I_{<n}|}{|I_n|}-2^{-n}\geq\frac{|\dot{B}\cap I_{\leq n}|}{|I_{\leq n}|}-2^{-n}>\frac{1}{2}-\varepsilon-2^{-n}>\frac{1}{2}-\varepsilon'\text{.} \end{align*} $$
$$ \begin{align*} \frac{|\dot{B}\cap I_n|}{|I_n|}> \frac{|\dot{B}\cap I_n|}{|I_n|}+\frac{|I_{<n}|}{|I_n|}-2^{-n}\geq\frac{|\dot{B}\cap I_{\leq n}|}{|I_{\leq n}|}-2^{-n}>\frac{1}{2}-\varepsilon-2^{-n}>\frac{1}{2}-\varepsilon'\text{.} \end{align*} $$
Fix an
![]() $\varepsilon '$
as above. Then there is a
$\varepsilon '$
as above. Then there is a
![]() $p'\leq p$
and an
$p'\leq p$
and an
![]() $N\in \omega $
such that
$N\in \omega $
such that
 $$ \begin{align*} p'\Vdash\text{"}\frac{1}{2}-\varepsilon' < \frac{|\dot{B}\cap I_n|}{|I_n|} < \frac{1}{2}+\varepsilon'\text{ for every } n\geq N \text{."} \end{align*} $$
$$ \begin{align*} p'\Vdash\text{"}\frac{1}{2}-\varepsilon' < \frac{|\dot{B}\cap I_n|}{|I_n|} < \frac{1}{2}+\varepsilon'\text{ for every } n\geq N \text{."} \end{align*} $$
By modifying
![]() $\dot {B}$
on
$\dot {B}$
on
![]() $I_{<N}$
(which does not affect the property of being
$I_{<N}$
(which does not affect the property of being
![]() $\varepsilon $
-almost bisecting), we can assume that
$\varepsilon $
-almost bisecting), we can assume that
![]() $p'$
forces these inequalities for every n; in particular,
$p'$
forces these inequalities for every n; in particular,
![]() $\dot {B}\cap I_n\ne \varnothing $
for every n (as
$\dot {B}\cap I_n\ne \varnothing $
for every n (as
![]() $\varepsilon '$
can be very small, we assume that
$\varepsilon '$
can be very small, we assume that
![]() $|I_n|$
is even for every n). In the rest of the proof we assume that
$|I_n|$
is even for every n). In the rest of the proof we assume that
![]() $p'=1_{\mathbb {P}}$
, that is,
$p'=1_{\mathbb {P}}$
, that is,
 $$ \begin{align} \Vdash\text{"}\frac{1}{2}-\varepsilon' < \frac{|\dot{B}\cap I_n|}{|I_n|} < \frac{1}{2}+\varepsilon'\text{ for every } n\text{."} \end{align} $$
$$ \begin{align} \Vdash\text{"}\frac{1}{2}-\varepsilon' < \frac{|\dot{B}\cap I_n|}{|I_n|} < \frac{1}{2}+\varepsilon'\text{ for every } n\text{."} \end{align} $$
Let
![]() $\mathcal {E}_n=\{E\subseteq I_n \mid \forall \, p\in C_n\; \exists \, q\leq p\colon q\Vdash \dot {B}\cap I_n=E\}$
. Note that
$\mathcal {E}_n=\{E\subseteq I_n \mid \forall \, p\in C_n\; \exists \, q\leq p\colon q\Vdash \dot {B}\cap I_n=E\}$
. Note that
![]() $\mathcal {E}_n\neq \varnothing $
: Otherwise, for every
$\mathcal {E}_n\neq \varnothing $
: Otherwise, for every
![]() $E\subseteq I_n$
we can fix
$E\subseteq I_n$
we can fix
![]() $p_E\in C_n$
such that
$p_E\in C_n$
such that
![]() $p_E\Vdash \dot {B}\cap I_n\neq E$
, but these
$p_E\Vdash \dot {B}\cap I_n\neq E$
, but these
![]() $p_E$
have a common extension, which is a contradiction. Fix an arbitrary sequence
$p_E$
have a common extension, which is a contradiction. Fix an arbitrary sequence
![]() $(E_n)_{n \in \omega }\in V$
such that
$(E_n)_{n \in \omega }\in V$
such that
![]() $E_n\in \mathcal {E}_n$
for every n (we know that
$E_n\in \mathcal {E}_n$
for every n (we know that
![]() $E_n\ne \varnothing $
), and let
$E_n\ne \varnothing $
), and let
![]() $X=\bigcup _{n\in \omega }E_n\in [\omega ]^{\omega }\cap V$
.
$X=\bigcup _{n\in \omega }E_n\in [\omega ]^{\omega }\cap V$
.
Since
![]() $\dot {B} \ \varepsilon $
-almost bisects X, we can fix some
$\dot {B} \ \varepsilon $
-almost bisects X, we can fix some
![]() $p\in \mathbb {P}$
and
$p\in \mathbb {P}$
and
![]() $M \in \omega $
such that
$M \in \omega $
such that

Now fix a k such that

As each condition has incompatible extensions, there are extensions of p in infinitely many
![]() $C_n$
; hence for some
$C_n$
; hence for some
![]() $n \geq k$
, we can fix a
$n \geq k$
, we can fix a
![]() $p'\in C_n$
below p. By the definition of
$p'\in C_n$
below p. By the definition of
![]() $\mathcal {E}_n$
, there is a
$\mathcal {E}_n$
, there is a
![]() $q\leq p'$
which forces that
$q\leq p'$
which forces that
![]() $\dot {B}\cap I_n=E_n=X\cap I_n$
; in particular, q forces that
$\dot {B}\cap I_n=E_n=X\cap I_n$
; in particular, q forces that

where the second inequality follows from Equation (*1) and the third inequality follows from
![]() $|I_{<n}|<2^{-n}|I_n|$
. This contradicts Equation (*2), because
$|I_{<n}|<2^{-n}|I_n|$
. This contradicts Equation (*2), because
![]() $I_{\leq n}=\min (I_{n+1})\geq \min (I_{k+1})\geq M$
.
$I_{\leq n}=\min (I_{n+1})\geq \min (I_{k+1})\geq M$
.
Before the next lemma, let us recall the Laver property. A forcing notion
![]() $\mathbb {P}$
has the Laver property (see [Reference Blass1, Definition 6.3.27]) if for every sequence
$\mathbb {P}$
has the Laver property (see [Reference Blass1, Definition 6.3.27]) if for every sequence
![]() $(H_n)_{n\in \omega }$
of non-empty finite sets and every
$(H_n)_{n\in \omega }$
of non-empty finite sets and every
![]() $\mathbb {P}$
-name
$\mathbb {P}$
-name
![]() $\dot {f}\in \prod _{n\in \omega }H_n$
, there is an
$\dot {f}\in \prod _{n\in \omega }H_n$
, there is an
![]() $S\in \prod _{n\in \omega } [H_n]^{2^n}$
(in V) such that
$S\in \prod _{n\in \omega } [H_n]^{2^n}$
(in V) such that
![]() $\Vdash _{\mathbb {P}}$
“
$\Vdash _{\mathbb {P}}$
“
![]() $\dot {f}(n)\in S(n)$
for almost all n.”
$\dot {f}(n)\in S(n)$
for almost all n.”
Lemma 3.3. If
![]() $\mathbb {P}$
has the Laver property, then it cannot add
$\mathbb {P}$
has the Laver property, then it cannot add
![]() $\varepsilon $
-almost bisecting reals.
$\varepsilon $
-almost bisecting reals.
Proof Assume towards a contradiction that a
![]() $p\in \mathbb {P}$
forces that
$p\in \mathbb {P}$
forces that
![]() $\dot {B}\in V^{\mathbb {P}} \ \varepsilon $
-almost bisects every
$\dot {B}\in V^{\mathbb {P}} \ \varepsilon $
-almost bisects every
![]() $X\in [\omega ]^{\omega }\cap V$
. As in the proof of Lemma 3.2, we fix an interval partition
$X\in [\omega ]^{\omega }\cap V$
. As in the proof of Lemma 3.2, we fix an interval partition
![]() $(I_n)$
in V such that
$(I_n)$
in V such that
![]() $|I_0|\geq 2$
and
$|I_0|\geq 2$
and
![]() $|I_n|>2^n|I_{<n}|$
for every n as well as an
$|I_n|>2^n|I_{<n}|$
for every n as well as an
, and just like above, we can assume that
 $$ \begin{align} p\Vdash\text{"}\frac{1}{2}-\varepsilon' < \frac{|\dot{B}\cap I_n|}{|I_n|} < \frac{1}{2}+\varepsilon'\text{ for every } n \text{."} \end{align} $$
$$ \begin{align} p\Vdash\text{"}\frac{1}{2}-\varepsilon' < \frac{|\dot{B}\cap I_n|}{|I_n|} < \frac{1}{2}+\varepsilon'\text{ for every } n \text{."} \end{align} $$
Let
![]() $Q_0=I_1$
,
$Q_0=I_1$
,
![]() $Q_1=I_2\cup I_3$
, …,
$Q_1=I_2\cup I_3$
, …,
![]() $Q_m=\bigcup _{m'<2^m} I_{2^{m}+m'}$
be the union of the next
$Q_m=\bigcup _{m'<2^m} I_{2^{m}+m'}$
be the union of the next
![]() $2^m$
many intervals in the partition. Applying the Laver property, there are an
$2^m$
many intervals in the partition. Applying the Laver property, there are an
![]() $S\in \prod _{m\in \omega }[\mathcal {P}(Q_m)]^{2^m}$
in V,
$S\in \prod _{m\in \omega }[\mathcal {P}(Q_m)]^{2^m}$
in V,
![]() $S(m)=\{S^m_{m'} \mid m'<2^m\}$
, a
$S(m)=\{S^m_{m'} \mid m'<2^m\}$
, a
![]() $p' \leq p$
, and a
$p' \leq p$
, and a
![]() $\mathbb {P}$
-name
$\mathbb {P}$
-name
![]() $\dot {b}$
for an element of
$\dot {b}$
for an element of
![]() $\prod _{m\in \omega }2^m$
such that
$\prod _{m\in \omega }2^m$
such that
![]() $p'\Vdash $
“
$p'\Vdash $
“
![]() $\dot {B}\cap Q_m=S^m_{\dot {b}(m)}\in S(m)$
for every m.” Define
$\dot {B}\cap Q_m=S^m_{\dot {b}(m)}\in S(m)$
for every m.” Define
Then X is infinite because
![]() $X\cap I_{2^m+\dot {b}(m)}= S^m_{\dot {b}(m)}\cap I_{2^m+\dot {b}(m)}=\dot {B}\cap I_{2^m+\dot {b}(m)}\neq \varnothing $
for every m. We claim that
$X\cap I_{2^m+\dot {b}(m)}= S^m_{\dot {b}(m)}\cap I_{2^m+\dot {b}(m)}=\dot {B}\cap I_{2^m+\dot {b}(m)}\neq \varnothing $
for every m. We claim that
![]() $p'\Vdash $
“
$p'\Vdash $
“
![]() $\dot {B}$
does not
$\dot {B}$
does not
![]() $\varepsilon $
-almost bisect X.” To see this, let m be sufficiently large such that
$\varepsilon $
-almost bisect X.” To see this, let m be sufficiently large such that

Then
![]() $p'$
forces that
$p'$
forces that

where we used Equation (*3) in the second inequality and
![]() $|I_{<n}|/|I_n|<2^{-n}$
in the third one.
$|I_{<n}|/|I_n|<2^{-n}$
in the third one.
Theorem 3.4. The following relations hold, where
![]() $a\longrightarrow b$
means “
$a\longrightarrow b$
means “
![]() $a\leq b$
, consistently
$a\leq b$
, consistently
![]() $a<b$
” and
$a<b$
” and
![]() $a \dashrightarrow b$
means “
$a \dashrightarrow b$
means “
![]() $a \leq b$
, possibly
$a \leq b$
, possibly
![]() $a=b$
,” and there are no further provable inequalities between these cardinals:
$a=b$
,” and there are no further provable inequalities between these cardinals:

Proof The inequalities follow by dualising the ones in Theorem 2.3. To show the consistency of the strict inequalities and that there are no further inequalities in
![]() $\mathrm {ZFC}$
, keeping in mind the consistent cuts of the Cichoń’s diagram, it is enough to show that the following are consistent:
$\mathrm {ZFC}$
, keeping in mind the consistent cuts of the Cichoń’s diagram, it is enough to show that the following are consistent:
![]() $\mathfrak {r}<\mathrm {non}(\mathcal {M})$
and
$\mathfrak {r}<\mathrm {non}(\mathcal {M})$
and
![]() (separately, of course).
(separately, of course).
![]() $\mathfrak {r}<\mathrm {non}(\mathcal {M})$
holds in the model presented in [Reference Brendle, Halbeisen, Klausner, Lischka and Shelah3, Section 5], because it is a model of
$\mathfrak {r}<\mathrm {non}(\mathcal {M})$
holds in the model presented in [Reference Brendle, Halbeisen, Klausner, Lischka and Shelah3, Section 5], because it is a model of
![]() $\mathfrak {u}<\mathfrak {s}$
and we know that
$\mathfrak {u}<\mathfrak {s}$
and we know that
![]() $\mathfrak {r}\leq \mathfrak {u}$
and
$\mathfrak {r}\leq \mathfrak {u}$
and
![]() $\mathfrak {s}\leq \mathrm {non}(\mathcal {M})$
(for more details on the ultrafilter number
$\mathfrak {s}\leq \mathrm {non}(\mathcal {M})$
(for more details on the ultrafilter number
![]() $\mathfrak {u}$
, see [Reference Blass and Shelah2, Section 9]).
$\mathfrak {u}$
, see [Reference Blass and Shelah2, Section 9]).
We show that
![]() holds after the
holds after the
![]() $\mathfrak {c}^+$
stage finite support iteration
$\mathfrak {c}^+$
stage finite support iteration
![]() $\mathbb {D}_{\mathfrak {c}^+}$
of the Hechler forcing
$\mathbb {D}_{\mathfrak {c}^+}$
of the Hechler forcing
![]() $\mathbb {D}$
. We know that if
$\mathbb {D}$
. We know that if
![]() $\kappa \geq \mathfrak {c}$
is regular, then
$\kappa \geq \mathfrak {c}$
is regular, then
![]() $V^{\mathbb {D}_{\kappa }}\vDash \mathrm {add}(\mathcal {M})=\min \{\mathfrak {b},\mathrm {cov}(\mathcal {M})\}=\kappa =\mathfrak {c}$
because
$V^{\mathbb {D}_{\kappa }}\vDash \mathrm {add}(\mathcal {M})=\min \{\mathfrak {b},\mathrm {cov}(\mathcal {M})\}=\kappa =\mathfrak {c}$
because
![]() $\mathbb {D}$
adds both dominating and Cohen reals. Recall (folklore, see [Reference Goldstern and Judah7]) that if
$\mathbb {D}$
adds both dominating and Cohen reals. Recall (folklore, see [Reference Goldstern and Judah7]) that if
![]() $\delta \leq \mathfrak {c}$
(hence also if
$\delta \leq \mathfrak {c}$
(hence also if
![]() $\delta <\mathfrak {c}^+$
) and
$\delta <\mathfrak {c}^+$
) and
![]() $(\mathbb {P}_{\alpha },\dot {\mathbb {Q}}_{\beta })_{\alpha \leq \delta , \beta <\delta }$
is a finite support iteration of
$(\mathbb {P}_{\alpha },\dot {\mathbb {Q}}_{\beta })_{\alpha \leq \delta , \beta <\delta }$
is a finite support iteration of
![]() $\sigma $
-centred forcing notions (that is,
$\sigma $
-centred forcing notions (that is,
![]() $\Vdash _{\alpha }$
“
$\Vdash _{\alpha }$
“
![]() $\dot {\mathbb {Q}}_{\alpha }$
is
$\dot {\mathbb {Q}}_{\alpha }$
is
![]() $\sigma $
-centred” for every
$\sigma $
-centred” for every
![]() $\alpha <\delta $
), then
$\alpha <\delta $
), then
![]() $\mathbb {P}_{\delta }$
is also
$\mathbb {P}_{\delta }$
is also
![]() $\sigma $
-centred. Applying Lemma 3.2, it follows that if
$\sigma $
-centred. Applying Lemma 3.2, it follows that if
![]() $\delta \leq \mathfrak {c}^+$
and
$\delta \leq \mathfrak {c}^+$
and
![]() $(\mathbb {P}_{\alpha },\dot {\mathbb {Q}}_{\beta })_{\alpha \leq \delta ,\beta <\delta }$
is a finite support iteration of
$(\mathbb {P}_{\alpha },\dot {\mathbb {Q}}_{\beta })_{\alpha \leq \delta ,\beta <\delta }$
is a finite support iteration of
![]() $\sigma $
-centred forcing notions, then
$\sigma $
-centred forcing notions, then
in particular,
![]() .
.
Probably the most interesting remaining open question is the following:
Question C. Is
![]() consistent?
consistent?
4 Models of

Let us recall the infinitely equal forcing
![]() $\mathbb {EE}$
(see [Reference Blass1, Definition 7.4.11]):
$\mathbb {EE}$
(see [Reference Blass1, Definition 7.4.11]):
![]() $p\in \mathbb {EE}$
if p is a function,
$p\in \mathbb {EE}$
if p is a function,
![]() $\mathrm {dom}(p)\subseteq \omega $
is coinfinite, and
$\mathrm {dom}(p)\subseteq \omega $
is coinfinite, and
![]() $p(n)\colon n\to 2$
is a function for every n; if p and q are conditions,
$p(n)\colon n\to 2$
is a function for every n; if p and q are conditions,
![]() $q\leq p$
if
$q\leq p$
if
![]() $q\supseteq p$
. We know (see [Reference Blass1, Lemmas 7.4.12 and 7.4.14]) that
$q\supseteq p$
. We know (see [Reference Blass1, Lemmas 7.4.12 and 7.4.14]) that
![]() $\mathbb {EE}$
and its countable support iterations are proper and
$\mathbb {EE}$
and its countable support iterations are proper and
![]() $\omega ^{\omega }$
-bounding and preserve non-meagre sets (see also [Reference Blass1, Lemma 6.3.21 and Theorems 6.1.13 and 6.3.5]).
$\omega ^{\omega }$
-bounding and preserve non-meagre sets (see also [Reference Blass1, Lemma 6.3.21 and Theorems 6.1.13 and 6.3.5]).
We will work with a variant of
![]() $\mathbb {EE}$
. Basically, we do the following: (i) We allow longer characteristic functions in the n-th coordinate (but still below a common bound); and to adapt the forcing notion to our needs, (ii) we switch from characteristic functions to subsets and (iii) by shifting the underlying set in the n-th coordinate, we make sure that in the generic sequence, these finite sets are ordered consecutively.
$\mathbb {EE}$
. Basically, we do the following: (i) We allow longer characteristic functions in the n-th coordinate (but still below a common bound); and to adapt the forcing notion to our needs, (ii) we switch from characteristic functions to subsets and (iii) by shifting the underlying set in the n-th coordinate, we make sure that in the generic sequence, these finite sets are ordered consecutively.
More precisely, we fix an interval partition
![]() $(I_n)$
of
$(I_n)$
of
![]() $\omega $
as in Lemma 3.2 and Lemma 3.3, that is,
$\omega $
as in Lemma 3.2 and Lemma 3.3, that is,
![]() $|I_0|\geq 2$
and
$|I_0|\geq 2$
and
![]() $|I_n|>2^n|I_{<n}|$
for every n, and define
$|I_n|>2^n|I_{<n}|$
for every n, and define
![]() $\mathbb {P}=\mathbb {P}_{(I_n)}$
as follows:
$\mathbb {P}=\mathbb {P}_{(I_n)}$
as follows:
![]() $p\in \mathbb {P}$
if p is function such that:
$p\in \mathbb {P}$
if p is function such that:
-
(a)
 $\mathrm {dom}(p)\subseteq \omega $
is coinfinite and
$\mathrm {dom}(p)\subseteq \omega $
is coinfinite and -
(b)
 $p(n)\subseteq I_n$
for every
$p(n)\subseteq I_n$
for every
 $n\in \mathrm {dom}(p)$
;
$n\in \mathrm {dom}(p)$
;
![]() $q\leq p$
if
$q\leq p$
if
![]() $q\supseteq p$
. The very same proofs that work for
$q\supseteq p$
. The very same proofs that work for
![]() $\mathbb {EE}$
show that
$\mathbb {EE}$
show that
![]() $\mathbb {P}$
and its countable support iterations are proper and
$\mathbb {P}$
and its countable support iterations are proper and
![]() $\omega ^{\omega }$
-bounding and preserve non-meagre sets. It follows that if ch holds in the ground model, then
$\omega ^{\omega }$
-bounding and preserve non-meagre sets. It follows that if ch holds in the ground model, then
![]() $\mathbb {P}_{\omega _2}$
(the
$\mathbb {P}_{\omega _2}$
(the
![]() $\omega _2$
-stage countable support iteration of
$\omega _2$
-stage countable support iteration of
![]() $\mathbb {P}$
) forces that
$\mathbb {P}$
) forces that
![]() $\mathrm {cof}(\mathcal {M})=\max \{\mathrm {non}(\mathcal {M}),\mathfrak {d}\}=\omega _1$
.
$\mathrm {cof}(\mathcal {M})=\max \{\mathrm {non}(\mathcal {M}),\mathfrak {d}\}=\omega _1$
.
Lemma 4.1. Let
![]() $\dot {G}$
be the canonical
$\dot {G}$
be the canonical
![]() $\mathbb {P}$
-name of the
$\mathbb {P}$
-name of the
![]() $\mathbb {P}$
-generic filter and let
$\mathbb {P}$
-generic filter and let
![]() $\dot {X}$
be a
$\dot {X}$
be a
![]() $\mathbb {P}$
-name such that
$\mathbb {P}$
-name such that
Then no
![]() $S\in [\omega ]^{\omega }\cap V$
can
$S\in [\omega ]^{\omega }\cap V$
can
![]() $\varepsilon $
-almost bisect
$\varepsilon $
-almost bisect
![]() $\dot {X}$
.
$\dot {X}$
.
Proof Fix an
![]() $S\in [\omega ]^{\omega }$
, an
$S\in [\omega ]^{\omega }$
, an
![]() , and a
, and a
![]() $p\in \mathbb {P}$
. Pick an n in
$p\in \mathbb {P}$
. Pick an n in
![]() $\omega \smallsetminus \mathrm {dom}(p)$
such that
$\omega \smallsetminus \mathrm {dom}(p)$
such that
We distinguish two cases:
Case 1:
![]() $|S\cap I_n|>|I_n|/2$
. Define
$|S\cap I_n|>|I_n|/2$
. Define
![]() $q_n\in \mathbb {P}$
,
$q_n\in \mathbb {P}$
,
![]() $\mathrm {dom}(q_n)=\mathrm {dom}(p)\cup \{n\}$
,
$\mathrm {dom}(q_n)=\mathrm {dom}(p)\cup \{n\}$
,
![]() $q_n{\upharpoonright }_{\mathrm {dom}(p)}=p$
, and
$q_n{\upharpoonright }_{\mathrm {dom}(p)}=p$
, and
![]() $q_n(n)=S\cap I_n$
. Then
$q_n(n)=S\cap I_n$
. Then
![]() $q_n\leq p$
and
$q_n\leq p$
and
![]() $q_n$
forces that
$q_n$
forces that
 $$ \begin{align*} \frac{|S\cap \dot{X}\cap I_{\leq n}|}{|\dot{X}\cap I_{\leq n}|}&\geq \frac{|S\cap I_n|}{|I_{<n}|+|S\cap I_n|}= \frac{1}{\frac{|I_{<n}|}{|S\cap I_n|}+1}\\ &>\frac{1}{\frac{|I_{<n}|}{|I_n|/2}+1}>\frac{1}{2^{-n+1}+1}\geq \frac{1}{2}+\varepsilon\text{.} \end{align*} $$
$$ \begin{align*} \frac{|S\cap \dot{X}\cap I_{\leq n}|}{|\dot{X}\cap I_{\leq n}|}&\geq \frac{|S\cap I_n|}{|I_{<n}|+|S\cap I_n|}= \frac{1}{\frac{|I_{<n}|}{|S\cap I_n|}+1}\\ &>\frac{1}{\frac{|I_{<n}|}{|I_n|/2}+1}>\frac{1}{2^{-n+1}+1}\geq \frac{1}{2}+\varepsilon\text{.} \end{align*} $$
As n can be arbitrarily large, p cannot force that
![]() $S \ \varepsilon $
-almost bisects
$S \ \varepsilon $
-almost bisects
![]() $\dot {X}$
.
$\dot {X}$
.
Case 2:
![]() $|S\cap I_n|\leq |I_n|/2$
. Define
$|S\cap I_n|\leq |I_n|/2$
. Define
![]() $r_n\in \mathbb {P}$
,
$r_n\in \mathbb {P}$
,
![]() $\mathrm {dom}(r_n)=\mathrm {dom}(p)\cup \{n\}$
,
$\mathrm {dom}(r_n)=\mathrm {dom}(p)\cup \{n\}$
,
![]() $r_n{\upharpoonright }_{\mathrm {dom}(p)}=p$
, and
$r_n{\upharpoonright }_{\mathrm {dom}(p)}=p$
, and
![]() $r_n(n)=I_n\smallsetminus S$
. Then
$r_n(n)=I_n\smallsetminus S$
. Then
![]() $r_n\leq p$
and
$r_n\leq p$
and
![]() $r_n$
forces that
$r_n$
forces that
 $$ \begin{align*} \frac{|S\cap \dot{X}\cap I_{\leq n}|}{|\dot{X}\cap I_{\leq n}|}\leq \frac{|I_{<n}|}{|I_n\smallsetminus S|}\leq \frac{|I_{<n}|}{|I_n|/2}<2^{-n+1}\leq \frac{1}{2}-\varepsilon\text{.} \end{align*} $$
$$ \begin{align*} \frac{|S\cap \dot{X}\cap I_{\leq n}|}{|\dot{X}\cap I_{\leq n}|}\leq \frac{|I_{<n}|}{|I_n\smallsetminus S|}\leq \frac{|I_{<n}|}{|I_n|/2}<2^{-n+1}\leq \frac{1}{2}-\varepsilon\text{.} \end{align*} $$
As n can be arbitrarily large, p cannot force that
![]() $S \ \varepsilon $
-almost bisects
$S \ \varepsilon $
-almost bisects
![]() $\dot {X}$
.
$\dot {X}$
.
Applying this lemma and the aforementioned properties of
![]() $\mathbb {P}_{\omega _2}$
, we obtain the following:
$\mathbb {P}_{\omega _2}$
, we obtain the following:
Theorem 4.2. If
![]() , then
, then
![]() .
.
We show that this strict inequality can be obtained via a finite support iteration as well, namely, we can dualise (now in the forcing sense) the result saying that
![]() in the Hechler model (see Theorem 3.4). Consider the dual Hechler model, that is, every model of the form
in the Hechler model (see Theorem 3.4). Consider the dual Hechler model, that is, every model of the form
![]() $V^{\mathbb {D}_{\omega _1}}$
where
$V^{\mathbb {D}_{\omega _1}}$
where
![]() $V\vDash $
“
$V\vDash $
“
![]() .” We know (see, e.g., [Reference Blass1, Model 7.6.10]) that
.” We know (see, e.g., [Reference Blass1, Model 7.6.10]) that
![]() $\mathrm {cof}(\mathcal {M})=\omega _1$
holds in these models. We interpret
$\mathrm {cof}(\mathcal {M})=\omega _1$
holds in these models. We interpret
![]() $\mathbb {D}$
as the filter-based Laver forcing for the Fréchet filter over
$\mathbb {D}$
as the filter-based Laver forcing for the Fréchet filter over
![]() $\omega ^{\uparrow <\omega }=\{s\in \omega ^{<\omega } \mid s \text { is strictly increasing}\}$
, that is,
$\omega ^{\uparrow <\omega }=\{s\in \omega ^{<\omega } \mid s \text { is strictly increasing}\}$
, that is,
![]() $T\in \mathbb {D}$
if
$T\in \mathbb {D}$
if
![]() $T\subseteq \omega ^{\uparrow <\omega }$
is a tree (i.e., T is closed with regard to taking initial segments) with a fixed element
$T\subseteq \omega ^{\uparrow <\omega }$
is a tree (i.e., T is closed with regard to taking initial segments) with a fixed element
![]() $\mathrm {stem}(T)\in T$
such that:
$\mathrm {stem}(T)\in T$
such that:
-
(a) either
 $t\subseteq \mathrm {stem}(T)$
or
$t\subseteq \mathrm {stem}(T)$
or
 $\mathrm {stem}(T)\subseteq t$
for every
$\mathrm {stem}(T)\subseteq t$
for every
 $t\in T$
and
$t\in T$
and -
(b)
 $\mathrm {ext}_T(t)=\{n\in \omega \mid t^{\frown }(n)\in T\}$
is cofinite in
$\mathrm {ext}_T(t)=\{n\in \omega \mid t^{\frown }(n)\in T\}$
is cofinite in
 $\omega $
for every
$\omega $
for every
 $t\in T$
with
$t\in T$
with
 $\mathrm {stem}(T)\subseteq t$
.
$\mathrm {stem}(T)\subseteq t$
.
If
![]() $T\in \mathbb {D}$
and
$T\in \mathbb {D}$
and
![]() $s\in T$
, then let
$s\in T$
, then let
![]() $T{\upharpoonright }_{s}=\{t\in T \mid t\subseteq s \text { or } t\supseteq s\} \in \mathbb {D}$
. Let
$T{\upharpoonright }_{s}=\{t\in T \mid t\subseteq s \text { or } t\supseteq s\} \in \mathbb {D}$
. Let
![]() $\dot {d}$
be a
$\dot {d}$
be a
![]() $\mathbb {D}$
-name for the generic dominating real, i.e.,
$\mathbb {D}$
-name for the generic dominating real, i.e.,
![]() $\dot {d}=\bigcup \{\mathrm {stem}(T) \mid T \text { belongs to the generic } \text{filter}\}\in \omega ^{\uparrow \omega }=\{f\in \omega ^{\omega } \mid f \text { is strictly increasing}\}$
.
$\dot {d}=\bigcup \{\mathrm {stem}(T) \mid T \text { belongs to the generic } \text{filter}\}\in \omega ^{\uparrow \omega }=\{f\in \omega ^{\omega } \mid f \text { is strictly increasing}\}$
.
We recall a classical preservation theorem we will apply (see, e.g., [Reference Goldstern, Blass and Geschke6] or [Reference Blass1, Section 6.4]). Fix a sequence
![]() $(\sqsubset _n)_{n\in \omega }$
of increasing closed relations on
$(\sqsubset _n)_{n\in \omega }$
of increasing closed relations on
![]() $\omega ^{\omega }$
such that
$\omega ^{\omega }$
such that
for every n and g. Let
![]() $\sqsubset =\bigcup _{n\in \omega }\sqsubset _n$
. We will use terminology compatible with the one we use when working with relational systems: If
$\sqsubset =\bigcup _{n\in \omega }\sqsubset _n$
. We will use terminology compatible with the one we use when working with relational systems: If
![]() $\kappa =\mathrm {cof}(\kappa )>\omega $
, then a
$\kappa =\mathrm {cof}(\kappa )>\omega $
, then a
![]() $U\subseteq \omega ^{\omega }$
is
$U\subseteq \omega ^{\omega }$
is
![]() $\kappa $
-
$\kappa $
-
![]() $\sqsubset $
-unbounded if for every
$\sqsubset $
-unbounded if for every
![]() $C\subseteq \omega ^{\omega }$
of size
$C\subseteq \omega ^{\omega }$
of size
![]() $<\kappa $
, there is an
$<\kappa $
, there is an
![]() $f\in U$
which is not
$f\in U$
which is not
![]() $\sqsubset $
-below any element of C. In this case we will write
$\sqsubset $
-below any element of C. In this case we will write
![]() $f\not \sqsubset C$
.
$f\not \sqsubset C$
.
Definition 4.3. Let
![]() $\kappa =\mathrm {cof}(\kappa )>\omega $
and let
$\kappa =\mathrm {cof}(\kappa )>\omega $
and let
![]() $\mathbb {P}$
be a
$\mathbb {P}$
be a
![]() $\kappa $
-cc forcing notion. We say that
$\kappa $
-cc forcing notion. We say that
![]() $\mathbb {P}$
is
$\mathbb {P}$
is
![]() $\kappa $
-
$\kappa $
-
![]() $\sqsubset $
-good if for every
$\sqsubset $
-good if for every
![]() $\mathbb {P}$
-name
$\mathbb {P}$
-name
![]() $\dot {h}$
for an element of
$\dot {h}$
for an element of
![]() $\omega ^{\omega }$
, there exists a non-empty
$\omega ^{\omega }$
, there exists a non-empty
![]() $Y\subseteq \omega ^{\omega }$
of size
$Y\subseteq \omega ^{\omega }$
of size
![]() ${<}\kappa $
such that
${<}\kappa $
such that
![]() $\Vdash _{\mathbb {P}} f\not \sqsubset \dot {h}$
whenever
$\Vdash _{\mathbb {P}} f\not \sqsubset \dot {h}$
whenever
![]() $f\not \sqsubset Y$
. Say that
$f\not \sqsubset Y$
. Say that
![]() $\mathbb {P}$
is
$\mathbb {P}$
is
![]() $\sqsubset $
-good if it is
$\sqsubset $
-good if it is
![]() $\omega _1$
-
$\omega _1$
-
![]() $\sqsubset $
-good.Footnote
1
$\sqsubset $
-good.Footnote
1
It is straightforward to show that if
![]() $\mathbb {P}$
is
$\mathbb {P}$
is
![]() $\kappa $
-
$\kappa $
-
![]() $\sqsubset $
-good, then
$\sqsubset $
-good, then
![]() $\mathbb {P}$
preserves (a) “F is
$\mathbb {P}$
preserves (a) “F is
![]() $\kappa $
-
$\kappa $
-
![]() $\sqsubset $
-unbounded” for
$\sqsubset $
-unbounded” for
![]() $F\subseteq \omega ^{\omega }$
and (b) “
$F\subseteq \omega ^{\omega }$
and (b) “
![]() $\mathfrak {d}(\sqsubset )\geq \lambda $
” for cardinals
$\mathfrak {d}(\sqsubset )\geq \lambda $
” for cardinals
![]() $\lambda \geq \kappa $
(see [Reference Mejía9]).
$\lambda \geq \kappa $
(see [Reference Mejía9]).
Theorem 4.4 (see [Reference Judah and Shelah8] or [Reference Blass1, Lemma 6.4.12]).
Let
![]() $\kappa =\mathrm {cof}(\kappa )>\omega $
and assume that
$\kappa =\mathrm {cof}(\kappa )>\omega $
and assume that
![]() $(\mathbb {P}_{\alpha }, \dot {\mathbb {Q}}_{\beta } )_{\alpha \leq \delta , \beta <\delta }$
is a finite support iteration of
$(\mathbb {P}_{\alpha }, \dot {\mathbb {Q}}_{\beta } )_{\alpha \leq \delta , \beta <\delta }$
is a finite support iteration of
![]() $\kappa $
-cc forcing notions such that
$\kappa $
-cc forcing notions such that
![]() $\Vdash _{\alpha }\text {"}\,\dot {\mathbb {Q}}_{\alpha } \text { is } \kappa \text {-}\sqsubset \text {-good"}$
for every
$\Vdash _{\alpha }\text {"}\,\dot {\mathbb {Q}}_{\alpha } \text { is } \kappa \text {-}\sqsubset \text {-good"}$
for every
![]() $\alpha <\delta $
. Then
$\alpha <\delta $
. Then
![]() $\mathbb {P}_{\delta }$
is
$\mathbb {P}_{\delta }$
is
![]() $\kappa $
-
$\kappa $
-
![]() $\sqsubset $
-good as well.
$\sqsubset $
-good as well.
We are going to apply this theorem with
![]() $\dot {\mathbb {Q}}_{\alpha }=\mathbb {D}$
, but first we define our relation
$\dot {\mathbb {Q}}_{\alpha }=\mathbb {D}$
, but first we define our relation
![]() $\sqsubset $
. Fix an
$\sqsubset $
. Fix an
and an interval partition
![]() $(I_k)$
as we already did above, that is,
$(I_k)$
as we already did above, that is,
![]() $|I_0| \geq 2$
and
$|I_0| \geq 2$
and
![]() $|I_k|>2^k|I_{<k}|$
for every k. Let
$|I_k|>2^k|I_{<k}|$
for every k. Let
and define the relation
![]() $\sqsubset = \bigcup _{n\in \omega }\sqsubset _n$
on
$\sqsubset = \bigcup _{n\in \omega }\sqsubset _n$
on
![]() $[\omega ]^{\omega }\times \mathcal {O}$
by
$[\omega ]^{\omega }\times \mathcal {O}$
by
First of all, notice that
![]() $[\omega ]^{\omega }$
as a subspace of
$[\omega ]^{\omega }$
as a subspace of
![]() $\mathcal {P}(\omega )$
is canonically homeomorphic (denoted by
$\mathcal {P}(\omega )$
is canonically homeomorphic (denoted by
![]() $\simeq $
) to
$\simeq $
) to
![]() $\omega ^{\uparrow \omega }\subseteq \omega ^{\omega }$
and hence to
$\omega ^{\uparrow \omega }\subseteq \omega ^{\omega }$
and hence to
![]() $\omega ^{\omega }$
itself. To code
$\omega ^{\omega }$
itself. To code
![]() $\mathcal {O}$
as
$\mathcal {O}$
as
![]() $\omega ^{\omega }$
as well, let
$\omega ^{\omega }$
as well, let
 $$ \begin{align*} \mathcal{Q}_k=\left\{E \subseteq I_k \;\middle|\; \frac{|E|}{|I_k|}> \frac{1}{4}\right\}\!\text{;} \end{align*} $$
$$ \begin{align*} \mathcal{Q}_k=\left\{E \subseteq I_k \;\middle|\; \frac{|E|}{|I_k|}> \frac{1}{4}\right\}\!\text{;} \end{align*} $$
if we consider
![]() $\mathcal {Q}_k$
as a discrete space, then
$\mathcal {Q}_k$
as a discrete space, then
![]() $\prod _{k\in \omega }\mathcal {Q}_k$
is a compact metric space and
$\prod _{k\in \omega }\mathcal {Q}_k$
is a compact metric space and
Lemma 4.5. The following statements hold:
-
(1)
 $\mathrm {dom}(\sqsubset ) = [\omega ]^{\omega }$
and
$\mathrm {dom}(\sqsubset ) = [\omega ]^{\omega }$
and
 $\mathrm {ran}(\sqsubset ) = \mathcal {O}$
.
$\mathrm {ran}(\sqsubset ) = \mathcal {O}$
. -
(2) The relation
 $\sqsubset _n$
is closed in
$\sqsubset _n$
is closed in
 $[\omega ]^{\omega }\times \mathcal {O}$
.
$[\omega ]^{\omega }\times \mathcal {O}$
. -
(3) The set
 $(\sqsubset _n)^{(H,(E_k))}$
is nowhere dense in
$(\sqsubset _n)^{(H,(E_k))}$
is nowhere dense in
 $[\omega ]^{\omega }$
for every
$[\omega ]^{\omega }$
for every
 $(H, (E_k))\in \mathcal {O}$
.
$(H, (E_k))\in \mathcal {O}$
. -
(4)
 .
.
Proof (1): First let
![]() $X\in [\omega ]^{\omega }$
. If there is an infinite
$X\in [\omega ]^{\omega }$
. If there is an infinite
![]() $H\subseteq \omega $
such that
$H\subseteq \omega $
such that
![]() for every
for every
![]() $k\in H$
, then
$k\in H$
, then
![]() $X\sqsubset _1 (H,(I_k\smallsetminus X)_{k \in \omega })$
. If there is no such H, then
$X\sqsubset _1 (H,(I_k\smallsetminus X)_{k \in \omega })$
. If there is no such H, then
![]() for every
for every
![]() $k\geq K$
for some
$k\geq K$
for some
![]() $K\in \omega $
, and if we choose some
$K\in \omega $
, and if we choose some
![]() $E_k\subseteq I_k$
with
$E_k\subseteq I_k$
with
![]() for every
for every
![]() $k\geq K(\geq 2)$
, then
$k\geq K(\geq 2)$
, then
hence
![]() $X\sqsubset _0(\omega \smallsetminus K,(E_k)_{k \in \omega })$
.
$X\sqsubset _0(\omega \smallsetminus K,(E_k)_{k \in \omega })$
.
Now let
![]() $(H,(E_k)_{k \in \omega })\in \mathcal {O}$
. If
$(H,(E_k)_{k \in \omega })\in \mathcal {O}$
. If
![]() $X=\omega \smallsetminus \bigcup _{k\in H}E_k$
is infinite, then
$X=\omega \smallsetminus \bigcup _{k\in H}E_k$
is infinite, then
![]() $X\sqsubset _1 (H,(E_k))$
. If this set is finite, however, then there is a K such that
$X\sqsubset _1 (H,(E_k))$
. If this set is finite, however, then there is a K such that
![]() $\omega \smallsetminus K\subseteq H$
and
$\omega \smallsetminus K\subseteq H$
and
![]() $E_k=I_k$
for every
$E_k=I_k$
for every
![]() $k\geq K$
. If
$k\geq K$
. If
![]() $Y\in [\omega ]^{\omega }$
such that
$Y\in [\omega ]^{\omega }$
such that
![]() $|Y\cap I_k|=1$
for every k, then
$|Y\cap I_k|=1$
for every k, then
and so
![]() $Y\sqsubset _1 (H,(E_k))$
.
$Y\sqsubset _1 (H,(E_k))$
.
(2): If
![]() $X\not \sqsubset _n (H, (E_k))$
, then this is witnessed by a
$X\not \sqsubset _n (H, (E_k))$
, then this is witnessed by a
![]() $k_0\in H\smallsetminus n$
, that is,
$k_0\in H\smallsetminus n$
, that is,
Then
![]() $X'\not \sqsubset _n (H',(E^{\prime }_k))$
for all
$X'\not \sqsubset _n (H',(E^{\prime }_k))$
for all
![]() $X'\in [\omega ]^{\omega }$
and
$X'\in [\omega ]^{\omega }$
and
![]() $(H',(E^{\prime }_k))\in \mathcal {O}$
such that
$(H',(E^{\prime }_k))\in \mathcal {O}$
such that
![]() $X'\cap I_{k_0}=X\cap I_{k_0}$
,
$X'\cap I_{k_0}=X\cap I_{k_0}$
,
![]() $k_0\in H'$
, and
$k_0\in H'$
, and
![]() $E^{\prime }_{k_0}=E_{k_0}$
; these pairs
$E^{\prime }_{k_0}=E_{k_0}$
; these pairs
![]() $(X',(H',(E^{\prime }_k)))\in [\omega ]^{\omega }\times \mathcal {O}$
form an open neighbourhood of
$(X',(H',(E^{\prime }_k)))\in [\omega ]^{\omega }\times \mathcal {O}$
form an open neighbourhood of
![]() $(X,(H,(E_k)))$
in
$(X,(H,(E_k)))$
in
![]() $[\omega ]^{\omega }\times \mathcal {O}$
.
$[\omega ]^{\omega }\times \mathcal {O}$
.
(3): Fix an
![]() $X\in [\omega ]^{\omega }$
with
$X\in [\omega ]^{\omega }$
with
![]() $X\sqsubset _n(H,(E_k))$
and a basic open neighbourhood
$X\sqsubset _n(H,(E_k))$
and a basic open neighbourhood
![]() $U_m=\{Y\in [\omega ]^{\omega } \mid Y\cap m = X\cap m\}$
of X (for an
$U_m=\{Y\in [\omega ]^{\omega } \mid Y\cap m = X\cap m\}$
of X (for an
![]() $m\in \omega $
). If
$m\in \omega $
). If
![]() $k\in H\smallsetminus n$
such that
$k\in H\smallsetminus n$
such that
![]() $\min (I_k)\geq m$
(and k is sufficiently large, see below), and
$\min (I_k)\geq m$
(and k is sufficiently large, see below), and
![]() $Y\in U_m$
such that
$Y\in U_m$
such that
![]() $Y\cap I_k=E_k$
, then k witnesses
$Y\cap I_k=E_k$
, then k witnesses
![]() $Y\not \sqsubset _n (H,(E_k))$
, that is,
$Y\not \sqsubset _n (H,(E_k))$
, that is,
![]() because
because
 $$ \begin{align*} \frac{|E_k|}{|I_k|}>\Big(\frac{1}{2}+\varepsilon\Big)\Big(\frac{|E_k|}{|I_k|}+2^{-k}\Big) \end{align*} $$
$$ \begin{align*} \frac{|E_k|}{|I_k|}>\Big(\frac{1}{2}+\varepsilon\Big)\Big(\frac{|E_k|}{|I_k|}+2^{-k}\Big) \end{align*} $$
holds if k is sufficiently large.
(4):
![]() $\mathrm {cov}(\mathcal {M})\leq \mathfrak {d}(\sqsubset )$
follows from (1) and (3). Now let
$\mathrm {cov}(\mathcal {M})\leq \mathfrak {d}(\sqsubset )$
follows from (1) and (3). Now let
![]() $S\in [\omega ]^{\omega }$
, define
$S\in [\omega ]^{\omega }$
, define
![]() $S'=S$
if
$S'=S$
if
![]() for infinitely many k and
for infinitely many k and
![]() $S'=\omega \smallsetminus S$
otherwise, and let
$S'=\omega \smallsetminus S$
otherwise, and let
![]() . For
. For
![]() $k\in H_S$
, let
$k\in H_S$
, let
![]() $E^S_k=S'\cap I_k$
, and for
$E^S_k=S'\cap I_k$
, and for
![]() $k\in \omega \smallsetminus H_S$
, let
$k\in \omega \smallsetminus H_S$
, let
![]() $E_k=I_k$
. It is enough to show that if
$E_k=I_k$
. It is enough to show that if
![]() $S \ \varepsilon $
-almost bisects X, then
$S \ \varepsilon $
-almost bisects X, then
![]() $X\sqsubset (H_S,(E^S_k))$
, i.e., that
$X\sqsubset (H_S,(E^S_k))$
, i.e., that
![]() is a Tukey connection. Clearly,
is a Tukey connection. Clearly,
![]() iff
iff
![]() ; therefore if
; therefore if
![]() $k\in H_S$
is sufficiently large, then
$k\in H_S$
is sufficiently large, then
![]() $X\cap I_{\leq k}\neq \varnothing $
and
$X\cap I_{\leq k}\neq \varnothing $
and
 $$ \begin{align*} \frac{|X\cap E^{S}_k|}{|X\cap I_k|+|I_{<k}|} \leq \frac{|S'\cap X\cap I_{\leq k}|}{|X\cap I_{\leq k}|} < \frac{1}{2}+\varepsilon\text{,} \end{align*} $$
$$ \begin{align*} \frac{|X\cap E^{S}_k|}{|X\cap I_k|+|I_{<k}|} \leq \frac{|S'\cap X\cap I_{\leq k}|}{|X\cap I_{\leq k}|} < \frac{1}{2}+\varepsilon\text{,} \end{align*} $$
finishing the proof.
Lemma 4.6.
![]() $\mathbb {D}$
is
$\mathbb {D}$
is
![]() $\sqsubset $
-good.
$\sqsubset $
-good.
Proof Let
![]() $(\dot {H},(\dot {E}_k))$
be a
$(\dot {H},(\dot {E}_k))$
be a
![]() $\mathbb {D}$
-name for an element of
$\mathbb {D}$
-name for an element of
![]() $\mathcal {O}$
. We will construct a countable family
$\mathcal {O}$
. We will construct a countable family
![]() $\mathcal {O}'\subseteq \mathcal {O}$
such that whenever
$\mathcal {O}'\subseteq \mathcal {O}$
such that whenever
![]() $X\in [\omega ]^{\omega }\cap V$
and
$X\in [\omega ]^{\omega }\cap V$
and
![]() $X\not \sqsubset \mathcal {O}'$
, then
$X\not \sqsubset \mathcal {O}'$
, then
![]() $\Vdash X\not \sqsubset (\dot {H},(\dot {E}_k))$
.
$\Vdash X\not \sqsubset (\dot {H},(\dot {E}_k))$
.
Let
![]() $\dot {H}=\{\dot {k}_0<\dot {k}_1<\cdots \}$
be an enumeration in
$\dot {H}=\{\dot {k}_0<\dot {k}_1<\cdots \}$
be an enumeration in
![]() $V^{\mathbb {D}}$
. Recall that we denote the generic real of
$V^{\mathbb {D}}$
. Recall that we denote the generic real of
![]() $\mathbb {D}$
by
$\mathbb {D}$
by
![]() $\dot {d}$
. By thinning out
$\dot {d}$
. By thinning out
![]() $\dot {H}$
, we can assume that
$\dot {H}$
, we can assume that
![]() $\dot {d}(n) < \dot {k}_n$
for every n. (Note that if
$\dot {d}(n) < \dot {k}_n$
for every n. (Note that if
![]() $\Vdash X\not \sqsubset (\dot {J},(\dot {E}_k))$
for some infinite
$\Vdash X\not \sqsubset (\dot {J},(\dot {E}_k))$
for some infinite
![]() $\dot {J}\subseteq \dot {H}$
, then this holds for
$\dot {J}\subseteq \dot {H}$
, then this holds for
![]() $\dot {H}$
as well.)
$\dot {H}$
as well.)
We define a rank function
![]() $\rho _n$
on
$\rho _n$
on
![]() $\omega ^{<\uparrow \omega }$
for every fixed
$\omega ^{<\uparrow \omega }$
for every fixed
![]() $n\in \omega $
as follows: We set
$n\in \omega $
as follows: We set
![]() $\rho _n(s)=0$
if there are
$\rho _n(s)=0$
if there are
![]() $k_{n,s}\in \omega $
and
$k_{n,s}\in \omega $
and
![]() $E_{n,s}\subseteq I_{k_{n,s}}$
such that whenever
$E_{n,s}\subseteq I_{k_{n,s}}$
such that whenever
![]() $T\in \mathbb {D}$
and
$T\in \mathbb {D}$
and
![]() $\mathrm {stem}(T)=s$
, then there is a
$\mathrm {stem}(T)=s$
, then there is a
![]() $T'\leq T$
which forces that “
$T'\leq T$
which forces that “
![]() $\dot {k}_n=k_{n,s}$
and
$\dot {k}_n=k_{n,s}$
and
![]() $\dot {E}_{k_{n,s}}=E_{n,s}$
.” Then we proceed by recursion: At the
$\dot {E}_{k_{n,s}}=E_{n,s}$
.” Then we proceed by recursion: At the
![]() $\alpha $
th stage, after already having defined
$\alpha $
th stage, after already having defined
![]() $\{s\in \omega ^{<\omega } \mid \rho _n(s)=\beta \}$
for every
$\{s\in \omega ^{<\omega } \mid \rho _n(s)=\beta \}$
for every
![]() $\beta <\alpha $
, we set
$\beta <\alpha $
, we set
![]() $\rho _n(s)=\alpha $
if
$\rho _n(s)=\alpha $
if
We show that
![]() $\mathrm {dom}(\rho _n)=\omega ^{<\uparrow \omega }$
for every n. Assume towards a contradiction that
$\mathrm {dom}(\rho _n)=\omega ^{<\uparrow \omega }$
for every n. Assume towards a contradiction that
![]() $\rho _n(s)$
is not defined. Then
$\rho _n(s)$
is not defined. Then
![]() $\{m \mid \rho _n(s^{\frown }(m))\text { is not defined}\}$
is cofinite; hence we can construct a
$\{m \mid \rho _n(s^{\frown }(m))\text { is not defined}\}$
is cofinite; hence we can construct a
![]() $T\in \mathbb {D}$
with stem s such that
$T\in \mathbb {D}$
with stem s such that
![]() $\rho _n(t)$
is not defined for every
$\rho _n(t)$
is not defined for every
![]() $t\in T$
above s. There are a
$t\in T$
above s. There are a
![]() $T'\leq T$
,
$T'\leq T$
,
![]() $k\in \omega $
, and
$k\in \omega $
, and
![]() $E\subseteq I_k$
such that
$E\subseteq I_k$
such that
![]() $T'\Vdash \text {"}\dot {k}_n=k$
and
$T'\Vdash \text {"}\dot {k}_n=k$
and
![]() $\dot {E}_k=E \text {"}$
; in particular, k and E witness that
$\dot {E}_k=E \text {"}$
; in particular, k and E witness that
![]() $\rho _n(\mathrm {stem}(T'))=0$
, a contradiction.
$\rho _n(\mathrm {stem}(T'))=0$
, a contradiction.
Also, we will need the fact that if
![]() $n\geq |s|$
, then
$n\geq |s|$
, then
![]() $\rho _n(s)>0$
. To see this, let (for
$\rho _n(s)>0$
. To see this, let (for
![]() $k\in \omega $
)
$k\in \omega $
)
![]() $T_k\in \mathbb {D}$
such that
$T_k\in \mathbb {D}$
such that
![]() $\mathrm {stem}(T_k)=s$
and
$\mathrm {stem}(T_k)=s$
and
![]() $\mathrm {ext}_{T_k}(s)=\omega \smallsetminus k$
. Then
$\mathrm {ext}_{T_k}(s)=\omega \smallsetminus k$
. Then
![]() $T_k\Vdash k\leq \dot {d}(|s|)\leq \dot {d}(n)<\dot {k}_n$
. If
$T_k\Vdash k\leq \dot {d}(|s|)\leq \dot {d}(n)<\dot {k}_n$
. If
![]() $\rho _n(s)=0$
, then we could pick
$\rho _n(s)=0$
, then we could pick
![]() $k_{n,s}$
such that
$k_{n,s}$
such that
![]() $T\Vdash \dot {k}_n=k_{n,s}$
whenever
$T\Vdash \dot {k}_n=k_{n,s}$
whenever
![]() $T\in \mathbb {D}$
with stem s; but in that case,
$T\in \mathbb {D}$
with stem s; but in that case,
![]() $T=T_{k_{n,s}}\Vdash k_{n,s}<\dot {k}_n$
, a contradiction.
$T=T_{k_{n,s}}\Vdash k_{n,s}<\dot {k}_n$
, a contradiction.
Now, if
![]() $\rho _n(s)=1$
and
$\rho _n(s)=1$
and
![]() $m\in Y_{n,s}$
, then
$m\in Y_{n,s}$
, then
![]() $\rho _n(s^{\frown }(m))=0$
and hence we have defined
$\rho _n(s^{\frown }(m))=0$
and hence we have defined
![]() $k_{n,s^{\frown }(m)}$
and
$k_{n,s^{\frown }(m)}$
and
![]() $E_{n,s^{\frown }(m)}$
. Note that
$E_{n,s^{\frown }(m)}$
. Note that
for each k. Otherwise, there are
![]() $k \in \omega $
and
$k \in \omega $
and
![]() $E\subseteq I_k$
such that
$E\subseteq I_k$
such that
![]() $X=\{m\in Y_{n,s} \mid k_{n,s^{\frown }(m)}=k \text { and } E_{n,s^{\frown }(m)}=E\}$
is also infinite, and hence if
$X=\{m\in Y_{n,s} \mid k_{n,s^{\frown }(m)}=k \text { and } E_{n,s^{\frown }(m)}=E\}$
is also infinite, and hence if
![]() $T\in \mathbb {D}$
with
$T\in \mathbb {D}$
with
![]() $\mathrm {stem}(T)=s$
, then there is an
$\mathrm {stem}(T)=s$
, then there is an
![]() $m\in X\cap \mathrm {ext}_T(s)$
, and so there is a
$m\in X\cap \mathrm {ext}_T(s)$
, and so there is a
![]() $T'\leq T {\upharpoonright }_{s^{\frown }(m)} \leq T$
such that
$T'\leq T {\upharpoonright }_{s^{\frown }(m)} \leq T$
such that
![]() $T'\Vdash \text {"} \dot {k}_n=k \text { and } \dot {E}_{k}=E \text {,"}$
in other words,
$T'\Vdash \text {"} \dot {k}_n=k \text { and } \dot {E}_{k}=E \text {,"}$
in other words,
![]() $\rho _n(s)=0$
, a contradiction.
$\rho _n(s)=0$
, a contradiction.
For such n and s we can thus fix an infinite
![]() $Z_{n,s}\subseteq Y_{n,s}$
such that
$Z_{n,s}\subseteq Y_{n,s}$
such that
We let
![]() $K_{n,s} = \{k_{n,s^{\frown }(m)} \mid m\in Z_{n,s}\}$
,
$K_{n,s} = \{k_{n,s^{\frown }(m)} \mid m\in Z_{n,s}\}$
,
![]() $E^{n,s}_k=E_{n,s^{\frown }(m)}$
if
$E^{n,s}_k=E_{n,s^{\frown }(m)}$
if
![]() $m\in Z_{n,s}$
and
$m\in Z_{n,s}$
and
![]() $k_{n,s^{\frown }(m)}=k$
and
$k_{n,s^{\frown }(m)}=k$
and
![]() $E^{n,s}_k=I_k$
otherwise, and
$E^{n,s}_k=I_k$
otherwise, and
To finish the proof, fix an
![]() $X \in [\omega ]^{\omega }\cap V$
and assume that
$X \in [\omega ]^{\omega }\cap V$
and assume that
![]() $X \not \sqsubset \mathcal {O}'$
, i.e.,
$X \not \sqsubset \mathcal {O}'$
, i.e.,
![]() $X\not \sqsubset (K_{n,s},(E^{n,s}_k))$
whenever
$X\not \sqsubset (K_{n,s},(E^{n,s}_k))$
whenever
![]() $\rho _n(s)=1$
, or more explicitly, for infinitely many
$\rho _n(s)=1$
, or more explicitly, for infinitely many
![]() $k\in K_{n,s}$
$k\in K_{n,s}$
To show that
![]() $\Vdash X\not \sqsubset (\dot {H},(\dot {E}_k))$
, we fix
$\Vdash X\not \sqsubset (\dot {H},(\dot {E}_k))$
, we fix
![]() $T\in \mathbb {D}$
and
$T\in \mathbb {D}$
and
![]() $n\in \omega $
. We will find a
$n\in \omega $
. We will find a
![]() $T'\leq T$
and a
$T'\leq T$
and a
![]() $k\geq n$
such that
$k\geq n$
such that
![]() $T' \Vdash \text {"} k\in \dot {H} \text { and } (\bullet _{k,X,(\dot {E}_k)})\text {."}$
We can assume that
$T' \Vdash \text {"} k\in \dot {H} \text { and } (\bullet _{k,X,(\dot {E}_k)})\text {."}$
We can assume that
![]() $n\geq |\mathrm {stem}(T)|$
and hence
$n\geq |\mathrm {stem}(T)|$
and hence
![]() $\rho _n(\mathrm {stem}(T))>0$
. By induction on this rank, one can easily show that there is an
$\rho _n(\mathrm {stem}(T))>0$
. By induction on this rank, one can easily show that there is an
![]() $s\in T$
above the stem such that
$s\in T$
above the stem such that
![]() $\rho _n(s)=1$
. Pick a
$\rho _n(s)=1$
. Pick a
![]() $k=k_{n,s^{\frown }(m)}\in K_{n,s}\cap \mathrm {ext}_T(s)\smallsetminus n$
such that
$k=k_{n,s^{\frown }(m)}\in K_{n,s}\cap \mathrm {ext}_T(s)\smallsetminus n$
such that
![]() $(\bullet _{k,X,(E^{n,s}_k)})$
. By the definition of
$(\bullet _{k,X,(E^{n,s}_k)})$
. By the definition of
![]() $\rho _n(s^{\frown }(m))=0$
, there is a
$\rho _n(s^{\frown }(m))=0$
, there is a
![]() $T' \leq T{\upharpoonright }_{s^{\frown }(m)} \leq T$
which forces that
$T' \leq T{\upharpoonright }_{s^{\frown }(m)} \leq T$
which forces that
![]() $\dot {k}_n=k$
and
$\dot {k}_n=k$
and
![]() $\dot {E}_k=E_{n,s^{\frown }(m)}=E^{n,s}_k$
; in particular,
$\dot {E}_k=E_{n,s^{\frown }(m)}=E^{n,s}_k$
; in particular,
![]() $T'$
also forces that
$T'$
also forces that
![]() $k\in \dot {H}\smallsetminus n$
and
$k\in \dot {H}\smallsetminus n$
and
![]() $(\bullet _{k,X,(\dot {E}_k)})$
.
$(\bullet _{k,X,(\dot {E}_k)})$
.
Applying Lemma 4.6 and Theorem 4.4, we obtain that
![]() $\mathbb {D}_{\delta }$
preserves
$\mathbb {D}_{\delta }$
preserves
![]() , and hence the following:
, and hence the following:
Theorem 4.7. If
![]() , then
, then
![]() .
.
5 Further generalisations:
 $\mathfrak {s}_{\rho }$
and
$\mathfrak {s}_{\rho }$
and
 $\mathfrak {r}_{\rho }$
$\mathfrak {r}_{\rho }$
In this last section, we take a look at generalisations of
![]() and
and
![]() , in the following sense: For
, in the following sense: For
![]() $\rho \in (0,1)$
, let
$\rho \in (0,1)$
, let
![]() where
where
![]() $S \mid _{\rho } X$
(“
$S \mid _{\rho } X$
(“
![]() $S \ \rho $
-splits X”) if
$S \ \rho $
-splits X”) if
 $$ \begin{align*} \frac{|S \cap X \cap n|}{|X \cap n|}\xrightarrow{n\to\infty} \rho\text{.} \end{align*} $$
$$ \begin{align*} \frac{|S \cap X \cap n|}{|X \cap n|}\xrightarrow{n\to\infty} \rho\text{.} \end{align*} $$
We write
![]() $\mathfrak {s}_{\rho }=\mathfrak {b}(\mathbf {Reap}_{\rho })$
and
$\mathfrak {s}_{\rho }=\mathfrak {b}(\mathbf {Reap}_{\rho })$
and
![]() $\mathfrak {r}_{\rho }=\mathfrak {d}(\mathbf {Reap}_{\rho })$
.
$\mathfrak {r}_{\rho }=\mathfrak {d}(\mathbf {Reap}_{\rho })$
.
Obviously,
![]() $\mathbf {Reap}_{1-\rho }\equiv \mathbf {Reap}_{\rho }\preccurlyeq \mathbf {Reap}$
and hence
$\mathbf {Reap}_{1-\rho }\equiv \mathbf {Reap}_{\rho }\preccurlyeq \mathbf {Reap}$
and hence
![]() $\mathfrak {s}_{\rho }=\mathfrak {s}_{1-\rho }\geq \mathfrak {s}$
and
$\mathfrak {s}_{\rho }=\mathfrak {s}_{1-\rho }\geq \mathfrak {s}$
and
![]() $\mathfrak {r}_{\rho }=\mathfrak {r}_{1-\rho }\leq \mathfrak {r}$
for all
$\mathfrak {r}_{\rho }=\mathfrak {r}_{1-\rho }\leq \mathfrak {r}$
for all
![]() $\rho \in (0,1)$
. We will need the following easy observation:
$\rho \in (0,1)$
. We will need the following easy observation:
Fact 5.1. Let
![]() $\rho _0,\rho _1\in (0,1)$
and
$\rho _0,\rho _1\in (0,1)$
and
![]() $A,B,X\in [\omega ]^{\omega }$
. Then the following statements hold:
$A,B,X\in [\omega ]^{\omega }$
. Then the following statements hold:
-
(1) If
 $A\mid _{\rho _0} X$
and
$A\mid _{\rho _0} X$
and
 $B\mid _{\rho _1} A\cap X$
, then
$B\mid _{\rho _1} A\cap X$
, then
 $A\cap B\mid _{\rho _0\rho _1} X$
; hence
$A\cap B\mid _{\rho _0\rho _1} X$
; hence
 $\max \{\mathfrak {s}_{\rho _0},\mathfrak {s}_{\rho _1}\}\geq \mathfrak {s}_{\rho _0\rho _1}$
and
$\max \{\mathfrak {s}_{\rho _0},\mathfrak {s}_{\rho _1}\}\geq \mathfrak {s}_{\rho _0\rho _1}$
and
 $\min \{\mathfrak {r}_{\rho _0},\mathfrak {r}_{\rho _1}\}\leq \mathfrak {r}_{\rho _0\rho _1}$
.
$\min \{\mathfrak {r}_{\rho _0},\mathfrak {r}_{\rho _1}\}\leq \mathfrak {r}_{\rho _0\rho _1}$
. -
(2) If
 $A\mid _{\rho _0} X$
and
$A\mid _{\rho _0} X$
and
 $B\mid _{\rho _1} X\smallsetminus A$
, then
$B\mid _{\rho _1} X\smallsetminus A$
, then
 $A\cup B\mid _{\rho _0+\rho _1-\rho _0\rho _1} X$
; hence
$A\cup B\mid _{\rho _0+\rho _1-\rho _0\rho _1} X$
; hence
 $\max \{\mathfrak {s}_{\rho _0},\mathfrak {s}_{\rho _1}\}\geq \mathfrak {s}_{\rho _0+\rho _1-\rho _0\rho _1}$
and
$\max \{\mathfrak {s}_{\rho _0},\mathfrak {s}_{\rho _1}\}\geq \mathfrak {s}_{\rho _0+\rho _1-\rho _0\rho _1}$
and
 $\min \{\mathfrak {r}_{\rho _0},\mathfrak {r}_{\rho _1}\}\leq \mathfrak {r}_{\rho _0+\rho _1-\rho _0\rho _1}$
.
$\min \{\mathfrak {r}_{\rho _0},\mathfrak {r}_{\rho _1}\}\leq \mathfrak {r}_{\rho _0+\rho _1-\rho _0\rho _1}$
.
Proof (1) follows from
 $$ \begin{align*} \frac{|(A\cap B)\cap X\cap n|}{|X\cap n|}=\frac{|B\cap (A\cap X)\cap n|}{|(A\cap X)\cap n|}\cdot\frac{|A\cap X\cap n|}{|X\cap n|}\text{,} \end{align*} $$
$$ \begin{align*} \frac{|(A\cap B)\cap X\cap n|}{|X\cap n|}=\frac{|B\cap (A\cap X)\cap n|}{|(A\cap X)\cap n|}\cdot\frac{|A\cap X\cap n|}{|X\cap n|}\text{,} \end{align*} $$
and (2) follows from
 $$ \begin{align*} \frac{|(A\cup B)\cap X\cap n|}{|X\cap n|}&=\frac{|A\cap X\cap n|+ |B\cap (X\smallsetminus A)\cap n|}{|X\cap n|}\\ &=\frac{|A\cap X\cap n|}{|X\cap n|}+\frac{|B\cap (X\smallsetminus A)\cap n|}{|(X\smallsetminus A)\cap n|}\cdot\frac{|(X\smallsetminus A)\cap n|}{|X\cap n|}\text{.}\\[-42pt] \end{align*} $$
$$ \begin{align*} \frac{|(A\cup B)\cap X\cap n|}{|X\cap n|}&=\frac{|A\cap X\cap n|+ |B\cap (X\smallsetminus A)\cap n|}{|X\cap n|}\\ &=\frac{|A\cap X\cap n|}{|X\cap n|}+\frac{|B\cap (X\smallsetminus A)\cap n|}{|(X\smallsetminus A)\cap n|}\cdot\frac{|(X\smallsetminus A)\cap n|}{|X\cap n|}\text{.}\\[-42pt] \end{align*} $$
Also, we recall a classical construction:
Fact 5.2 (Non-integer bases).
Let
![]() $b>1$
be a real number. Then every
$b>1$
be a real number. Then every
![]() $x>0$
can be written as
$x>0$
can be written as
![]() $x=\sum _{n=-\infty }^Nc_nb^n$
where
$x=\sum _{n=-\infty }^Nc_nb^n$
where
![]() $N\geq 0$
is an integer and
$N\geq 0$
is an integer and
![]() $0\leq c_n< b$
are also integers for all n.
$0\leq c_n< b$
are also integers for all n.
Theorem 5.3.
![]() $\mathfrak {r}_{\rho }$
does not depend on
$\mathfrak {r}_{\rho }$
does not depend on
![]() $\rho $
.
$\rho $
.
Proof Fix a
![]() . We show that
. We show that
![]() .
.
To show that
![]() , let
, let
![]() $\mathcal {R} \subseteq [\omega ]^{\omega }$
such that
$\mathcal {R} \subseteq [\omega ]^{\omega }$
such that
![]() . We will construct an
. We will construct an
![]() $S \in [\omega ]^{\omega }$
such that
$S \in [\omega ]^{\omega }$
such that
![]() $S \mid _{\rho } \mathcal {R}$
(that is, such that
$S \mid _{\rho } \mathcal {R}$
(that is, such that
![]() $S \mid _{\rho } X$
for every
$S \mid _{\rho } X$
for every
![]() $X\in \mathcal {R}$
).
$X\in \mathcal {R}$
).
By recursion on
![]() $n\in \omega $
, one can easily construct
$n\in \omega $
, one can easily construct
![]() $S_n\in [\omega ]^{\omega }$
and
$S_n\in [\omega ]^{\omega }$
and
![]() $\mathcal {R}_n \subseteq [\omega ]^{\omega }$
such that
$\mathcal {R}_n \subseteq [\omega ]^{\omega }$
such that
![]() $S_0=\omega $
,
$S_0=\omega $
,
![]() $\mathcal {R}_0=\mathcal {R}$
,
$\mathcal {R}_0=\mathcal {R}$
,
![]() and
and
For
![]() $m \geq 1$
, define
$m \geq 1$
, define
It follows that
![]() $\mathcal {R}_m=\{I_m\cap X \mid X\in \mathcal {R}\}$
and hence that
$\mathcal {R}_m=\{I_m\cap X \mid X\in \mathcal {R}\}$
and hence that
![]() $I_m,D_m\in [\omega ]^{\omega }$
for every
$I_m,D_m\in [\omega ]^{\omega }$
for every
![]() $m\geq 1$
. First of all, we show that
$m\geq 1$
. First of all, we show that
![]() and
and
![]() for every
for every
![]() $m\geq 1$
. This holds for
$m\geq 1$
. This holds for
![]() $m=1$
by the definitions above. We proceed by induction on m; assume that the claim holds for a fixed m. If
$m=1$
by the definitions above. We proceed by induction on m; assume that the claim holds for a fixed m. If
![]() $X\in \mathcal {R}$
, then
$X\in \mathcal {R}$
, then
![]() $I_m\cap X \in \mathcal {R}_m$
and thus
$I_m\cap X \in \mathcal {R}_m$
and thus
![]() . Since
. Since
![]() holds as well, we can apply Fact 5.1(1) with
holds as well, we can apply Fact 5.1(1) with
![]() ,
,
![]() ,
,
![]() $A=I_m$
,
$A=I_m$
,
![]() $B=S_{m+1}$
, and X, and obtain that
$B=S_{m+1}$
, and X, and obtain that
![]() . It follows that
. It follows that
![]() (because
(because
![]() ).
).
Now let
![]() $P \subseteq \omega \smallsetminus \{0\}$
be such that
$P \subseteq \omega \smallsetminus \{0\}$
be such that
![]() $\sum _{m \in P}{2^{-m}} = \rho $
(a representation of
$\sum _{m \in P}{2^{-m}} = \rho $
(a representation of
![]() $\rho <1$
in base
$\rho <1$
in base
![]() $2$
) and
$2$
) and
![]() $S= \bigcup _{m\in P}{D_m}$
. We show that
$S= \bigcup _{m\in P}{D_m}$
. We show that
![]() $S \mid _{\rho } \mathcal {R}$
. Fix an
$S \mid _{\rho } \mathcal {R}$
. Fix an
![]() $X\in \mathcal {R}$
and define the lower and upper relative density of
$X\in \mathcal {R}$
and define the lower and upper relative density of
![]() $S\in [\omega ]^{\omega }$
in
$S\in [\omega ]^{\omega }$
in
![]() $X\in [\omega ]^{\omega }$
as follows:
$X\in [\omega ]^{\omega }$
as follows:
 $$ \begin{align*} \overline{d}_X(S)&=\limsup_{n\to\infty}\frac{|S\cap X\cap n|}{|X\cap n|}\text{,}\\ \underline{d}_X(S)&=\liminf_{n\to\infty}\frac{|S\cap X\cap n|}{|X\cap n|}\text{.} \end{align*} $$
$$ \begin{align*} \overline{d}_X(S)&=\limsup_{n\to\infty}\frac{|S\cap X\cap n|}{|X\cap n|}\text{,}\\ \underline{d}_X(S)&=\liminf_{n\to\infty}\frac{|S\cap X\cap n|}{|X\cap n|}\text{.} \end{align*} $$
Clearly,
![]() $\overline {d}_X$
and
$\overline {d}_X$
and
![]() $\underline {d}_X$
are monotone,
$\underline {d}_X$
are monotone,
![]() $\overline {d}_X(\omega \smallsetminus S)=1-\underline {d}_X(S)$
and
$\overline {d}_X(\omega \smallsetminus S)=1-\underline {d}_X(S)$
and
![]() $\underline {d}_X(\omega \smallsetminus S)=1-\overline {d}_X(S)$
, and
$\underline {d}_X(\omega \smallsetminus S)=1-\overline {d}_X(S)$
, and
![]() $S \mid _{\rho } X$
iff
$S \mid _{\rho } X$
iff
![]() $\overline {d}_X(S)=\underline {d}_X(S)=\rho $
; in this case we write
$\overline {d}_X(S)=\underline {d}_X(S)=\rho $
; in this case we write
![]() $d_X(S)=\rho $
. Also, notice that
$d_X(S)=\rho $
. Also, notice that
![]() $d_X$
is finitely additive. It follows that it is enough to show that
$d_X$
is finitely additive. It follows that it is enough to show that
![]() $\underline {d}_X(S)\geq \rho $
and
$\underline {d}_X(S)\geq \rho $
and
![]() $\underline {d}_X(\omega \smallsetminus S) \geq 1-\rho $
. For
$\underline {d}_X(\omega \smallsetminus S) \geq 1-\rho $
. For
![]() $k\in \omega $
, let
$k\in \omega $
, let
![]() $A_k=\bigcup _{m\in P\cap k}D_m$
(and
$A_k=\bigcup _{m\in P\cap k}D_m$
(and
![]() $\bigcup \varnothing =\varnothing $
), then
$\bigcup \varnothing =\varnothing $
), then
![]() $\underline {d}_X(A_k)\leq \underline {d}_X(S)$
, and at the same time
$\underline {d}_X(A_k)\leq \underline {d}_X(S)$
, and at the same time
![]() $\underline {d}_X(A_k)=d_X(A_k)=\sum _{m\in P\cap k}d_X(D_m)=\sum _{m\in P\cap k}2^{-m}\xrightarrow {k\to \infty }\rho $
, hence
$\underline {d}_X(A_k)=d_X(A_k)=\sum _{m\in P\cap k}d_X(D_m)=\sum _{m\in P\cap k}2^{-m}\xrightarrow {k\to \infty }\rho $
, hence
![]() $\rho \leq \underline {d}_X(S)$
. To show that
$\rho \leq \underline {d}_X(S)$
. To show that
![]() $\underline {d}_X(\omega \smallsetminus S)\geq 1-\rho $
, write
$\underline {d}_X(\omega \smallsetminus S)\geq 1-\rho $
, write
![]() $\omega \smallsetminus S$
as
$\omega \smallsetminus S$
as
![]() $\bigcup _{m\in \omega \smallsetminus P}D_m$
. (Since finite modifications of
$\bigcup _{m\in \omega \smallsetminus P}D_m$
. (Since finite modifications of
![]() $S_n$
do not affect the above, we can assume without loss of generality that
$S_n$
do not affect the above, we can assume without loss of generality that
![]() $\bigcap _{n\in \omega }S_n=\varnothing $
and hence that
$\bigcap _{n\in \omega }S_n=\varnothing $
and hence that
![]() $\omega =\bigcup _{m\geq 1}D_m$
is a partition.)
$\omega =\bigcup _{m\geq 1}D_m$
is a partition.)
The proof of the converse inequality is similar but with a little twist: We start with a family
![]() $\mathcal {R}'\subseteq [\omega ]^{\omega }$
such that
$\mathcal {R}'\subseteq [\omega ]^{\omega }$
such that
![]() $|\mathcal {R}'| < \mathfrak {r}_{\rho }$
and have to construct an
$|\mathcal {R}'| < \mathfrak {r}_{\rho }$
and have to construct an
![]() $S' \in [\omega ]^{\omega }$
such that
$S' \in [\omega ]^{\omega }$
such that
![]() . By recursion on
. By recursion on
![]() $n\in \omega $
, we define
$n\in \omega $
, we define
![]() $S^{\prime }_n\in [\omega ]^{\omega }$
and
$S^{\prime }_n\in [\omega ]^{\omega }$
and
![]() $\mathcal {R}^{\prime }_n \subseteq [\omega ]^{\omega }$
such that
$\mathcal {R}^{\prime }_n \subseteq [\omega ]^{\omega }$
such that
![]() $S^{\prime }_0=\omega $
,
$S^{\prime }_0=\omega $
,
![]() $\mathcal {R}^{\prime }_0=\mathcal {R}'$
,
$\mathcal {R}^{\prime }_0=\mathcal {R}'$
,
![]() $S^{\prime }_{n+1}\mid _{\rho }\mathcal {R}^{\prime }_n$
, and
$S^{\prime }_{n+1}\mid _{\rho }\mathcal {R}^{\prime }_n$
, and
![]() $\mathcal {R}^{\prime }_{n+1} = \{S^{\prime }_{n+1} \cap X \mid X \in \mathcal {R}^{\prime }_n\}$
. For
$\mathcal {R}^{\prime }_{n+1} = \{S^{\prime }_{n+1} \cap X \mid X \in \mathcal {R}^{\prime }_n\}$
. For
![]() $m \geq 1$
, define
$m \geq 1$
, define
![]() $I^{\prime }_m=\bigcap _{n\leq m}S_n$
and
$I^{\prime }_m=\bigcap _{n\leq m}S_n$
and
![]() $D^{\prime }_m=I_{m-1} \smallsetminus I_m$
. It follows (by induction) that
$D^{\prime }_m=I_{m-1} \smallsetminus I_m$
. It follows (by induction) that
![]() $I^{\prime }_m \mid _{\rho ^m} \mathcal {R}'$
and
$I^{\prime }_m \mid _{\rho ^m} \mathcal {R}'$
and
![]() $D^{\prime }_m \mid _{\rho ^{m-1}(1-\rho )} \mathcal {R}'$
for every
$D^{\prime }_m \mid _{\rho ^{m-1}(1-\rho )} \mathcal {R}'$
for every
![]() $m\geq 1$
. If we can find a
$m\geq 1$
. If we can find a
![]() $P' \subseteq \omega \smallsetminus \{0\}$
such that
$P' \subseteq \omega \smallsetminus \{0\}$
such that
![]() , then, just like above,
, then, just like above,
![]() . The problem is that when writing
. The problem is that when writing
![]() in the non-integer base
in the non-integer base
![]() $1<b=\rho ^{-1}<2$
, i.e.,
$1<b=\rho ^{-1}<2$
, i.e.,
![]() , we may have to use non-zero coefficients for at least some
, we may have to use non-zero coefficients for at least some
![]() $0 \leq n \leq N$
. Therefore, we have two cases:
$0 \leq n \leq N$
. Therefore, we have two cases:
Case 1: If
![]() , i.e.,
, i.e.,
![]() , then
, then
![]() $N<0$
and we can pick an appropriate
$N<0$
and we can pick an appropriate
![]() $P'$
and hence conclude that
$P'$
and hence conclude that
![]() .
.
Case 2: If
![]() then, applying Fact 5.1(1),
then, applying Fact 5.1(1),
![]() $\mathfrak {r}_{\rho }=\min \{\mathfrak {r}_{\rho },\mathfrak {r}_{\rho }\}\leq \mathfrak {r}_{\rho ^2}=\min \{\mathfrak {r}_{\rho ^2},\mathfrak {r}_{\rho ^2}\}\leq \mathfrak {r}_{\rho ^4}\leq \cdots $
; in other words,
$\mathfrak {r}_{\rho }=\min \{\mathfrak {r}_{\rho },\mathfrak {r}_{\rho }\}\leq \mathfrak {r}_{\rho ^2}=\min \{\mathfrak {r}_{\rho ^2},\mathfrak {r}_{\rho ^2}\}\leq \mathfrak {r}_{\rho ^4}\leq \cdots $
; in other words,
![]() $\mathfrak {r}_{\rho }\leq \mathfrak {r}_{\rho ^2}\leq \mathfrak {r}_{\rho ^4}\leq \mathfrak {r}_{\rho ^8}\leq \cdots $
. There is an n such that
$\mathfrak {r}_{\rho }\leq \mathfrak {r}_{\rho ^2}\leq \mathfrak {r}_{\rho ^4}\leq \mathfrak {r}_{\rho ^8}\leq \cdots $
. There is an n such that
![]() (because
(because
![]() ), and hence
), and hence
![]() .
.
Note that we did not make use of Tukey connections in the proof above. Therefore, the dual equality of
![]() $\rho $
-splitting numbers for different parameters
$\rho $
-splitting numbers for different parameters
![]() $\rho $
does not follow. In fact, we only showed that a family too small to be
$\rho $
does not follow. In fact, we only showed that a family too small to be
![]() -reaping is not
-reaping is not
![]() $\rho $
-reaping and vice versa—which does not, in any obvious way, yield a method to turn a
$\rho $
-reaping and vice versa—which does not, in any obvious way, yield a method to turn a
![]() -reaping family into a
-reaping family into a
![]() $\rho $
-reaping family or vice versa.
$\rho $
-reaping family or vice versa.
Question D. Is it consistent that
![]() $\mathfrak {s}_{\rho }\ne \mathfrak {s}_{\tau }$
for some
$\mathfrak {s}_{\rho }\ne \mathfrak {s}_{\tau }$
for some
![]() $\rho ,\tau \in (0,1)$
?
$\rho ,\tau \in (0,1)$
?
The next natural question is if we can generalise
![]() , that is, the inequalities
, that is, the inequalities
![]() and
and
![]() for arbitrary
for arbitrary
![]() $\rho \in (0,1)$
.
$\rho \in (0,1)$
.
![]() $\mathbf {Cov}(\mathcal {N})\preccurlyeq \mathbf {Reap}_{\rho }$
is problematic because in the case of
$\mathbf {Cov}(\mathcal {N})\preccurlyeq \mathbf {Reap}_{\rho }$
is problematic because in the case of
![]() , the proof uses the law of large numbers to show that
, the proof uses the law of large numbers to show that
![]() is of measure
is of measure
![]() $1$
for every fixed
$1$
for every fixed
![]() $R\in [\omega ]^{\omega }$
.
$R\in [\omega ]^{\omega }$
.
Question E. Does
![]() $\mathbf {Cov}(\mathcal {N})\preccurlyeq \mathbf {Reap}_{\rho }$
, or at least
$\mathbf {Cov}(\mathcal {N})\preccurlyeq \mathbf {Reap}_{\rho }$
, or at least
![]() $\mathrm {non}(\mathcal {N})\geq \mathfrak {s}_{\rho }$
and
$\mathrm {non}(\mathcal {N})\geq \mathfrak {s}_{\rho }$
and
![]() $\mathrm {cov}(\mathcal {N})\leq \mathfrak {r}_{\rho }$
, hold?
$\mathrm {cov}(\mathcal {N})\leq \mathfrak {r}_{\rho }$
, hold?
However,
![]() $\mathbf {Reap}_{\rho }\preccurlyeq \mathbf {Cov}(\mathcal {M})^{\perp }$
and hence
$\mathbf {Reap}_{\rho }\preccurlyeq \mathbf {Cov}(\mathcal {M})^{\perp }$
and hence
![]() $\mathfrak {s}_{\rho }\geq \mathrm {cov}(\mathcal {M})$
and
$\mathfrak {s}_{\rho }\geq \mathrm {cov}(\mathcal {M})$
and
![]() $\mathfrak {r}_{\rho }\leq \mathrm {non}(\mathcal {M})$
hold because it is easy to see that
$\mathfrak {r}_{\rho }\leq \mathrm {non}(\mathcal {M})$
hold because it is easy to see that
![]() $\{X\in [\omega ]^{\omega } \mid S\mid _{\rho } X\}=$
$\{X\in [\omega ]^{\omega } \mid S\mid _{\rho } X\}=$
and hence, identifying
![]() $\mathcal {P}(\omega )$
and
$\mathcal {P}(\omega )$
and
![]() $2^{\omega }$
,
$2^{\omega }$
,
![]() with
with
![]() $F(S)=[\omega ]^{<\omega }\cup \{X\in [\omega ]^{\omega } \mid S\mid _{\rho } X\}$
and
$F(S)=[\omega ]^{<\omega }\cup \{X\in [\omega ]^{\omega } \mid S\mid _{\rho } X\}$
and
![]() $G(X)=X$
if X is infinite and
$G(X)=X$
if X is infinite and
![]() $G(X)=\omega $
if X is finite is a (Borel) Tukey connection.
$G(X)=\omega $
if X is finite is a (Borel) Tukey connection.
We can define
![]() $\mathfrak {s}_0$
,
$\mathfrak {s}_0$
,
![]() $\mathfrak {r}_0$
,
$\mathfrak {r}_0$
,
![]() $\mathfrak {s}_1$
, and
$\mathfrak {s}_1$
, and
![]() $\mathfrak {r}_1$
as well. To avoid the trivial case
$\mathfrak {r}_1$
as well. To avoid the trivial case
![]() $\mathfrak {s}_1=1$
and to maintain the duality
$\mathfrak {s}_1=1$
and to maintain the duality
![]() $\mathfrak {s}_1=\mathfrak {s}_0$
and
$\mathfrak {s}_1=\mathfrak {s}_0$
and
![]() $\mathfrak {r}_1=\mathfrak {r}_0$
, we say that
$\mathfrak {r}_1=\mathfrak {r}_0$
, we say that
![]() $S\mid _0 R$
(“
$S\mid _0 R$
(“
![]() $S \ 0$
-splits R”) if S is infinite and coinfinite, R is infinite, and
$S \ 0$
-splits R”) if S is infinite and coinfinite, R is infinite, and
![]() $|S\cap R\cap n|/|R\cap n|\to 0$
; we define
$|S\cap R\cap n|/|R\cap n|\to 0$
; we define
![]() $S\mid _1 R$
similarly. Hence let
$S\mid _1 R$
similarly. Hence let
![]() $\mathbf {Reap}_0=(\{S\in [\omega ]^{\omega } \mid |\omega \smallsetminus S|=\omega \},\mid _0,[\omega ]^{\omega })$
,
$\mathbf {Reap}_0=(\{S\in [\omega ]^{\omega } \mid |\omega \smallsetminus S|=\omega \},\mid _0,[\omega ]^{\omega })$
,
![]() $\mathbf {Reap}_1=(\{S\in [\omega ]^{\omega } \mid |\omega \smallsetminus S|=\omega \},\mid _1,[\omega ]^{\omega })$
,
$\mathbf {Reap}_1=(\{S\in [\omega ]^{\omega } \mid |\omega \smallsetminus S|=\omega \},\mid _1,[\omega ]^{\omega })$
,
![]() $\mathfrak {s}_0=\mathfrak {b}(\mathbf {Reap}_0)=\mathfrak {s}_1=\mathfrak {b}(\mathbf {Reap}_1)$
, and
$\mathfrak {s}_0=\mathfrak {b}(\mathbf {Reap}_0)=\mathfrak {s}_1=\mathfrak {b}(\mathbf {Reap}_1)$
, and
![]() $\mathfrak {r}_0=\mathfrak {d}(\mathbf {Reap}_0)=\mathfrak {r}_1=\mathfrak {d}(\mathbf {Reap}_1)$
.
$\mathfrak {r}_0=\mathfrak {d}(\mathbf {Reap}_0)=\mathfrak {r}_1=\mathfrak {d}(\mathbf {Reap}_1)$
.
Just like for
![]() $\rho \in (0,1)$
, if
$\rho \in (0,1)$
, if
![]() $S\in [\omega ]^{\omega }$
and
$S\in [\omega ]^{\omega }$
and
![]() $|\omega \smallsetminus S|=\omega $
, then
$|\omega \smallsetminus S|=\omega $
, then
![]() $\{X\in [\omega ]^{\omega } \mid S\mid _0X\}\in \mathcal {M}$
and hence
$\{X\in [\omega ]^{\omega } \mid S\mid _0X\}\in \mathcal {M}$
and hence
![]() $\mathbf {Reap}_0\preccurlyeq \mathbf {Cov}(\mathcal {M})^{\perp }$
; in particular,
$\mathbf {Reap}_0\preccurlyeq \mathbf {Cov}(\mathcal {M})^{\perp }$
; in particular,
![]() $\mathfrak {s}_0\geq \mathrm {cov}(\mathcal {M})$
and
$\mathfrak {s}_0\geq \mathrm {cov}(\mathcal {M})$
and
![]() $\mathfrak {r}_0\leq \mathrm {non}(\mathcal {M})$
.
$\mathfrak {r}_0\leq \mathrm {non}(\mathcal {M})$
.
Fact 5.4.
![]() $\mathbf {Dom}^{\perp }\preccurlyeq \mathbf {Reap}_0$
and hence
$\mathbf {Dom}^{\perp }\preccurlyeq \mathbf {Reap}_0$
and hence
![]() $\mathfrak {d}\geq \mathfrak {s}_0$
and
$\mathfrak {d}\geq \mathfrak {s}_0$
and
![]() $\mathfrak {b}\leq \mathfrak {r}_0$
.
$\mathfrak {b}\leq \mathfrak {r}_0$
.
Proof Instead of
![]() $\omega ^{\omega }$
, we work with
$\omega ^{\omega }$
, we work with
![]() $\mathcal {X}=\{x\in \omega ^{\uparrow \omega } \mid |\omega \smallsetminus \mathrm {ran}(x)|=\omega \}$
. It is trivial to show that
$\mathcal {X}=\{x\in \omega ^{\uparrow \omega } \mid |\omega \smallsetminus \mathrm {ran}(x)|=\omega \}$
. It is trivial to show that
![]() $(\mathcal {X},\leq ^*,\mathcal {X})\equiv (\omega ^{\omega },\leq ^*,\omega ^{\omega })=\mathbf {Dom}$
. We define a Tukey connection
$(\mathcal {X},\leq ^*,\mathcal {X})\equiv (\omega ^{\omega },\leq ^*,\omega ^{\omega })=\mathbf {Dom}$
. We define a Tukey connection
![]() $(F,G)\colon \mathbf {Reap}_0^{\perp }\to \mathbf {Dom}$
, that is, an
$(F,G)\colon \mathbf {Reap}_0^{\perp }\to \mathbf {Dom}$
, that is, an
as follows: Let
![]() $F\colon [\omega ]^{\omega }\to \mathcal {X}$
be defined by
$F\colon [\omega ]^{\omega }\to \mathcal {X}$
be defined by
![]() $F(R)(n)=r_{2^n}$
where
$F(R)(n)=r_{2^n}$
where
![]() $R=\{r_0<r_1<\cdots \}\in [\omega ]^{\omega }$
and let
$R=\{r_0<r_1<\cdots \}\in [\omega ]^{\omega }$
and let
![]() $G\colon \mathcal {X}\to \{S\in [\omega ]^{\omega } \mid |\omega \smallsetminus S|=\omega \}$
be defined by
$G\colon \mathcal {X}\to \{S\in [\omega ]^{\omega } \mid |\omega \smallsetminus S|=\omega \}$
be defined by
![]() $G(x)=\mathrm {ran}(x)$
. If
$G(x)=\mathrm {ran}(x)$
. If
![]() $F(R)\leq ^* x$
,
$F(R)\leq ^* x$
,
![]() $r_{2^n}\leq x(n)$
for every
$r_{2^n}\leq x(n)$
for every
![]() $n\geq N$
for some N and
$n\geq N$
for some N and
![]() $r_{2^n}<k\leq r_{2^{n+1}}$
, then
$r_{2^n}<k\leq r_{2^{n+1}}$
, then
 $$ \begin{align*} \frac{|\mathrm{ran}(x)\cap R\cap k|}{|R\cap k|}\leq \frac{N+n}{2^n}\xrightarrow{n\to\infty} 0\text{,} \end{align*} $$
$$ \begin{align*} \frac{|\mathrm{ran}(x)\cap R\cap k|}{|R\cap k|}\leq \frac{N+n}{2^n}\xrightarrow{n\to\infty} 0\text{,} \end{align*} $$
and hence
![]() $G(x)=\mathrm {ran}(x) \ 0$
-splits R.
$G(x)=\mathrm {ran}(x) \ 0$
-splits R.
Question F. Does
![]() $\mathbf {Dom}^{\perp }\equiv \mathbf {Reap}_0$
, and hence
$\mathbf {Dom}^{\perp }\equiv \mathbf {Reap}_0$
, and hence
![]() $\mathfrak {d}=\mathfrak {s}_0$
and
$\mathfrak {d}=\mathfrak {s}_0$
and
![]() $\mathfrak {b}=\mathfrak {r}_0$
, hold? Or do at least
$\mathfrak {b}=\mathfrak {r}_0$
, hold? Or do at least
![]() $\mathfrak {s}_0\geq \mathfrak {s}$
and
$\mathfrak {s}_0\geq \mathfrak {s}$
and
![]() $\mathfrak {r}_0\leq \mathfrak {r}$
hold?
$\mathfrak {r}_0\leq \mathfrak {r}$
hold?
Funding
The first author was supported by the Austrian Science Fund (FWF) projects P29907 “Borel ideals and filters” and I5918 “Analytic P-ideals, Banach spaces, and measure algebras.”